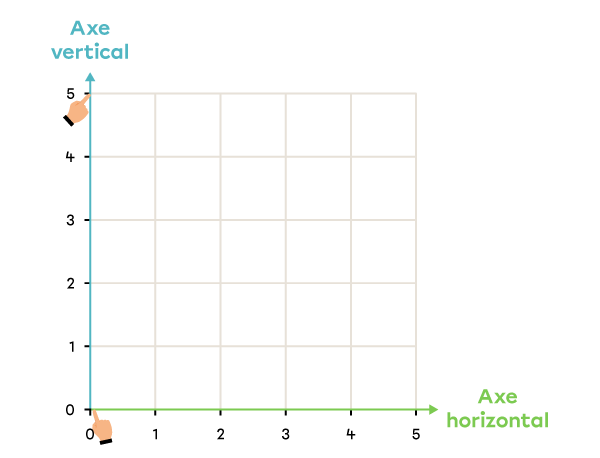
Le plan cartésien est un système de repérage.
Exemple :
Il est formé d’un axe horizontal et d’un axe vertical.
Chaque axe est gradué à l’aide de nombres. L’axe horizontal se lit du 0 vers la droite, et l’axe vertical se lit du 0 vers le haut.
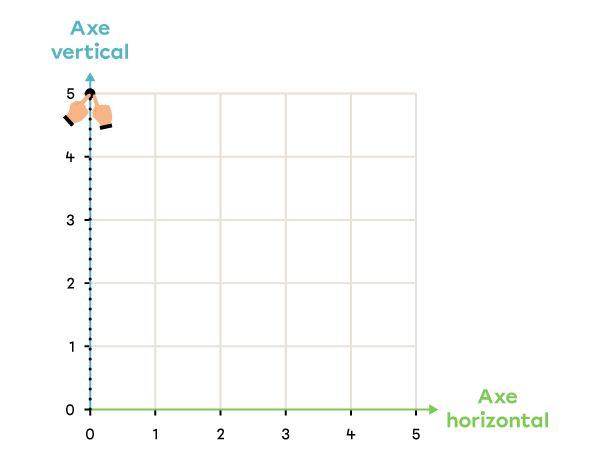
L’axe horizontal se nomme aussi l’axe des x et l’axe vertical, l’axe des y.
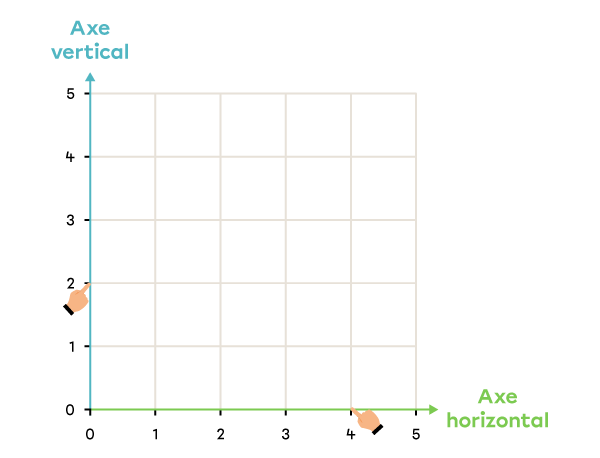
Dans un plan cartésien, chaque point a une position horizontale et une position verticale.
En notant la position horizontale suivie de la position verticale d’un point, on forme un couple qui représente la position exacte du point.
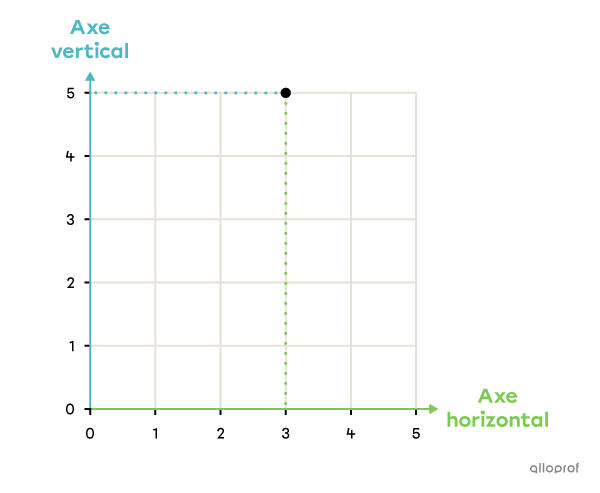
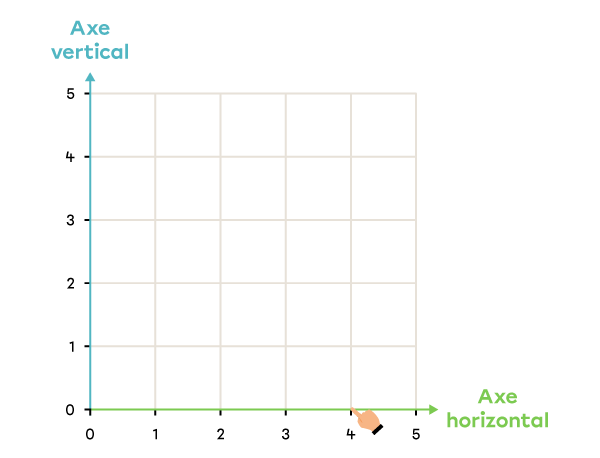
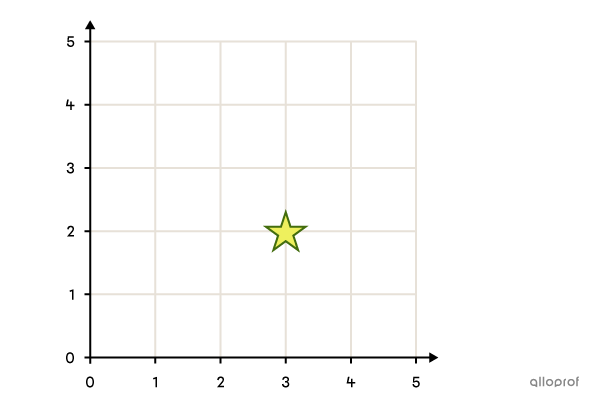
La position horizontale du point est 3.
La position verticale du point est 5.
Le couple (3, 5) représente la position du point.
Il peut aussi y avoir des lettres sur un des axes du plan cartésien. Un couple peut donc être formé d’une lettre et d’un nombre.
Exemple : (B, 6)
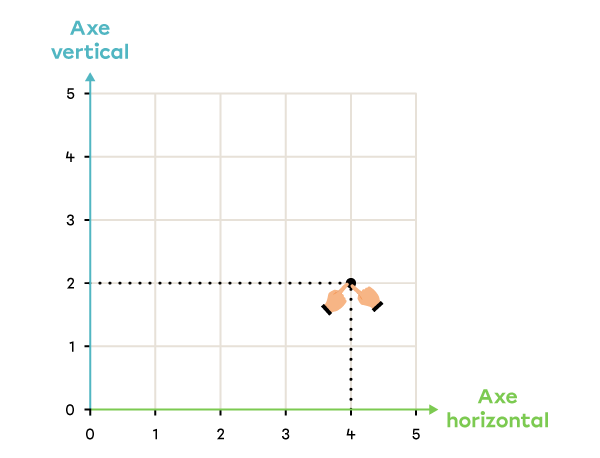
Pour placer un point dans le plan cartésien à partir d’un couple de nombres, je dois suivre les étapes suivantes.
-
Je regarde le premier nombre du couple.
-
Je repère ce nombre sur l’axe horizontal.
-
Je regarde le deuxième nombre du couple.
-
Je repère ce nombre sur l’axe vertical.
-
Je suis les lignes associées à chaque nombre et je place le point à l’endroit où elles se rencontrent.
Dans le plan cartésien, place un point à la position (4, 2).
|
(4, 2) |
|
|
|
(4, 2) |
|
|
|
|
Dans le plan cartésien, place un point à la position (0, 5).
|
(0, 5) |
|
|
|
(0, 5) |
|
|
|
|
Le plan cartésien est un système de repérage.
Exemple :

Le plan cartésien est formé d’un axe horizontal et d’un axe vertical.
Chaque axe est gradué à l’aide de nombres. L’axe horizontal se lit du 0 vers la droite et l’axe vertical se lit du 0 vers le haut.
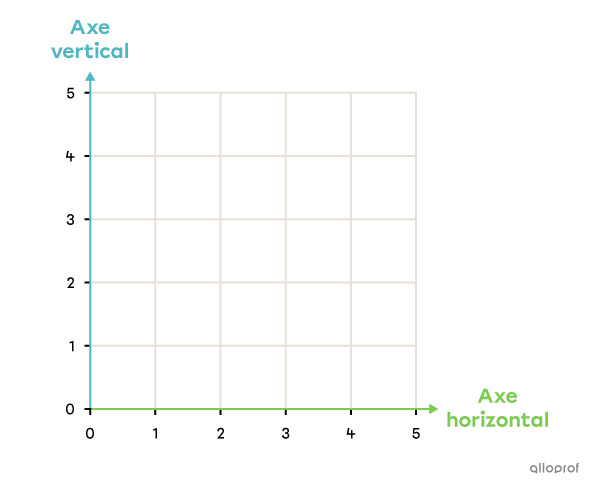
L’axe horizontal se nomme aussi l’axe des x et l’axe vertical, l’axe des y.
Une coordonnée est un nombre qui précise la position horizontale ou verticale d’un point dans le plan cartésien.
La coordonnée horizontale représente la position d’un point sur l’axe horizontal.
La coordonnée verticale représente sa position sur l’axe vertical.

La coordonnée horizontale du point est 3.
La coordonnée verticale du point est 5.
Un couple de nombres sert à noter la position précise d’un point dans un plan cartésien. Il se note en écrivant entre parenthèses la coordonnée horizontale suivie de la coordonnée verticale. Les deux coordonnées sont séparées d’une virgule.

L’origine est le point de croisement de l’axe horizontal et de l’axe vertical. Il est représenté par les coordonnées (0, 0).
Exemple :
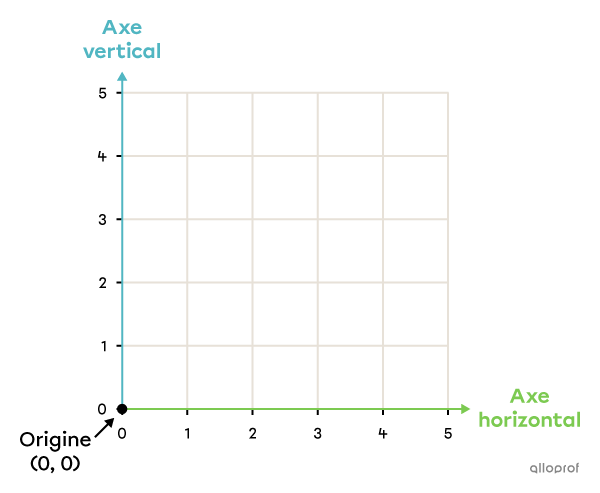
Pour placer un point dans le plan cartésien à partir de ses coordonnées, je dois suivre les étapes suivantes.
-
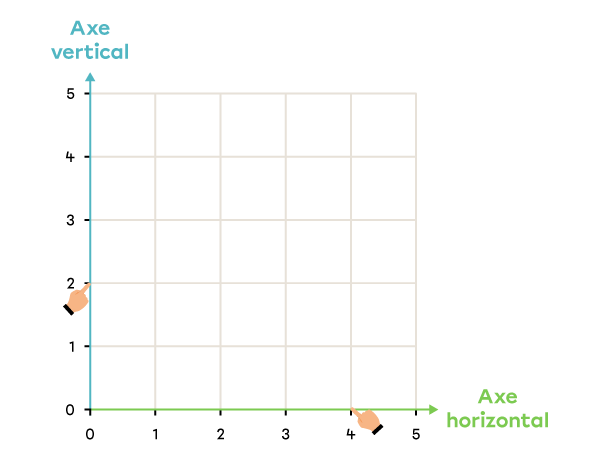
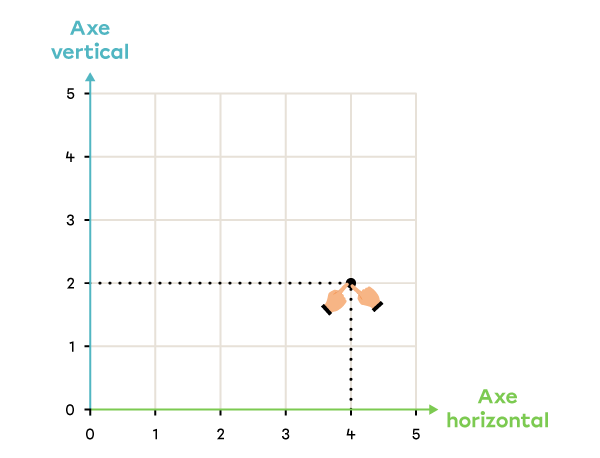
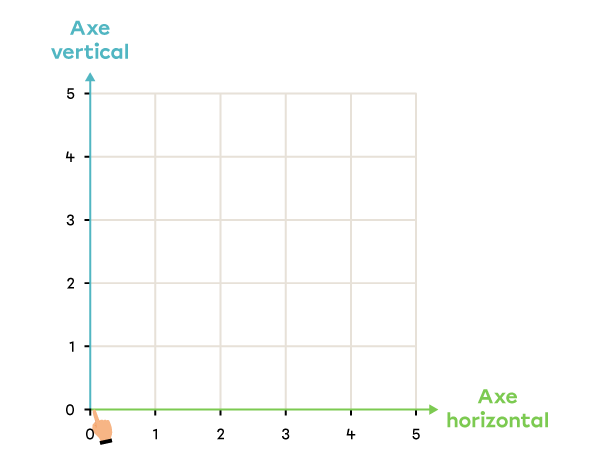
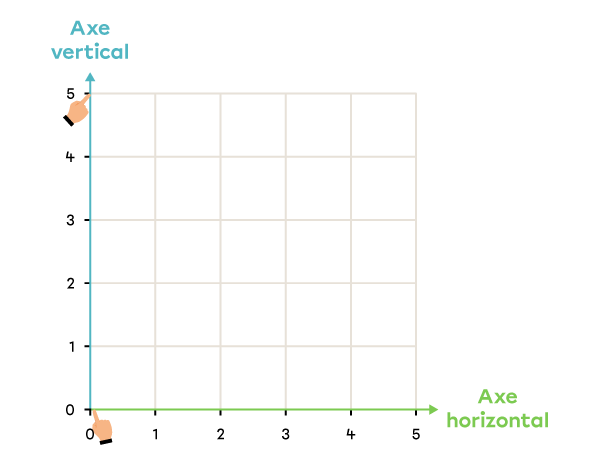
Je regarde la première coordonnée du couple et je repère la ligne vis-à-vis ce nombre sur l’axe horizontal.
-
Je regarde la deuxième coordonnée du couple et je repère la ligne vis-à-vis ce nombre sur l’axe vertical.
-
Je place le point à l’endroit où les deux lignes se rencontrent.
Dans le plan cartésien, place le point ayant les coordonnées (4, 2).
|
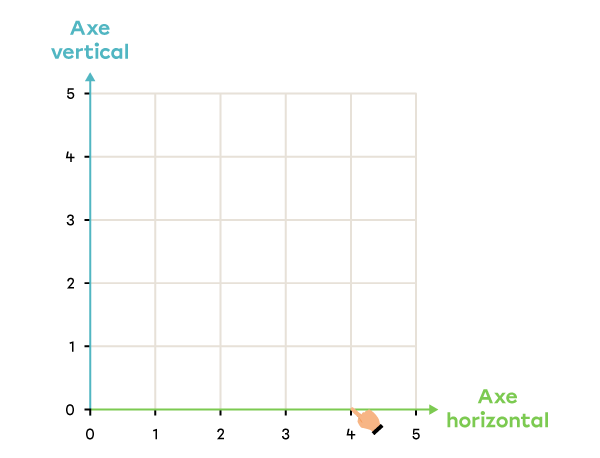 |
|
 |
|
 |
Dans le plan cartésien, place le point ayant les coordonnées (0, 5).
|
 |
|
 |
|
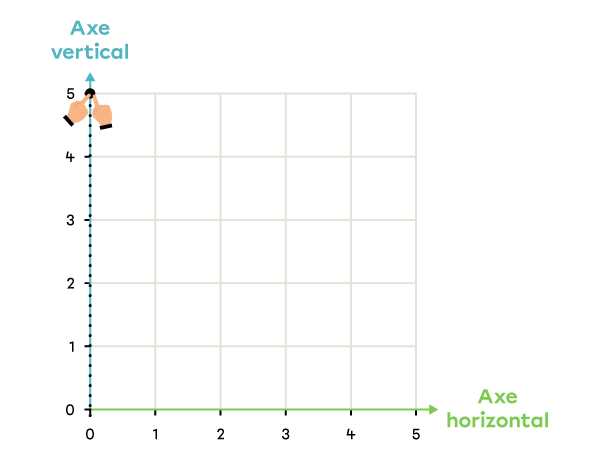 |
Pour noter la position d’un point dans le plan cartésien, je dois suivre les étapes suivantes.
-
Je trouve la coordonnée horizontale du point.
-
Je trouve la coordonnée verticale du point.
-
Je note le couple de nombres en écrivant entre parenthèses la coordonnée horizontale et la coordonnée verticale séparées d’une virgule.
Note la position du point dans le plan cartésien suivant.
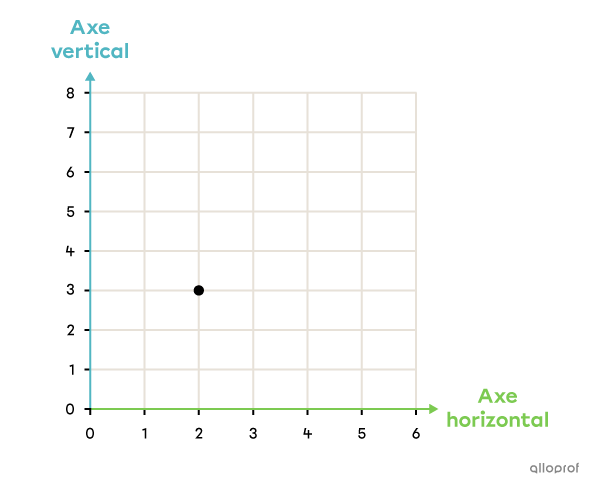
|
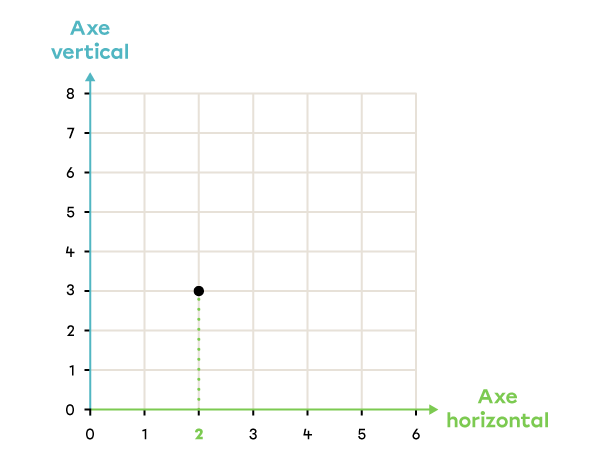 |
|
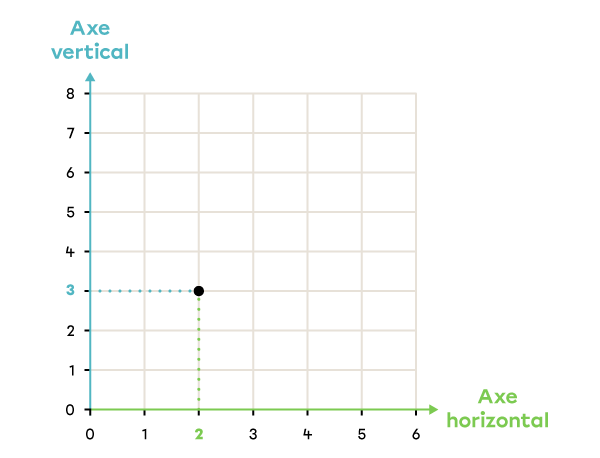 |
|
(2, 3) |
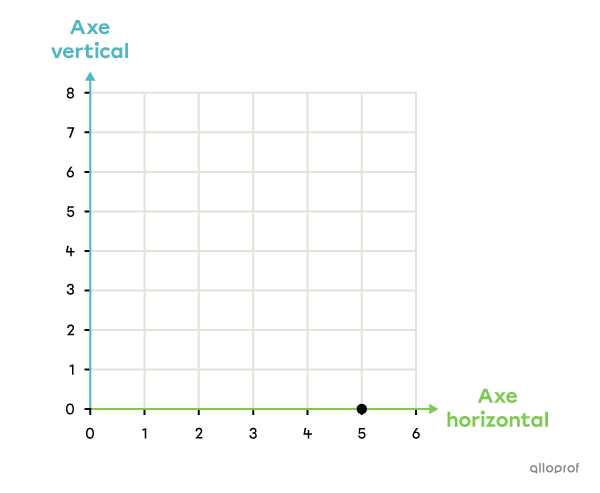
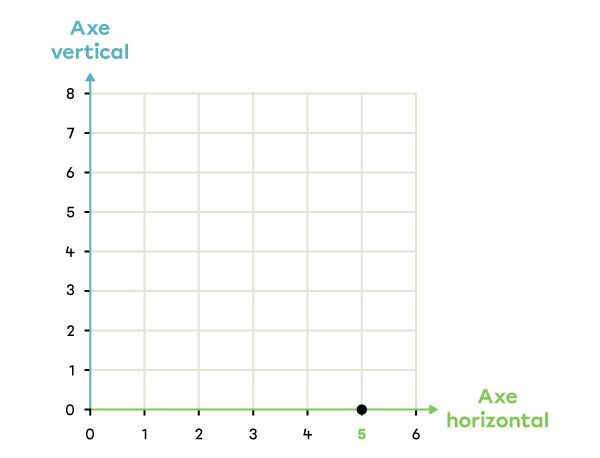
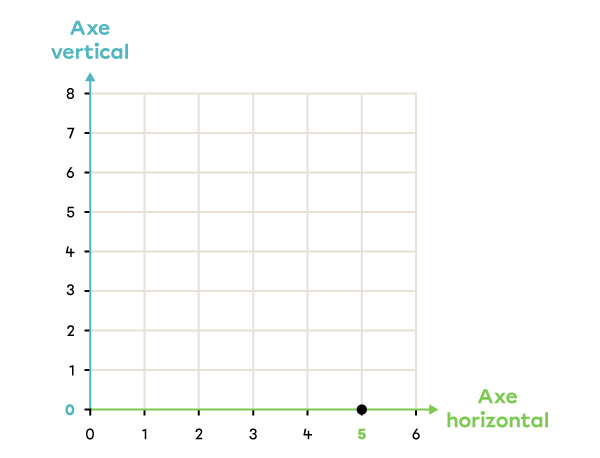
Note la position du point dans le plan cartésien suivant.
|
 |
|
 |
|
(5, 0) |
Le plan cartésien est un système de repérage.
Exemple :

Le plan cartésien est divisé en 4 quadrants séparés par l’axe des x (axe horizontal) et l’axe des y (axe vertical).
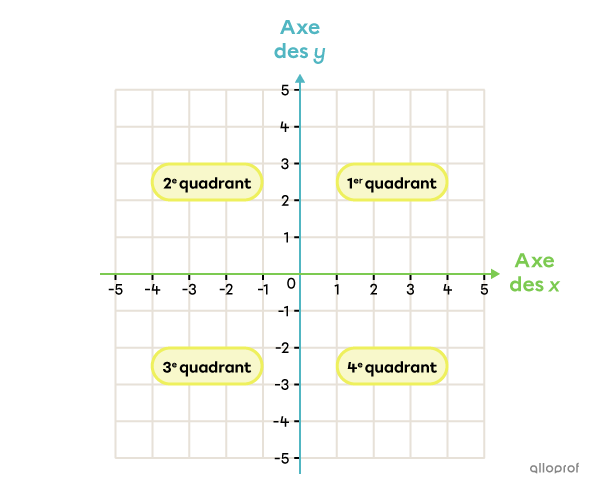
Chaque axe est gradué d’entiers positifs et d’entiers négatifs. Le point central du plan est le 0.
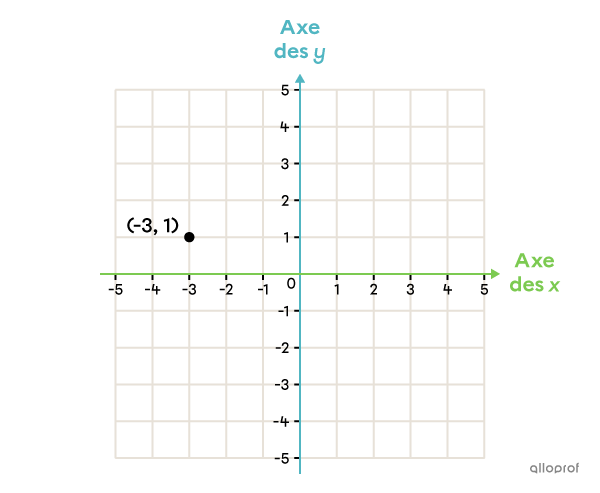
Une coordonnée est un nombre qui précise la position horizontale ou verticale d’un point dans le plan cartésien.
La coordonnée horizontale représente la position d’un point par rapport à l’axe des x (axe horizontal).
La coordonnée verticale représente sa position par rapport à l’axe des y (axe vertical).
La coordonnée horizontale du point est -3.
La coordonnée verticale du point est 1.
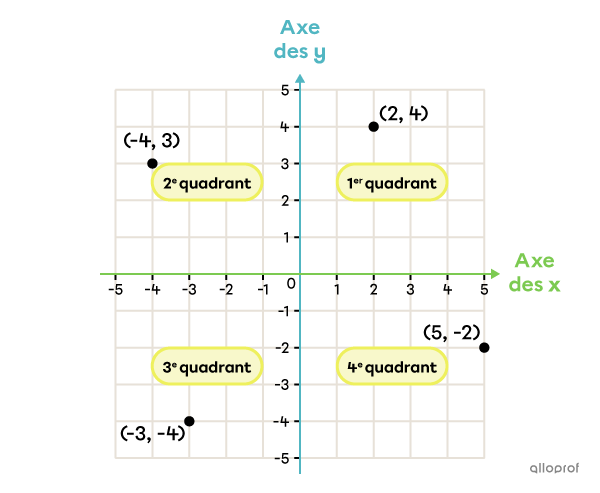
Alors que le plan cartésien à 1 quadrant présente des coordonnées positives, le plan cartésien à 4 quadrants, lui, présente des coordonnées positives et négatives.
Chaque quadrant présente différentes coordonnées positives et/ou négatives.
-
1er quadrant : coordonnée horizontale positive, coordonnée verticale positive.
-
2e quadrant : coordonnée horizontale négative, coordonnée verticale positive.
-
3e quadrant : coordonnée horizontale négative, coordonnée verticale négative.
-
4e quadrant : coordonnée horizontale positive, coordonnée verticale négative.
Exemples :
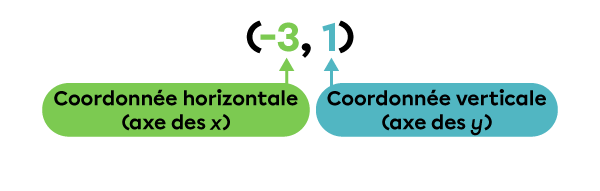
Un couple de nombres sert à noter la position précise d’un point dans un plan cartésien. Il se note en écrivant entre parenthèses la coordonnée horizontale suivie de la coordonnée verticale. Les deux coordonnées sont séparées d’une virgule.
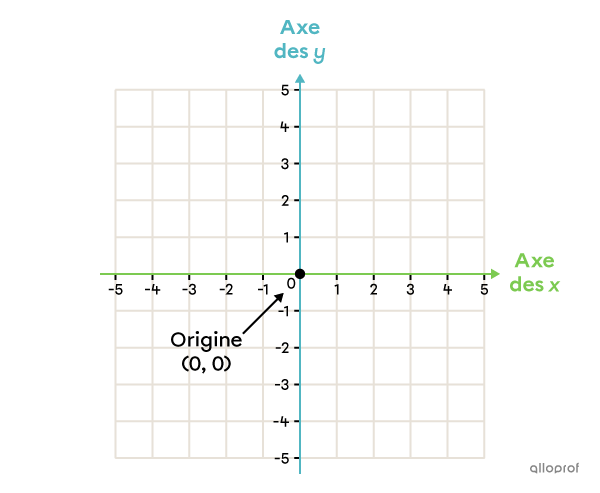
L’origine est le point de croisement de l’axe des x (axe horizontal) et de l’axe des y (axe vertical). Il est représenté par les coordonnées (0, 0).
Exemple :
Pour placer un point dans le plan cartésien à partir de ses coordonnées, je dois suivre les étapes suivantes.
-
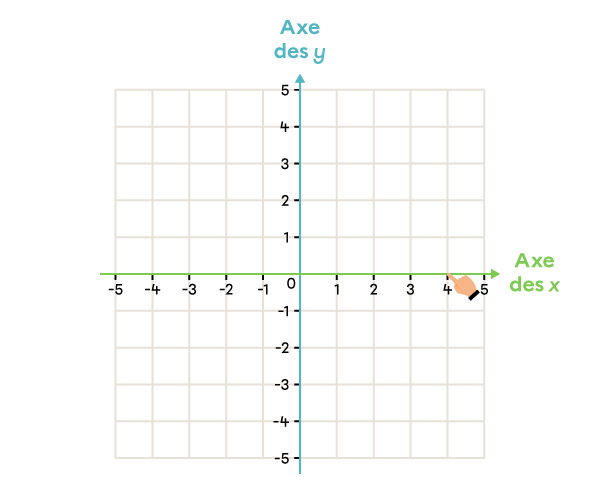
Je regarde la première coordonnée du couple et je repère la ligne vis-à-vis ce nombre sur l’axe horizontal.
-
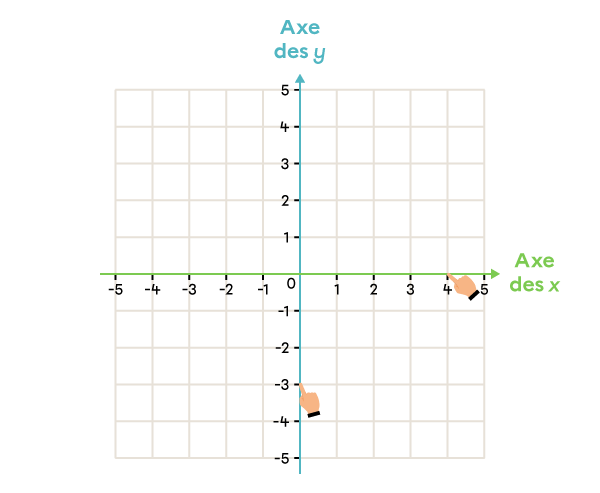
Je regarde la deuxième coordonnée du couple et je repère la ligne vis-à-vis ce nombre sur l’axe vertical.
-
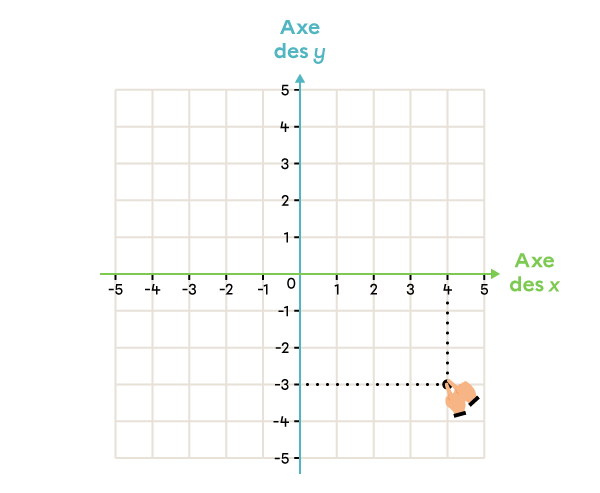
Je place le point à l’endroit où ces deux lignes se rencontrent.
Dans le plan cartésien, place le point ayant les coordonnées (4, -3).
|
 |
|
 |
|
 |
Dans le plan cartésien, place le point ayant les coordonnées (-1, -4).
|
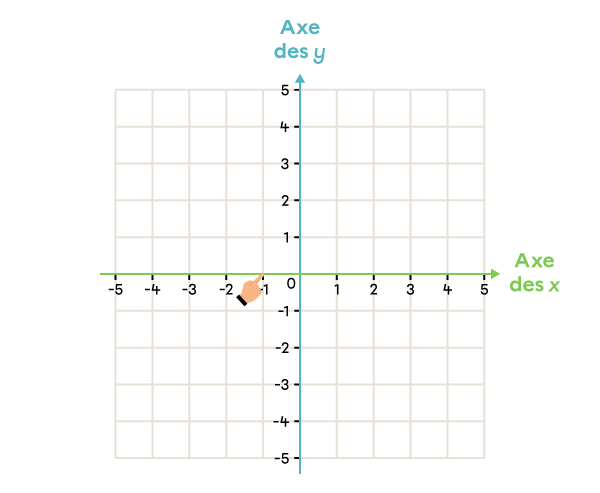 |
|
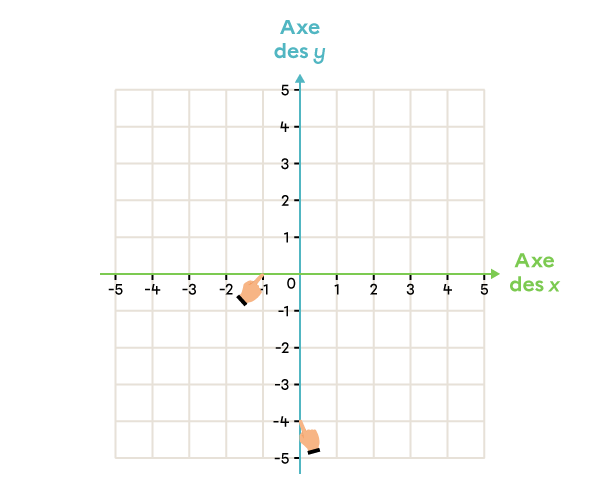 |
|
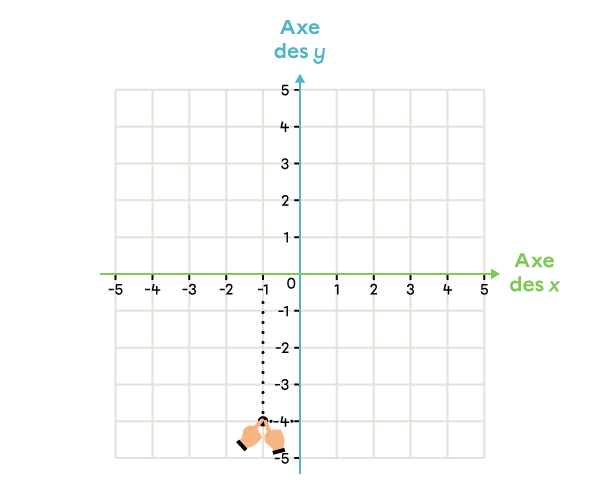 |
Pour noter la position d’un point dans le plan cartésien, je dois suivre les étapes suivantes.
-
Je trouve la coordonnée horizontale du point.
-
Je trouve la coordonnée verticale du point.
-
Je note le couple de nombres en écrivant entre parenthèses la coordonnée horizontale et la coordonnée verticale séparées d’une virgule.
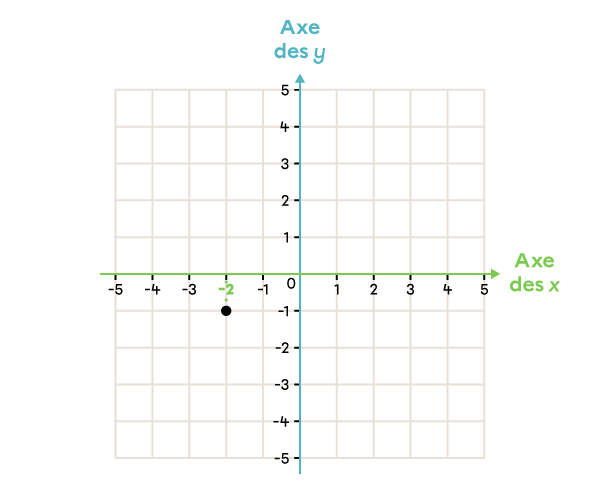
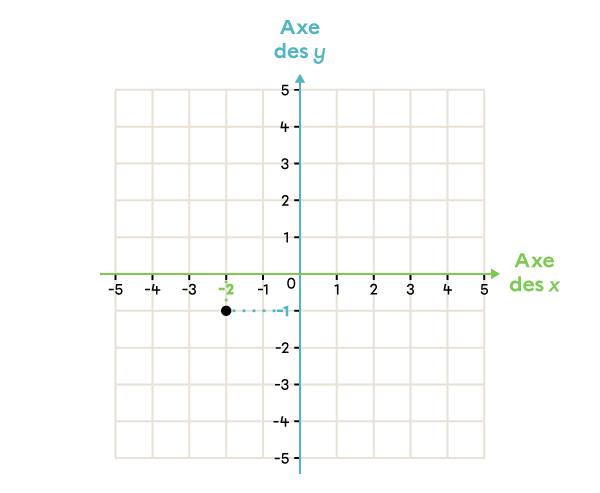
Note la position du point dans le plan cartésien suivant.
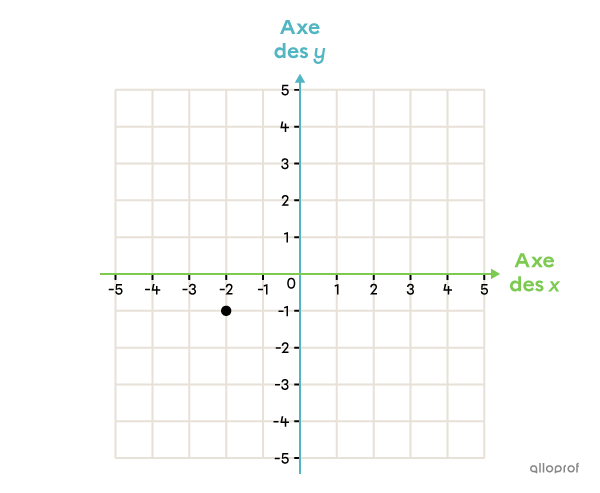
|
 |
|
 |
|
(-2, -1) |
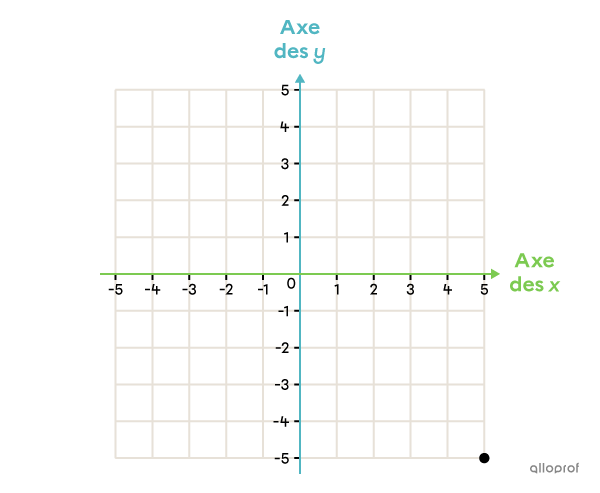
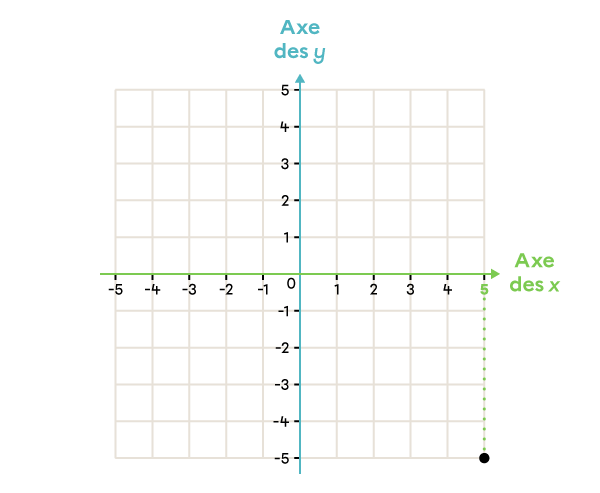
Note la position du point dans le plan cartésien suivant.
|
 |
|
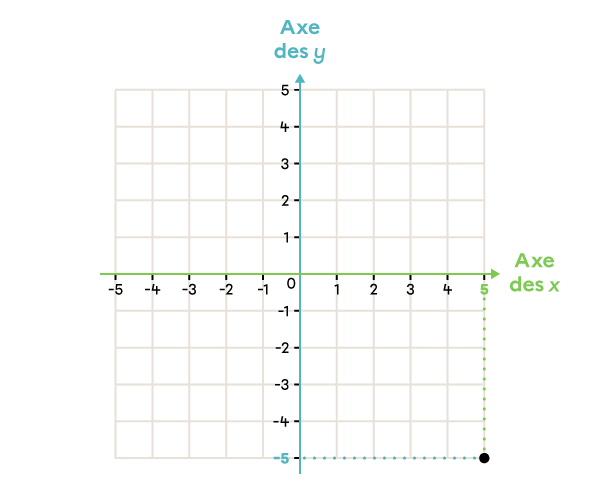 |
|
(5, -5) |