Dans une distribution ordonnée, un rang centile sert de mesure de position et permet de comparer une donnée par rapport aux autres.
-
Le rang centile d’une donnée |x| correspond au pourcentage des données dont la valeur est inférieure ou égale à |x.| On note le rang centile de |x| par |R_{100}(x).|
-
Les centiles correspondent aux |99| valeurs qui séparent une distribution ordonnée en |100| groupes qui contiennent environ |1\ \%| des données. On note les centiles de |C_1| à |C_{99}.|
Les données qui ont la même valeur doivent occuper le même rang centile.
Lorsqu’on cherche le rang centile d’une donnée |x,| on utilise la formule suivante.
||R_{100}(x)=\dfrac{\begin{gather}\text{Nombre de données de}\\\text{valeur inférieure à }x\end{gather}+\dfrac{1}{2}\left(\begin{gathered}\text{Nombre de données de}\\\text{valeur égale à }x\end{gathered}\right)}{\begin{gather}\text{Nombre total de données}\end{gather}}\times100||
Si on obtient un résultat qui n’est pas un nombre naturel, on doit arrondir à l’entier supérieur.
Dans une classe de |30| élèves, Martine a obtenu une note de |83\ \%| au dernier examen de mathématiques, soit la 4e meilleure note du groupe. De plus, elle est la seule élève qui a obtenu ce résultat.
Quel est le rang centile de Martine?
Selon les informations fournies, |26| élèves |(30-4)| ont obtenus un résultat inférieur à |83\ \%.| De plus, |1| seul élève (Martine) a obtenu exactement |83\ \%.|
On calcule le rang centile de Martine à l’aide de la formule.||\begin{align}R_{100}(\text{Martine})&=\dfrac{\begin{gather}\text{Nombre de notes}\\\text{inférieures à }83\ \%\end{gather}+\dfrac{1}{2}\left(\begin{gathered}\text{Nombre de notes}\\\text{égales à }83\ \%\end{gathered}\right)}{\begin{gather}\text{Nombre total de notes}\end{gather}}\times100\\&=\dfrac{26+\dfrac{1}{2}(1)}{30}\times100\\&=88{,}\overline{3}\end{align}||En arrondissant à l’entier supérieur, on obtient |89.|
Réponse : Martine occupe le 89e rang centile, qu’on note |R_{100}(\text{Martine})=89.|
Il faut toujours prendre en compte le contexte d’une situation lorsqu’on s’intéresse au rang centile d’une donnée. En effet, plus la donnée étudiée est meilleure ou performante par rapport aux autres données, plus son rang centile est élevé.
Dans l’exemple précédent, les élèves sont classés en fonction de leur note sur |100.| Ainsi, plus la note d’un élève est élevée, plus l’élève est performant, donc plus son rang centile est élevé.
À l’inverse, on pourrait s’intéresser aux participants à une course, où les participants sont classés en fonction du temps qu’ils ont pris pour parcourir la distance. Dans ce genre de situation, plus le temps d’un participant est petit, plus le participant est performant, donc plus son rang centile est élevé.
Lors du dernier grand tour du Lac Mégantic en vélo, il y avait |312| participants. Dany a franchi la ligne d’arrivé en même temps que |5| autres personnes et ils se sont donc partagé la 89e position au classement.
Quel est le rang centile de Dany?
Selon les informations fournies, |218| cyclistes |(312-88-5-1)| ont franchi la ligne d'arrivée après Dany. En effet, des |312| cyclistes, on doit soustraire les |88| qui sont arrivés avant Dany, les |5| qui sont arrivés en même temps que lui, ainsi que Dany lui-même.
On calcule le rang centile de Dany à l’aide de la formule.||\begin{align}R_{100}(\text{Dany})&=\dfrac{\begin{gather}\text{Nombre de cyclistes}\\\text{arrivés après la }89^\text{e}\ \text{position}\end{gather}+\dfrac{1}{2}\left(\begin{gathered}\text{Nombre de cyclistes}\\\text{à la }89^\text{e}\ \text{position}\end{gathered}\right)}{\begin{gather}\text{Nombre total de cyclistes}\end{gather}}\times100\\&=\dfrac{218+\dfrac{1}{2}(6)}{312}\times100\\&=70{,}8\overline{3}\end{align}||En arrondissant à l’entier supérieur, on obtient |71.|

Réponse : Dany occupe le 71e rang centile, qu’on note |R_{100}(\text{Dany})=71.|
On a défini le rang centile d’une donnée |x| comme étant le pourcentage des données qui ont une valeur inférieure ou égale à |x.| Alors pourquoi prend-on seulement la moitié des données qui sont égales à |x| dans la formule?||R_{100}(x)=\dfrac{\begin{gather}\text{Nombre de données de}\\\text{valeur inférieure à }x\end{gather}+\color{#ec0000}{\boldsymbol{\dfrac{1}{2}}\left(\color{black}{\begin{gathered}\text{Nombre de données de}\\\text{valeur égale à }x\end{gathered}}\right)}}{\begin{gather}\text{Nombre total de données}\end{gather}}\times100||C’est parce que le rang centile, en tant que mesure de position, est une estimation qui s’applique surtout à des distributions comportant un grand nombre de données.
Si on inclut toutes les données qui ont une valeur égale à |x| dans le calcul, il se peut alors qu’on obtienne un rang centile différent. En effet, dans l’exemple précédent, Dany se serait retrouvé dans le 72e rang centile.||\begin{align}R_{100}(\text{Dany})&=\dfrac{\begin{gather}\text{Nombre de cyclistes}\\\text{arrivés après la }89^\text{e}\ \text{position}\end{gather}+\begin{gathered}\text{Nombre de cyclistes}\\\text{à la }89^\text{e}\ \text{position}\end{gathered}}{\begin{gather}\text{Nombre total de cyclistes}\end{gather}}\times100\\&=\dfrac{218+6}{312}\times100\\&\approx71{,}79\ \rightarrow\ 72\end{align}||
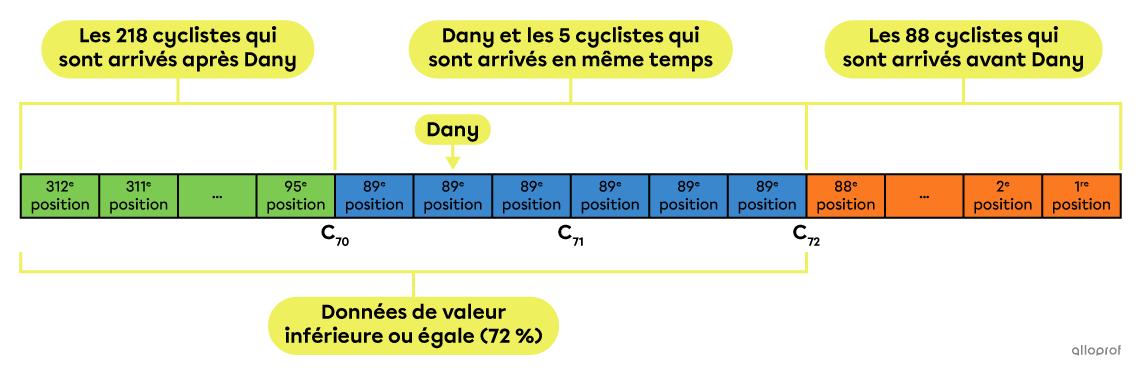
Il arrive aussi qu’on exclue toutes les données qui ont une valeur égale à |x| dans le calcul. Dans ce cas, dans l’exemple précédent, Dany se serait retrouvé dans le 70e rang centile.||\begin{align}R_{100}(\text{Dany})&=\dfrac{\begin{gather}\text{Nombre de cyclistes}\\\text{arrivés après la }89^\text{e}\ \text{position}\end{gather}}{\begin{gather}\text{Nombre total de cyclistes}\end{gather}}\times100\\ &=\dfrac{218}{312}\times100\\&\approx69{,}87\ \rightarrow\ 70\end{align}||

Ceci dit, la formule qui est utilisée le plus souvent dans les écoles secondaires du Québec est celle contenant la fraction |\boldsymbol{\color{#ec0000}{\dfrac{1}{2}}}.|
Il est possible de convertir les rangs centiles en quarts et les centiles en quartiles.
-
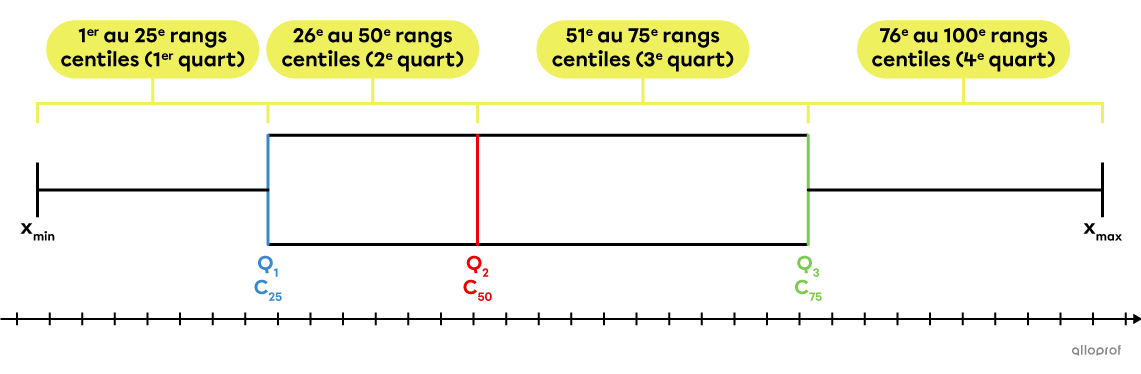
Les rangs centiles 1 à 25 correspondent au 1er quart.
-
Les rangs centiles 26 à 50 correspondent au 2e quart.
-
Les rangs centiles 51 à 75 correspondent au 3e quart.
-
Les rangs centiles 76 à 100 correspondent au 4e quart.
-
Le 25e centile |(C_{25})| correspond au 1er quartile |(Q_1).|
-
Le 50e centile |(C_{50})| correspond à la médiane |(Q_2).|
-
Le 75e centile |(C_{75})| correspond au 3e quartile |(Q_3).|
On peut comparer ces 2 notions à l’aide d’un diagramme de quartiles.
Lorsqu’on cherche la donnée |x| qui occupe un certain rang centile, on doit d’abord calculer sa position dans la distribution à l'aide de la formule suivante.
||\begin{gathered}\text{Position de }x\\\text{dans la distribution}\end{gathered}=\dfrac{R_{100}(x)}{100}\times\begin{gather}\text{Nombre total}\\\text{de données}\end{gather}||
Si on obtient un résultat qui n’est pas un nombre naturel, on doit arrondir à l'entier inférieur.
On a mesuré la taille, en centimètres, des |124| enfants de 15 ans à l’école secondaire de Juliette. Voici la distribution obtenue.||150,155,156,\!\!\!\!\!\!\underbrace{\ldots}_{\large{68\ \text{élèves}}}\!\!\!\!\!,167,167,168,169,170,170,170,171,\!\!\!\!\!\!\underbrace{\ldots}_{\large{42\ \text{élèves}}}\!\!\!\!\!,182,185,188||Quelle est la taille de Juliette si elle se trouve dans le 61e rang centile?
-
Calculer la position de Juliette dans la liste
||\begin{aligned}\begin{gathered}\text{Position de Juliette}\\\text{dans l'école}\end{gathered}&=\dfrac{R_{100}(\text{Juliette})}{100}\times\begin{gather}\text{Nombre total}\\\text{de données}\end{gather}\\&=\dfrac{61}{100}\times124\\&=75{,}64\end{aligned}||En arrondissant à l'entier inférieur, on détermine que Juliette serait la 75e donnée. La position de la donnée recherchée se trouve toujours en comptant à partir de la donnée la moins performante, qui correspond ici à |150.| Ainsi, la 75e donnée est |169.|
-
Valider le résultat
On vérifie si |169| occupe bel et bien le 61e rang centile.||\begin{align}R_{100}(\text{Juliette})&=\dfrac{\begin{gather}\text{Nombre de données}\\\text{inférieures à }169\end{gather}+\dfrac{1}{2}\left(\begin{gathered}\text{Nombre de données}\\\text{égales à }169\end{gathered}\right)}{\begin{gather}\text{Nombre total de données}\end{gather}}\times100\\&=\dfrac{74+\dfrac{1}{2}(1)}{124}\times100\\&\approx60{,}08\end{align}||En arrondissant à l’entier supérieur, on obtient |61.| C’est bel et bien |169| qui correspond à la donnée recherchée.
Réponse : Juliette mesure |169\ \text{cm}.|
Il est toujours préférable de vérifier que le résultat de position obtenu à l’aide de la formule indique une donnée qui occupe bel et bien le rang centile fourni. En effet, il est possible que la donnée recherchée occupe la position suivante dans la distribution.
Dans une classe de |30| élèves, Martine s’est classée au 89e rang centile au dernier examen de mathématiques. De plus, elle est la seule élève qui occupe ce rang. Voici la distribution des résultats de l’examen de tous les élèves de sa classe.
|48,| |50,| |51,| |52,| |54,| |55,| |56,| |58,| |59,| |60,| |62,| |63,| |64,| |66,| |67,| |68,| |70,| |71,| |72,| |74,| |75,| |76,| |78,| |79,| |80,| |82,| |83| |84,| |86,| |87|
Quel a été le résultat de Martine à l’examen de mathématiques?
-
Calculer la position de Martine dans la liste
||\begin{aligned}\begin{gathered}\text{Position de Martine}\\\text{dans le groupe}\end{gathered}&=\dfrac{R_{100}(\text{Martine})}{100}\times\begin{gather}\text{Nombre total}\\\text{de notes}\end{gather}\\&=\dfrac{89}{100}\times30\\&=26{,}7\end{aligned}||En arrondissant à l'entier inférieur, on détermine que Martine serait la 26e donnée |(82)| de la distribution.
-
Valider le résultat
On vérifie si |82| occupe bel et bien le 89e rang centile.||\begin{align}R_{100}(\text{Martine})&=\dfrac{\begin{gather}\text{Nombre de notes}\\\text{inférieures à }82\ \%\end{gather}+\dfrac{1}{2}\left(\begin{gathered}\text{Nombre de notes}\\\text{égales à }82\ \%\end{gathered}\right)}{\begin{gather}\text{Nombre total de notes}\end{gather}}\times100\\&=\dfrac{25+\dfrac{1}{2}(1)}{30}\times100\\&=85\end{align}||Puisque le rang centile de la donnée |82| est |85| et non |89,| ceci implique que |82| n’est pas la donnée recherchée.
-
Calculer le rang centile de la donnée à la position suivante |\boldsymbol{(83)}|
||\begin{align}R_{100}(\text{Martine})&=\dfrac{\begin{gather}\text{Nombre de notes}\\\text{inférieures à }83\ \%\end{gather}+\dfrac{1}{2}\left(\begin{gathered}\text{Nombre de notes}\\\text{égales à }83\ \%\end{gathered}\right)}{\begin{gather}\text{Nombre total de notes}\end{gather}}\times100\\&=\dfrac{26+\dfrac{1}{2}(1)}{30}\times100\\&=88{,}\overline{3}\end{align}||En arrondissant à l’entier supérieur, on obtient |89.| C’est donc |83| qui correspond à la donnée recherchée.
Réponse : Martine a eu un résultat de |83\ \%| au dernier examen de mathématiques.
Pour identifier la position d'une donnée dans une distribution à données condensées, on doit utiliser les effectifs cumulés.
Voici les meilleurs résultats d’un concours d’hommes forts dans lequel les participants devaient soulever un poids de |200\ \text{kg}| le plus longtemps possible.
|
Temps (s) |
Nombre de participants |
Temps (s) |
Nombre de participants |
|---|---|---|---|
|
|8{,}9| |
|10| |
|9{,}6| |
|24| |
|
|9| |
|15| |
|9{,}7| |
|22| |
|
|9{,}1| |
|23| |
|9{,}8| |
|20| |
|
|9{,}2| |
|26| |
|9{,}9| |
|17| |
|
|9{,}3| |
|27| |
|10| |
|10| |
|
|9{,}4| |
|25| |
|10{,}1| |
|5| |
|
|9{,}5| |
|24| |
|10{,}2| |
|2| |
Quelle donnée occupe le 25e rang centile?
-
Calculer la position de la donnée |\boldsymbol{(x)}| dans la liste
||\begin{aligned}\begin{gathered}\text{Position de }x\\\text{dans la distribution}\end{gathered}&=\dfrac{R_{100}(x)}{100}\times\begin{gather}\text{Nombre total}\\\text{de données}\end{gather}\\&=\dfrac{25}{100}\times250\\&=62{,}5\end{aligned}||En arrondissant à l'entier inférieur, on obtient |62.| On doit maintenant déterminer la 62e donnée à l’aide d’un tableau à effectifs cumulés.
|
Temps (s) |
Nombre de participants |
Effectif cumulé |
|---|---|---|
|
|8{,}9| |
|10| |
|10| |
|
|9| |
|15| |
|25| |
|
|9{,}1| |
|23| |
|48| |
|
|9{,}2| |
|26| |
|\boldsymbol{74}| |
|
|9{,}3| |
|27| |
|
|
|9{,}4| |
|25| |
|
|
|9{,}5| |
|24| |
Ainsi, la 62e donnée est associée à un résultat de |9{,}2\ \text{s}.|
-
Valider le résultat
On vérifie si |9{,}2\ \text{s}| occupe bel et bien le 25e rang centile.||\begin{align}R_{100}(9{,}2\ \text{s})&=\dfrac{\begin{gather}\text{Nombre de données}\\\text{inférieures à }9{,}2\ \text{s}\end{gather}+\dfrac{1}{2}\left(\begin{gathered}\text{Nombre de données}\\\text{égales à }9{,}2\ \text{s}\end{gathered}\right)}{\begin{gather}\text{Nombre total de données}\end{gather}}\times100\\&=\dfrac{48+\dfrac{1}{2}(26)}{250}\times100\\&=24{,}4\end{align}||En arrondissant à l’entier supérieur, on obtient |25,| ce qui implique que |9{,}2\ \text{s}| correspond à la donnée recherchée.
Réponse : La donnée qui occupe le 25e rang centile correspond à un résultat de |9{,}2\ \text{s}.|