Le diagramme de quartiles permet d’obtenir d’un seul coup d’œil plusieurs informations à propos de la dispersion des données d’une distribution. Il montre les quartiles (incluant la médiane), la valeur minimale, la valeur maximale, l’étendue interquartile, l’étendue des quarts et les données éloignées. De plus, le diagramme de quartile permet d’évaluer facilement la symétrie (ou l'asymétrie) d’une distribution.
On place généralement un diagramme de quartiles à l’horizontale, mais il est aussi possible qu’il soit placé à la verticale. Voici un exemple de chaque type.
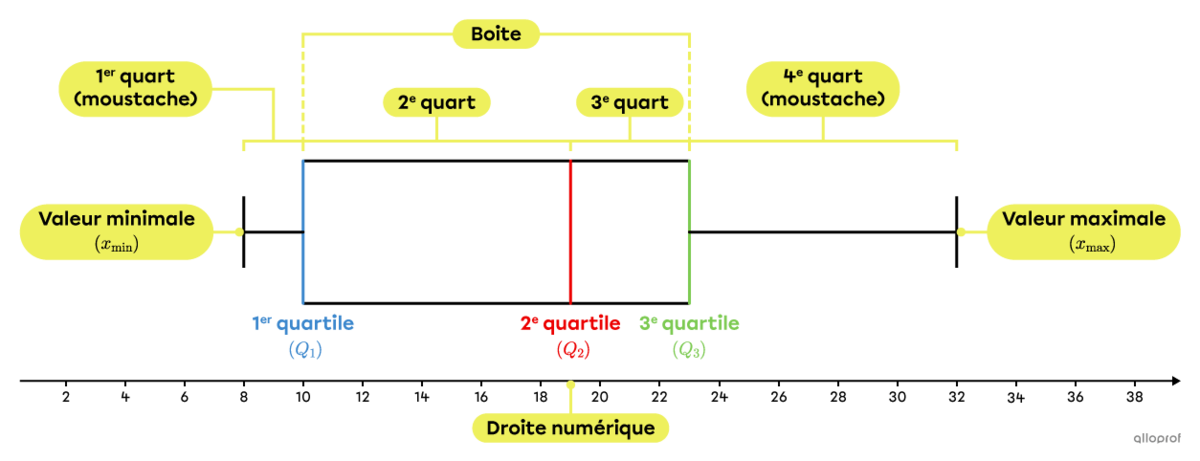
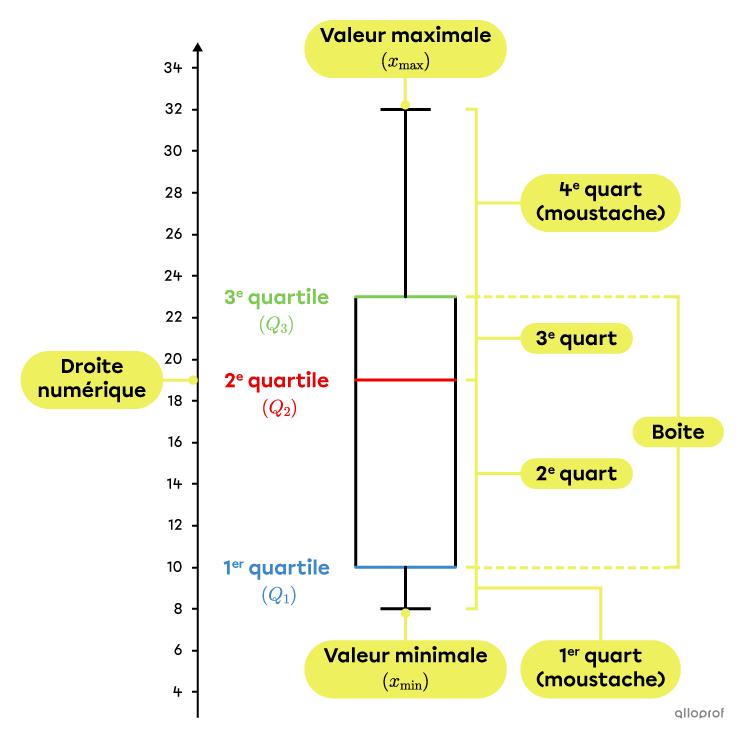
Il peut arriver qu’une distribution contienne quelques données éloignées, c’est-à-dire des données qui ne sont pas représentatives du reste de la distribution. Si de telles données existent, on s’assure qu’elles sont bien indiquées dans le diagramme de quartiles. En effet, on ne peut pas simplement les éliminer, sinon le diagramme serait faussé et perdrait sa crédibilité.
Une donnée éloignée (aberrante) est une valeur de la distribution qui est inférieure à |1{,}5| fois l'étendue interquartile par rapport à |Q_1| ou qui est supérieure à |1{,}5| fois l'étendue interquartile par rapport à |Q_3.|
Autrement dit, une donnée |x| d’une distribution est éloignée si l’une des 2 conditions suivantes est remplie.
-
|x<Q_1-1{,}5\times EI|
-
|x>Q_3+1{,}5\times EI|
Voici la démarche à suivre pour construire un diagramme de quartiles.
-
Placer les données en ordre croissant.
-
Séparer la distribution de données en |4| quarts égaux.
-
Déterminer la valeur des quartiles.
-
Déterminer s'il y a des données éloignées.
-
Déterminer le minimum et le maximum.
-
Tracer le diagramme de quartiles.
Trace le diagramme de quartiles de la distribution suivante.
|15,| |26,| |31,| |16,| |19,| |38,| |12,| |22,| |36,| |27,| |30,| |18,| |29|
-
Placer les données en ordre croissant
|12,| |15,| |16,| |18,| |19,| |22,| |26,| |27,| |29,| |30,| |31,| |36,| |38|
-
Séparer la distribution de données en |\boldsymbol{4}| quarts égaux
Cette distribution est constituée d’un nombre impair de données |(13).| Ainsi, |Q_2| est la donnée au centre de la distribution et la sépare en |2| sous-groupes de |6| données. |Q_1| et |Q_3| sont donc entre des données, de façon à créer |4| quarts qui contiennent |3| données chacun.||\begin{alignat}{20}&&&\boldsymbol{\color{#ec0000}{\underbrace{Q_2}}}\\12,15,16\ &\color{#3b87cd}{\Big\vert}\ 18,19,22\ &&\color{#ec0000}{\boxed{\boldsymbol{26}}}\ 27,29,30\ &&\color{#7cca51}{\Big\vert}\ 31,36,38\\&\!\!\!\!\boldsymbol{\color{#3b87cd}{\overbrace{Q_1}}}&&&&\!\!\!\!\boldsymbol{\color{#7cca51}{\overbrace{Q_3}}}\end{alignat}||
-
Déterminer la valeur des quartiles
On commence par déterminer la valeur de la médiane |(Q_2),| qui correspond à la 7e donnée.||\boldsymbol{\color{#ec0000}{Q_2}}=\boldsymbol{\color{#ec0000}{26}}||Ensuite, on calcule le 1er quartile |(Q_1),| qui correspond au milieu des 3e et 4e données, c’est-à-dire la moyenne.||\begin{alignat}{20}12,15,\boldsymbol{16}\ &\color{#3b87cd}{\Big\vert}\ \boldsymbol{18},19,22\ &&\color{#ec0000}{\boxed{\boldsymbol{26}}}\ 27,29,30\ &&\color{#7cca51}{\Big\vert}\ 31,36,38\\&\!\!\!\!\boldsymbol{\color{#3b87cd}{\overbrace{Q_1}}}\end{alignat}\\\boldsymbol{\color{#3b87cd}{Q_1}}=\dfrac{16+18}{2}=\boldsymbol{\color{#3b87cd}{17}}||Finalement, on calcule le 3e quartile |(Q_3),| qui correspond au milieu des 10e et 11e données.||\begin{alignat}{20}12,15,16\ &\color{#3b87cd}{\Big\vert}\ 18,19,22\ &&\color{#ec0000}{\boxed{\boldsymbol{26}}}\ 27,29,\boldsymbol{30}\ &&\color{#7cca51}{\Big\vert}\ \boldsymbol{31},36,38\\&&&&&\!\!\!\!\boldsymbol{\color{#7cca51}{\overbrace{Q_3}}}\end{alignat}\\\boldsymbol{\color{#7cca51}{Q_3}}=\dfrac{30+31}{2}=\boldsymbol{\color{#7cca51}{30{,}5}}||
-
Déterminer s'il y a des données éloignées
On calcule d'abord l’étendue interquartile.||\begin{align}EI&=Q_3-Q_1\\&=30{,}5–17\\&=13{,}5\end{align}||Ensuite, on vérifie si les données aux extrémités de la distribution sont des données éloignées.
||\begin{align}Q_1-1{,}5\times EI&=17-1{,}5\times13{,}5\\&=-3{,}25\end{align}||Aucune donnée de la distribution n’est inférieure à | –3{,}25.|
||\begin{align}Q_3+1{,}5\times EI&=30{,}5+1{,}5\times13{,}5\\&=50{,}75\end{align}||Aucune donnée de la distribution n’est supérieure à |50{,}75.|
Il n’y a donc aucune donnée éloignée.
-
Déterminer le minimum et le maximum
Puisqu’il n’y a pas de donnée éloignée, la donnée minimale |(x_\text{min})| correspond à la donnée qui a la plus petite valeur et la donnée maximale |(x_\text{max})| correspond à la donnée qui a la plus grande valeur.||\begin{align}x_\text{min}&=12\\x_\text{max}&=38\end{align}||
-
Tracer le diagramme de quartiles
À l’aide d’une droite numérique et des valeurs calculées aux étapes précédentes, on trace le diagramme de quartiles.
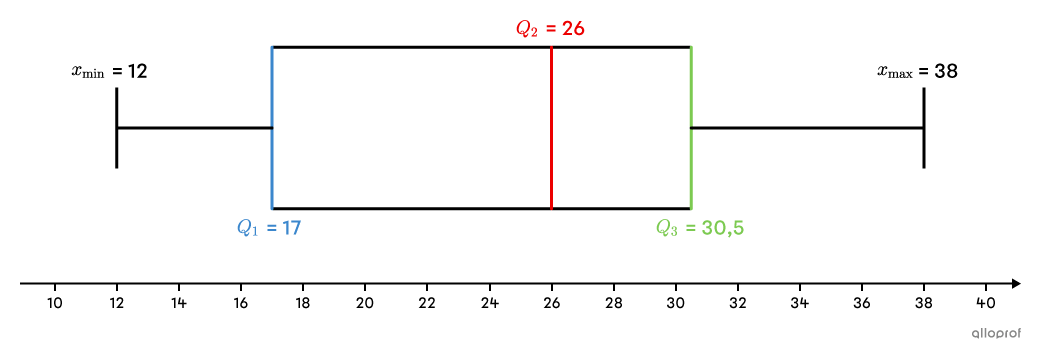
Il n'est pas nécessaire d'indiquer la valeur minimale, la valeur maximale et la valeur des quartiles sur le diagramme, puisqu’il y a toujours une droite numérique.
Voici un exemple d’une distribution dans laquelle on retrouve une donnée éloignée.
Voici les notes obtenues par les élèves du groupe 301 lors d’un examen de mathématiques.
|63,| |96,| |60,| |84,| |52,| |68,| |70,| |12,| |98,| |75,| |72,| |65,| |60,| |74,| |92,| |76,| |94,| |68,| |65,| |88,| |76,| |80|
Trace le diagramme de quartiles de cette distribution.
Voici les notes obtenues par les élèves du groupe 301 lors d’un examen de mathématiques.
|63,| |96,| |60,| |84,| |52,| |68,| |70,| |12,| |98,| |75,| |72,| |65,| |60,| |74,| |92,| |76,| |94,| |68,| |65,| |88,| |76,| |80|
Trace le diagramme de quartiles de cette distribution.
-
Placer les données en ordre croissant
|12,| |52,| |60,| |60,| |63,| |65,| |65,| |68,| |68,| |70,| |72,| |74,| |75,| |76,| |76,| |80,| |84,| |88,| |92,| |94,| |96,| |98|
-
Séparer la distribution de données en |\boldsymbol{4}| quarts égaux
Cette distribution est constituée d’un nombre pair de données |(22).| Ainsi, |Q_2| est entre les |2| données au centre de la distribution et la sépare en |2| sous-groupes de |11| données. |Q_1| et |Q_3| sont donc les données au centre de leur sous-groupe respectif, de façon à créer |4| quarts qui contiennent |5| données chacun.||\begin{alignat}{20}&&&\!\!\!\!\boldsymbol{\color{#ec0000}{\underbrace{Q_2}}}\\12,52,60,60,63\ &\color{#3b87cd}{\boxed{\boldsymbol{65}}}\ 65,68,68,70,72\ &&\color{#ec0000}{\Big\vert}\ 74,75,76,76,80\ &&\color{#7cca51}{\boxed{\boldsymbol{84}}}\ 88,92,94,96,98\\&\!\!\;\boldsymbol{\color{#3b87cd}{\overbrace{Q_1}}}&&&&\!\!\;\boldsymbol{\color{#7cca51}{\overbrace{Q_3}}}\end{alignat}||
-
Déterminer la valeur des quartiles
On commence par déterminer la valeur de la médiane |(Q_2),| qui correspond à la moyenne des 11e et 12e données.||\begin{alignat}{20}&&&\!\!\!\!\boldsymbol{\color{#ec0000}{\underbrace{Q_2}}}\\12,52,60,60,63\ &\color{#3b87cd}{\boxed{\boldsymbol{65}}}\ 65,68,68,70,\boldsymbol{72}\ &&\color{#ec0000}{\Big\vert}\ \boldsymbol{74},75,76,76,80\ &&\color{#7cca51}{\boxed{\boldsymbol{84}}}\ 88,92,94,96,98\\\phantom{\boldsymbol{\overbrace{Q_1}}}\end{alignat}\\\boldsymbol{\color{#ec0000}{Q_2}}=\dfrac{72+74}{2}=\boldsymbol{\color{#ec0000}{73}}||Ensuite, on détermine le 1er quartile |(Q_1),| qui correspond à la 6e donnée.||\boldsymbol{\color{#3b87cd}{Q_1}}=\boldsymbol{\color{#3b87cd}{65}}||Finalement, on détermine le 3e quartile |(Q_3),| qui correspond à la 17e donnée.||\boldsymbol{\color{#7cca51}{Q_3}}=\boldsymbol{\color{#7cca51}{84}}||
-
Déterminer s'il y a des données éloignées
On calcule d'abord l’étendue interquartile.||\begin{align}EI&=Q_3-Q_1\\&=84–65\\&=19\end{align}||Ensuite, on vérifie si les données aux extrémités de la distribution sont des données éloignées.
||\begin{align}Q_1-1{,}5\times EI&=65-1{,}5\times19\\&=36{,}5\end{align}||La 1re donnée de la distribution |(12)| est inférieure à |36{,}5.|
||\begin{align}Q_3+1{,}5\times EI&=84+1{,}5\times19\\&=112{,}5\end{align}||Aucune donnée de la distribution n’est supérieure à | 112{,}5.|
Ainsi, |12| est une donnée éloignée.
-
Déterminer le minimum et le maximum
Puisque |12| est une donnée éloignée, on ne la considère pas comme la valeur minimale de la distribution.||\begin{align}x_\text{min}&=52\\x_\text{max}&=98\end{align}||
-
Tracer le diagramme de quartiles
À l’aide d’une droite numérique et des valeurs calculées aux étapes précédentes, on trace le diagramme de quartiles. On représente la donnée éloignée |(12)| par une étoile.

Il ne faut pas confondre le nombre de données dans un quart avec la concentration des données dans ce même quart.
Chaque quart d’un diagramme de quartiles contient environ |25\ \%| des données de la distribution qu’il représente.
Dans un diagramme de quartiles, un quart plus allongé que les autres indique que les données sont plus dispersées. Inversement, un quart plus court que les autres indique que les données sont plus concentrées.
Dans le but d'ouvrir une nouvelle boutique de vêtements sportifs, on a interrogé un échantillon d'une population pour savoir quel montant d’argent chaque individu était prêt à débourser pour un article de qualité supérieure.
Pour faciliter l'interprétation des données amassées, on construit le diagramme de quartiles suivant.
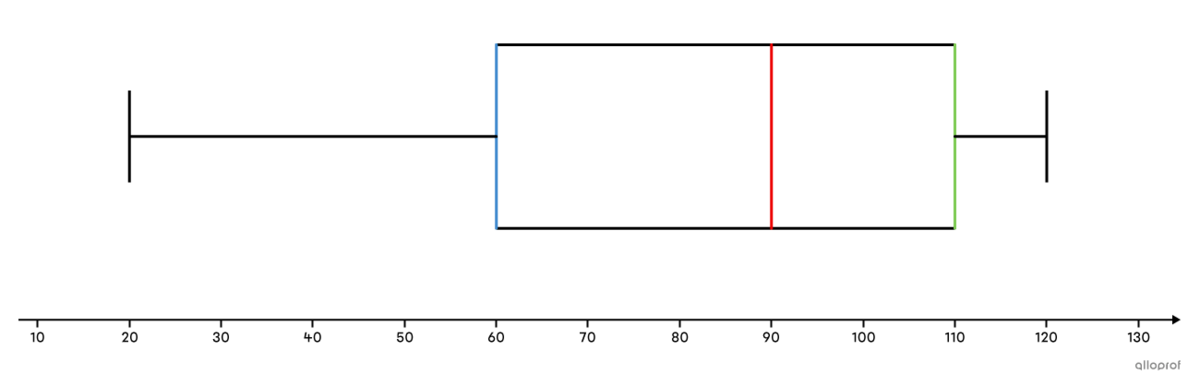
En observant ce diagramme, on peut établir qu’environ |75\ \%| des gens, c’est-à-dire ceux faisant partie des 2e, 3e et 4e quarts, sont prêts à débourser entre |60\ \$| et |120\ \$| pour un article de qualité supérieure.
De plus, on remarque que les personnes du 4e quart sont prêtes à payer un prix dans un intervalle très rapproché (entre |110\ \$| et |120\ \$|), alors que les personnes du 1er quart sont prêtes à débourser un prix dans un intervalle très dispersé (entre |20\ \$| et |60\ \$|).
Ainsi, la future entreprise devra garder ces informations à l’esprit afin de ne pas vendre ses produits trop cher ou pas assez cher.
Il est possible de convertir des quarts en rangs centiles et des quartiles en centiles.
-
Le 1er quart contient les rangs centiles 1 à 25.
-
Le 2e quart contient les rangs centiles 26 à 50.
-
Le 3e quart contient les rangs centiles 51 à 75.
-
Le 4e quart contient les rangs centiles 76 à 100.
-
Le 1er quartile |(Q_1)| correspond au 25e centile |(C_{25}).|
-
La médiane |(Q_2)| correspond au 50e centile |(C_{50}).|
-
Le 3e quartile |(Q_3)| correspond au 75e centile |(C_{75}).|
Lorsqu’on compare des diagrammes de quartiles, on compare d’abord les médianes |(Q_2).| Ensuite, on peut comparer les longueurs des moustaches (1er et 4e quarts) et les longueurs des boites (2e et 3e quarts) pour donner un aperçu de la symétrie et de la dispersion de chaque distribution.
Voici un exemple où on interprète et compare 2 diagrammes de quartiles.
Serge est gérant du département des chaussures d’une boutique d’équipement sportif. Afin de comparer les performances de ses 2 employés, Karine et Éric, il enregistre chaque jour leurs ventes sur une période de 30 jours. À la suite de sa collecte de données, Serge produit les 2 diagrammes de quartiles suivants.
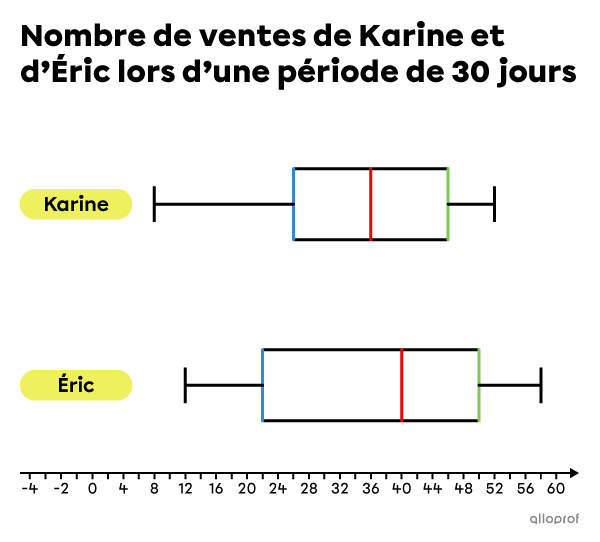
a) Qui a eu le plus petit nombre de ventes en une journée?
b) Quelle est la personne la plus constante dans ses ventes?
c) En considérant leurs |15| meilleures journées respectives, qui a fait le plus de ventes?
d) Est-ce que Karine a nécessairement fait une journée à |36| ventes?
e) Pendant combien de jours Éric a-t-il fait entre |22| et |40| ventes par jour?
Serge est gérant du département des chaussures d’une boutique d’équipement sportif. Afin de comparer les performances de ses 2 employés, Karine et Éric, il enregistre chaque jour leurs ventes sur une période de 30 jours. À la suite de sa collecte de données, Serge produit les 2 diagrammes de quartiles suivants.
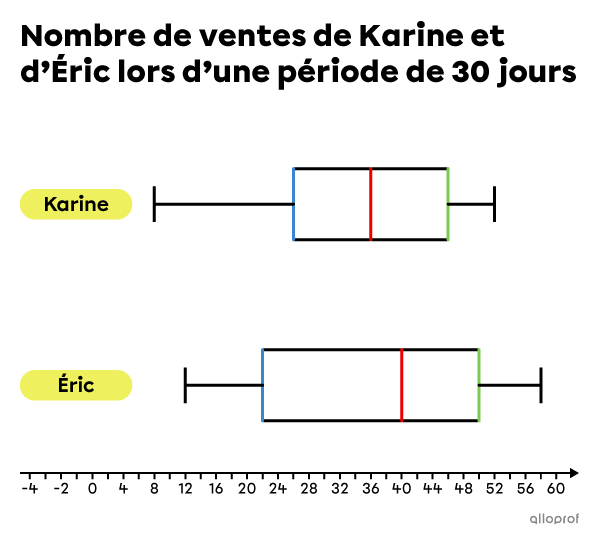
a) Qui a eu le plus petit nombre de ventes en une journée?
b) Quelle est la personne la plus constante dans ses ventes?
c) En considérant leurs |15| meilleures journées respectives, qui a fait le plus de ventes?
d) Est-ce que Karine a nécessairement fait une journée à |36| ventes?
e) Pendant combien de jours Éric a-t-il fait entre |22| et |40| ventes par jour?
a) Qui a eu le plus petit nombre de ventes en une journée?
Il suffit de comparer la donnée minimale |(x_\text{min})| pour Karine et Éric.
Karine||x_\text{min}=8||
Éric||x_\text{min}=12||
Ainsi, la personne qui a eu le plus petit nombre de ventes en une journée est Karine.
b) Quelle est la personne la plus constante dans ses ventes?
On peut comparer l’étendue et l’étendue interquartile |(EI)| pour Karine et Éric, qui donnent une idée de la concentration des données dans chaque distribution.
Karine
La donnée minimale |(x_\text{min})| est |8| et la donnée maximale |(x_\text{max})| est |52.|||\begin{align}\text{Étendue}&=x_\text{max}-x_\text{min}\\&=52-8\\&=44\end{align}||Le 1er quartile |(Q_1)| est |26| et le 3e quartile |(Q_3)| est |46.|||\begin{align}EI&=Q_3-Q_1\\&=46-26\\&=20\end{align}||
Éric
La donnée minimale |(x_\text{min})| est |12| et la donnée maximale |(x_\text{max})| est |58.|||\begin{align}\text{Étendue}&=x_\text{max}-x_\text{min}\\&=58-12\\&=46\end{align}||Le 1er quartile |(Q_1)| est |22| et le 3e quartile |(Q_3)| est |50.|||\begin{align}EI&=Q_3-Q_1\\&=50-22\\&=28\end{align}||
On remarque que l’étendue et l’étendue interquartile des ventes de Karine sont plus petites que celles d’Éric. Autrement dit, comparativement à Éric, les ventes quotidiennes de Karine sont plus concentrées autour de la médiane, ce qui implique que Karine est une vendeuse plus constante qu’Éric.
c) En considérant leurs |\boldsymbol{15}| meilleures journées respectives, qui a fait le plus de ventes?
Pour répondre à cette question, on doit analyser les données. Toutefois, puisqu’on ne les connait pas toutes, on suppose qu’elles sont réparties uniformément dans chaque quart.
Les données de ventes ont été collectées sur une période de |30| jours. On s’intéresse donc à |50\ \%| des jours |\left(\dfrac{15}{30}\right)| au cours desquels Karine et Éric ont fait le plus de ventes. Autrement dit, on doit analyser les 3e et 4e quarts de chaque diagramme de quartiles.
Karine
La médiane |(Q_2)| est |36| et la donnée maximale |(x_\text{max})| est |52.|
Éric
La médiane |(Q_2)| est |40| et la donnée maximale |(x_\text{max})| est |58.|
On remarque que la médiane et la donnée maximale des ventes d’Éric sont toutes les 2 supérieures à celles de Karine. Ainsi, on peut considérer que c’est Éric qui a fait le plus de ventes lors de ses |15| meilleures journées.
d) Est-ce que Karine a nécessairement fait une journée à |\boldsymbol{36}| ventes?
On remarque que |36| correspond à la valeur de la médiane |(Q_2)| de la distribution de Karine. Or, les données ont été collectées sur une période de |30| jours. La médiane correspond donc à la moyenne des 15e et 16e données.||\begin{alignat}{20}&\!\!\!\!\!\!\!\!\!\!\!\boldsymbol{\color{#ec0000}{\underbrace{Q_2=36}}}\\x_\text{min}\ldots15^\text{e}\text{ donnée}\ &\color{#ec0000}{\Big\vert}\ 16^\text{e}\text{ donnée}\ldots x_\text{max}\end{alignat}||Par exemple, la 15e donnée pourrait être |35| et la 16e donnée, |37.| La médiane se calculerait donc de la façon suivante.||\boldsymbol{\color{#ec0000}{Q_2}}=\dfrac{35+37}{2}=36||On en conclut que Karine n’a pas nécessairement fait une journée à 36 ventes.
e) Pendant combien de jours Éric a-t-il fait entre |\boldsymbol{22}| et |\boldsymbol{40}| ventes par jour?
On s’intéresse au nombre de jours dans le 2e quart, c’est-à-dire entre |22| |(Q_1)| et |40| |(Q_2).| On a trouvé précédemment que la médiane |(Q_2)| sépare la distribution en 2 sous-groupes de |15| données. Ceci implique que |Q_1| correspond à la 8e donnée de la distribution.||\begin{alignat}{20}&&&\!\!\!\!\!\!\!\!\!\!\!\boldsymbol{\color{#ec0000}{\underbrace{Q_2=40}}}\\x_\text{min}\ldots7^\text{e}\text{ donnée}\ &\color{#3b87cd}{\boxed{\boldsymbol{8}^\textbf{e}\textbf{ donnée}}}\ 9^\text{e}\text{ donnée}\ldots15^\text{e}\text{ donnée}\ &&\color{#ec0000}{\Big\vert}\ 16^\text{e}\text{ donnée}\ldots x_\text{max}\\&\ \:\boldsymbol{\color{#3b87cd}{\overbrace{Q_1=22}}}\end{alignat}||Chaque quart contient |7| données. Ainsi, à moins que les données |22| et |40| se répètent, on en conclut qu’Éric a fait entre |22| et |40| ventes pendant |7| jours.
Dans l’analyse d’une action à la bourse, on utilise souvent un graphique qui contient un élément semblable à un diagramme de quartile.
Toutefois, il ne faut pas l’interpréter de la même façon, puisque les différentes parties de chaque diagramme ne sont pas des quarts, c’est-à-dire qu’ils ne contiennent pas |25\ \%| des données.
En effet, dans ce genre de diagramme, la longueur de la boite correspond à l’écart entre le prix de l’action à l’ouverture et celui à la fermeture des marchés boursiers.
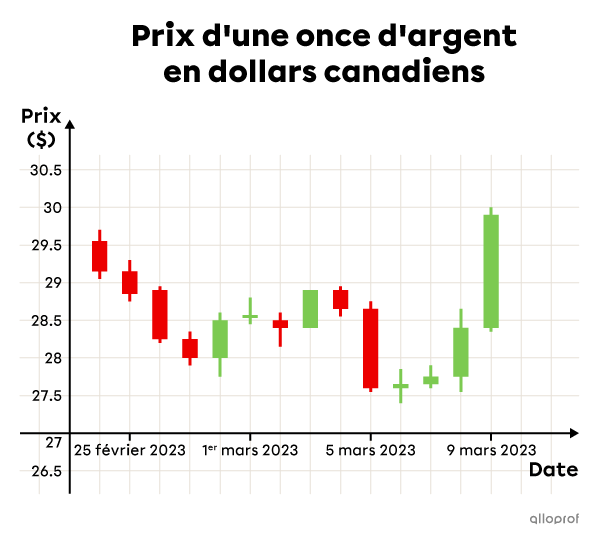
Source des données : OANDA Corporation, 2023
OANDA Corporation. (25 avril 2023). Silver/CAD. https://www.oanda.com/ca-fr/trading/instruments/xag-cad/