Graphiquement, les fonctions périodiques font référence à un modèle qui est reproduit à plusieurs reprises dans le plan cartésien.
Pour bien comprendre le concept de périodicité, il est important de maitriser les concepts de cycle et de période.
On appelle cycle d'une fonction la partie d'un graphique qui correspond à la plus petite portion d'un motif qui se répète.
On appelle période l'écart entre deux abscisses situées aux extrémités d'un même cycle.
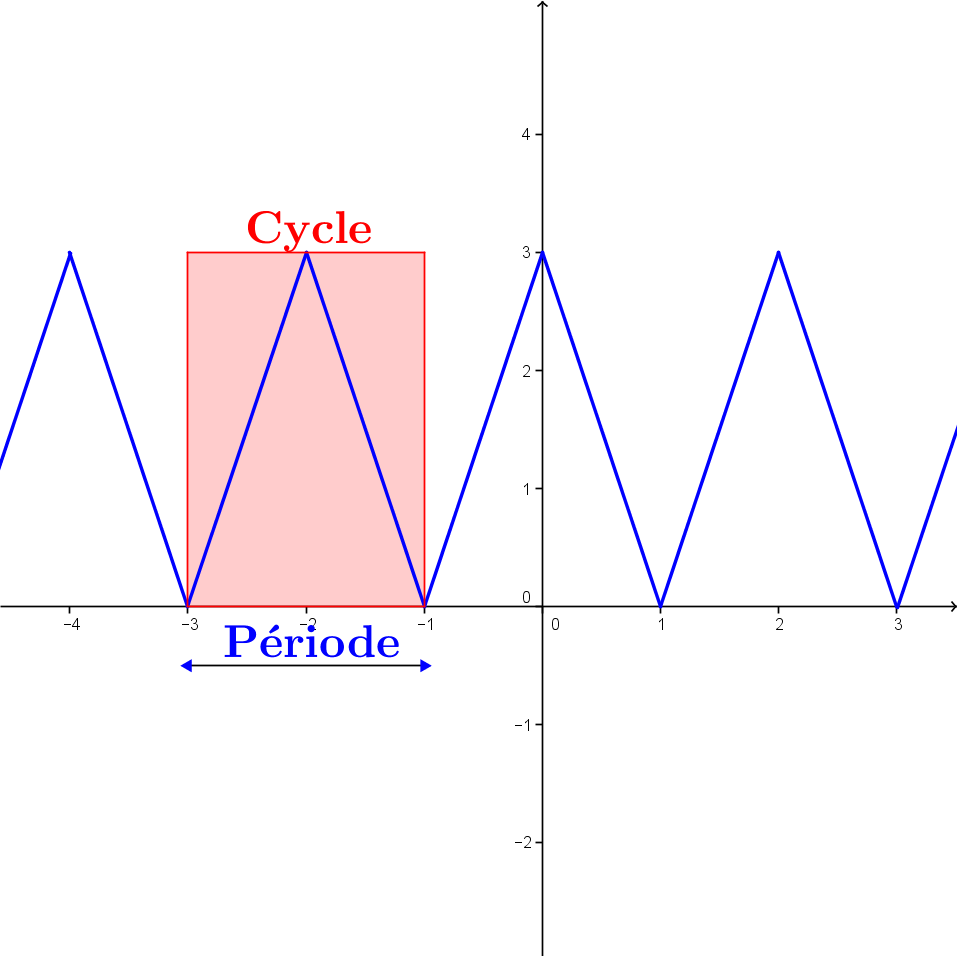
Pour bien illustrer le tout, l'animation suivante présente l'aspect d'une période et la valeur de celle-ci.
Pour résoudre ce genre de problème, il faut absolument commencer la démarche en déterminant le cycle et la période de la fonction périodique.
-
Trouver le cycle et déterminer la période.
-
Utiliser la période pour rapporter le point donné au cycle connu.
-
Trouver l'équation de la droite associée au point donné (si nécessaire)
-
Déterminer la coordonnée manquante.
Dans un contexte de la vie, on pourrait se retrouver face à ce genre de situation.
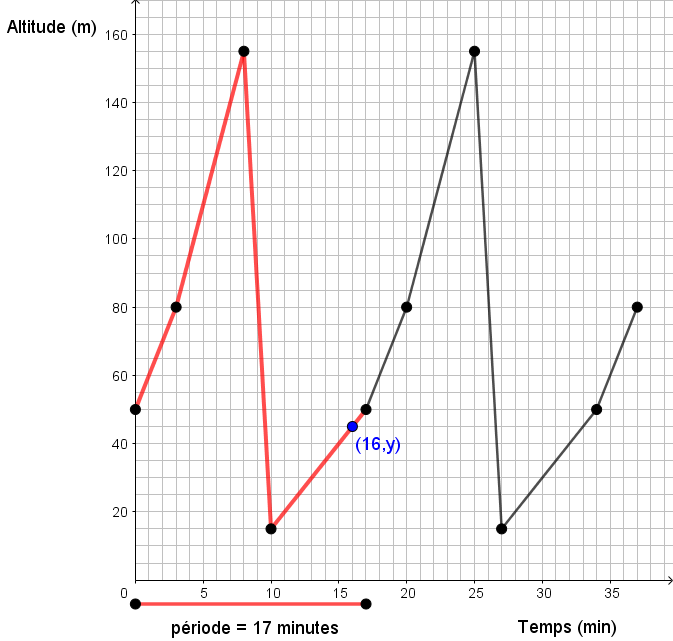
Lors d'une course en vélo de montagne, les participants doivent effectuer la même boucle à plusieurs reprises. Voici un graphique qui illustre la hauteur en altitude (en mètres) par rapport au temps écoulé depuis le départ d'un des compétiteurs.
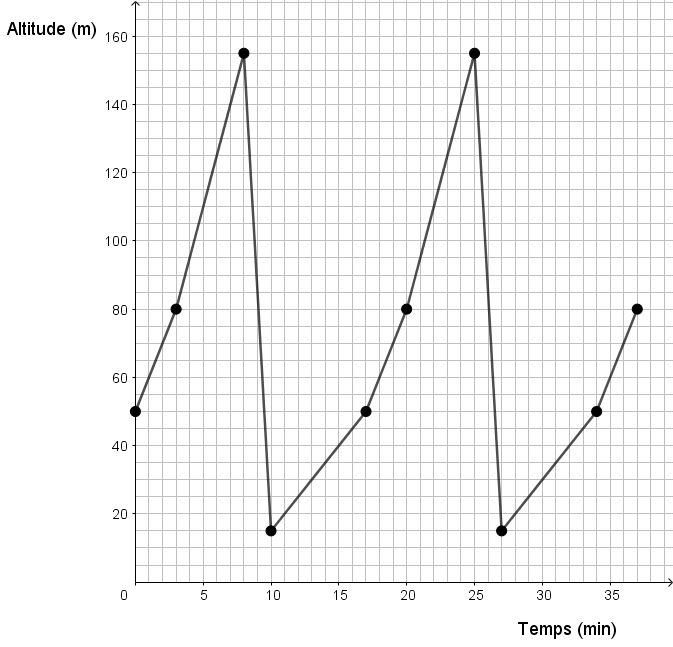
À l'aide de ces données, détermine l'altitude de ce cycliste à la 54e minute, puis à la 84e minute.
Solution pour la 54e minute :
1) Trouver le cycle et déterminer la période.
Pour y arriver, le tout passe par l'analyse du graphique. En d'autres mots, il s'agit de trouver la portion de celui-ci qui se répète.
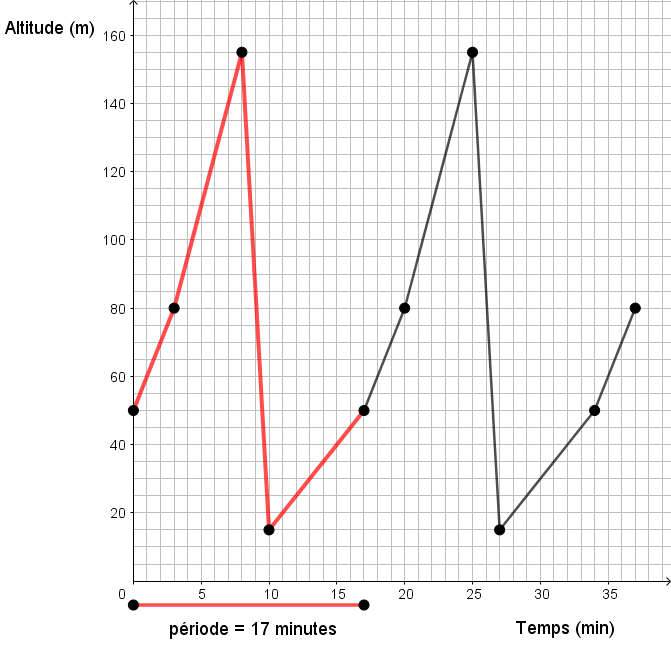
En analysant attentivement le graphique, on en déduit que le cycle commence à la coordonnée |(0,50)| et se termine à |(17,50)|. Ainsi, il y a un écart de 17 minutes entre ces deux coordonnées |(17 - 0 = 17)|.
2) Utiliser la période pour rapporter le point donné au cycle connu.
Par définition de la période, on peut rapporter le point situé à 54 minutes sur le cycle identifié à l'étape précédente. En soustrayant la période à plusieurs reprises, on obtient :
||\begin{align}
\text{Nombre de périodes complètes}\ & = \ \ 54 \div 17 \\
& \approx \ \ 3{,}18 \\
& \approx \ \ 3 \end{align}||
Ainsi, on en déduit que l'on doit « reculer » de 3 périodes, soit de |3 \times 17 = 51| minutes. Au final, |54 - 51 = 3| minutes.
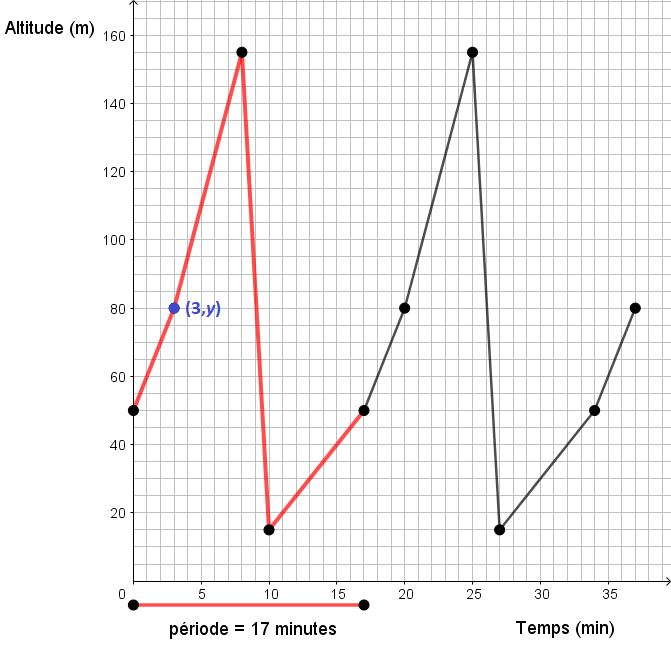
3) Trouver l'équation de la droite associée au point donné (si nécessaire).
Comme nous avons «atterri» directement sur un point remarquable du premier cycle, nous n'avons pas besoin de trouver l'équation de la droite.
4) Déterminer la coordonnée manquante.
Puisqu'on cherche la valeur en |x = 3|, l'observation du graphique nous donne directement la réponse : |y=80|. Finalement, on peut déduire qu'à la 54e minute, le cycliste se trouve à une altitude de |80| mètres.
Solution pour la 84e minute :
1) Trouver le cycle et déterminer la période.
Puisque c'est la même mise en situation, la période est toujours de 17 minutes.
2) Utiliser la période pour rapporter le point donné au cycle connu.
Par définition de la période, on peut rapporter le point situé à 84 minutes sur le cycle identifié à l'étape précédente. En soustrayant la période à plusieurs reprises, on obtient :
||\begin{align}
\text{Nombre de périodes complètes} & = \ \ 84 \div 17 \\
& \approx \ \ 4{,}94 \\
& \approx \ \ 4 \end{align}||
Ainsi, on en déduit que l'on doit « reculer » de 4 périodes, soit de |4 \times 17 = 68| minutes. Au final, |84 - 68 = 16| minutes.
3) Trouver l'équation de la droite associée au point donné.
Puisque cette section est représentée par une droite, on peut trouver son équation sous la forme |y=ax+b| en utilisant les points remarquables |(10,15)| et |(17,50)|.
||\begin{align} a & =\ \frac{y_2-y_1}{x_2-x_1} \\ & =\ \frac{50 - 15}{17 - 10} \\ & =\ 5 \\ \\ \Rightarrow\ \ y & = 5x + b \\ 15 & = 5 (10) + b \\ 15 & = 50 + b \\ -35 & = b \\ \\ \Rightarrow\ \ y & = 5x - 35 \end{align}||
4) Déterminer la coordonnée manquante.
Puisqu'on cherche la valeur en |x = 16|, on peut utiliser l'équation de la droite trouvée à l'étape précédente pour déterminer la valeur en |y:| ||\begin{align} y\ \ & =\ \ 5x - 35 \\ \Rightarrow \ \ y\ \ & =\ \ 5 (16) - 35 \\ & =\ \ 80 - 35 \\ & =\ \ 45 \end{align}||Finalement, on peut déduire qu'à la 84e minute, le cycliste se trouve à une altitude de |45| mètres.
Pour valider ta compréhension à propos de la résolution graphique de fonctions périodiques, en escalier et définies par parties de façon interactive, consulte la MiniRécup suivante.

<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p><span>Certaines fonctions périodiques sont très connues et leur étude est indispensable. Non seulement ces fonctions permettent de modéliser des phénomènes physiques tels que les ondes, mais elles permettent également de faire un lien avec la géométrie. Il s'agit des <a href="/fr/eleves/bv/mathematiques/les-fonctions-trigonometriques-m1459">fonctions trigonométriques</a>. </span></p>
</body></html>