Graphically, periodic functions are functions with a pattern that repeats itself over and over in the Cartesian plane.
To fully understand what ‘periodic’ means, it is important to fully grasp the concepts of a cycle and a period.
The shortest interval of a graph which corresponds to just one unit of a repeating pattern is called the cycle of a function.
The distance between the two |x|-coordinates located at the ends of the same cycle is called the period.
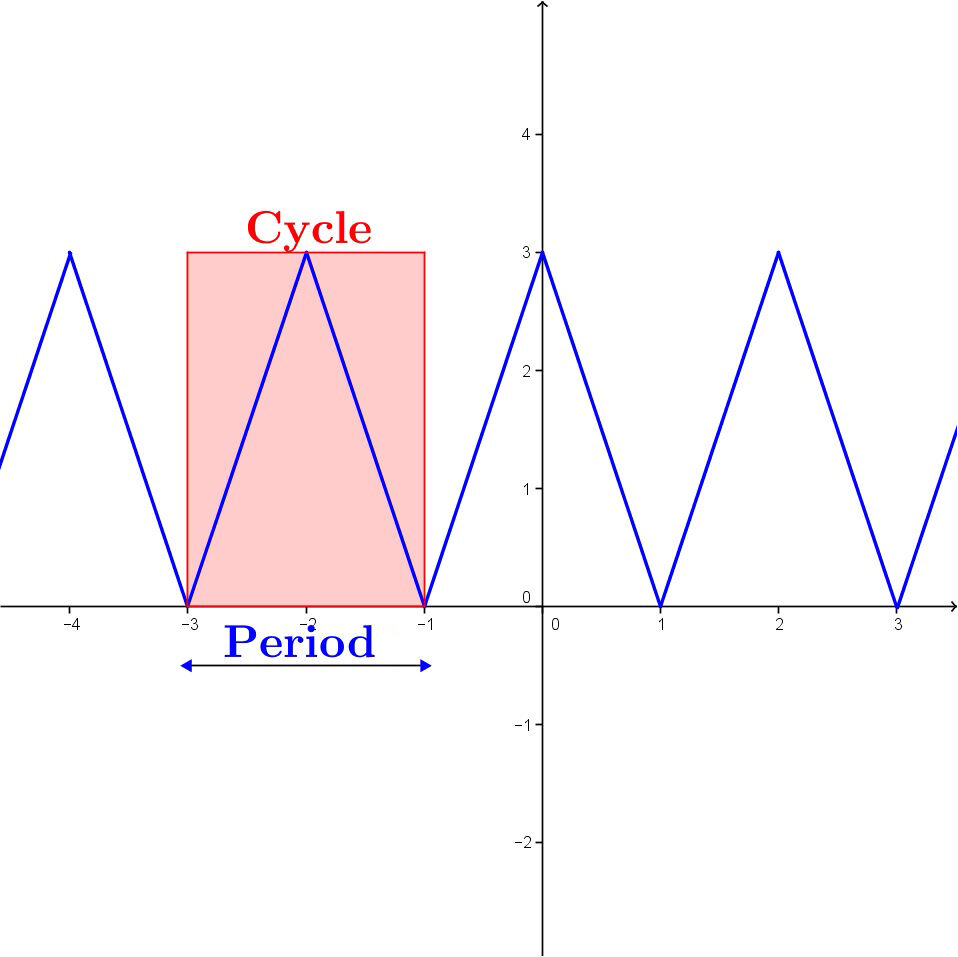
To illustrate these concepts, the following animation shows a period and its value.
To solve this kind of problem, it is absolutely necessary to start by finding the cycle and the period of the periodic function.
-
Find the cycle and the period.
-
Use the period to relate the given point to the cycle.
-
Find the linear equation associated with the given point (if necessary).
-
Find the missing point.
The following situation could occur in real life.
During a mountain bike race, participants must complete the same lap several times. Here is a graph showing the altitude (in metres) of the ground relative to the time that has passed since the start of the race for one of the competitors.

Using the data above, determine the altitude of the rider at the |54th| and |84th| minute.
Solution to the |54th| minute
-
Find the cycle and the period
To solve this problem, analyze the graph. In other words, find the cycle that repeats itself.
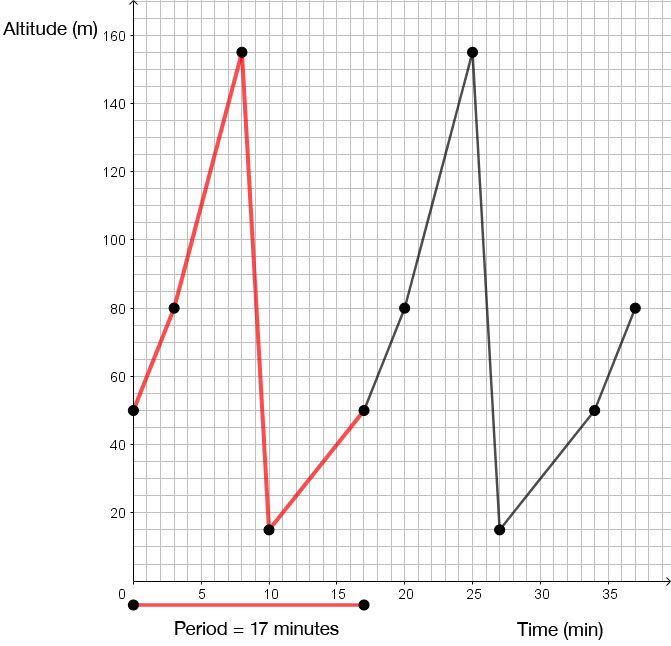
By carefully analyzing the graph, notice that the cycle begins at the point |(0,50)| and ends at |(17,50)|. So, there is a difference of |17| minutes between these two points |(17 - 0 = 17)|.
-
Use the period to relate the given point to the cycle
Using the definition of the period, we can relate the point located at |54| minutes with the cycle identified in the previous step. By subtracting the period several times, we find that:
||\begin{align}
\text{Number of completed periods}\ & = \ \ 54 \div 17 \\
& \approx \ \ 3.18 \\
& \approx \ \ 3 \end{align}||
Therefore, we must “backtrack” by |3| periods, that is, by |3 \times 17 = 51| minutes. Then, calculate |54 - 51 = 3| minutes.

-
Find the linear equation associated with the given point (if necessary)
Since we have "landed" directly on a clear point of the first cycle, it is not necessary to find the equation of the associated line.
-
Find the missing point
Looking for the value at |x = 3|, the graph directly gives the answer: |y=80.| Thus, at the |54th| minute, the cyclist is at an altitude of |80| metre.
Solution to the |84th| minute
-
Find the cycle and determine the period
Since the problem is the same, the period is still |17| minutes.
-
Use the period to relate the given point to the known cycle
Using the definition of the period, we can relate the point located at |84| minutes to the cycle identified in the previous step. By subtracting the period several times, the result is the following:
||\begin{align}
\text{Number of completed periods} & = \ \ 84 \div 17 \\
& \approx \ \ 4.94 \\
& \approx \ \ 4 \end{align}||
Therefore, we must “backtrack” by |4| periods, that is, by |4 \times 17 = 68| minutes. Then, subtract |84 - 68 = 16| minutes.
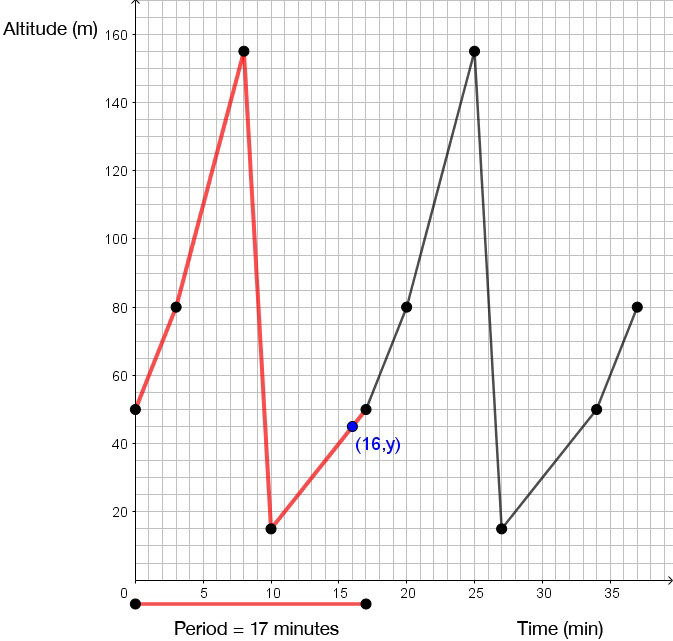
-
Find the linear equation associated with the given point
Since the point is located on a straight line, its equation has the form |y=ax+b|. Use the nearby points |(10,15)| and |(17,50)| to find the equation of the line.
||\begin{align} a & =\ \dfrac{y_2-y_1}{x_2-x_1} \\ & =\ \dfrac{50 - 15}{17 - 10} \\ & =\ 5 \\ \\ \Rightarrow\ \ y & = 5x + b \\ 15 & = 5 (10) + b \\ 15 & = 50 + b \\ -35 & = b \\ \\ \Rightarrow\ \ y & = 5x - 35 \end{align}||
-
Find the missing point
Since we desire the value at |x = 16|, use the linear equation found in the previous step to determine the value of |y:| ||\begin{align} y\ \ & =\ \ 5x - 35 \\ \Rightarrow \ \ y\ \ & =\ \ 5 (16) - 35 \\ & =\ \ 80 - 35 \\ & =\ \ 45 \end{align}|| Thus, at the |84th| minute, the cyclist was at an altitude of |45| metres.
Pour valider ta compréhension à propos de la résolution graphique de fonctions périodiques, en escalier et définies par parties de façon interactive, consulte la MiniRécup suivante.

Certain periodic functions are very well-known. Studying them is essential. Not only do these functions allow the modeling of physical phenomena such as waves, but they also have connections to geometry. These are the trigonometric functions.