Les fractions équivalentes sont des fractions qui représentent le même nombre, la même proportion.
-
Afin d'exprimer une fraction équivalente à une autre, on doit utiliser la multiplication ou la division.
-
Il est important de se souvenir que toute multiplication ou division doit être faite à la fois au numérateur et au dénominateur.
Si on multiplie le numérateur par 2, on doit aussi multiplier le dénominateur par 2.
Pour passer d'une fraction à une autre fraction équivalente, on peut multiplier ou diviser cette fraction par une fraction-unité |\left(\dfrac { 2 }{ 2 } ,\dfrac { 3 }{ 3 } ,\dfrac { 6 }{ 6 }\right)|
On cherche des fractions équivalentes à |\dfrac { 3 }{ 4 }.|
A) On peut décider de multiplier par la fraction-unité : |\dfrac { 2 }{ 2 }|
|\dfrac { 3 }{ 4 } \times \dfrac { 2 }{ 2 } =\dfrac { 3\times 2 }{ 4\times 2 } =\dfrac { 6 }{ 8 }| (fraction équivalente)
B) On peut aussi décider de multiplier par |\dfrac { 5 }{ 5 }|
|\dfrac { 3 }{ 4 } \times \dfrac { 5 }{ 5 } =\dfrac { 3\times 5 }{ 4\times 5 } =\dfrac { 15 }{ 20 }| (fraction équivalente)
On peut utiliser un rectangle pour représenter une fraction. On peut comparer ce rectangle à une tablette de chocolat à partager.
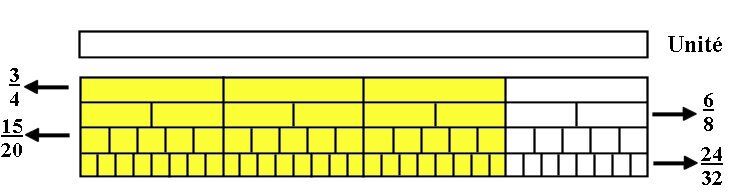
On remarque que peu importe le nombre de divisions, la surface de toutes les portions reste la même. Les parties colorées en jaune représentent la fraction utilisée (le numérateur de la fraction). On se rend vite compte que l’on pourrait encore diviser le rectangle en de plus petites parties et trouver d’autres fractions équivalentes.
On peut utiliser un cercle pour représenter une fraction. On peut comparer ce cercle à une tarte ou une pizza à partager.
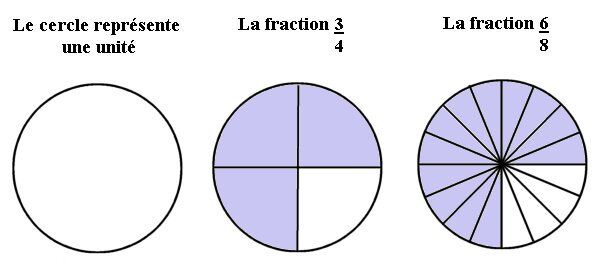
Que l'on mange 3 morceaux de tarte sur 4 (la deuxième tarte), 6 morceaux sur 8 ou 12 morceaux sur 16 (la troisième tarte), on aura mangé la même quantité de tarte. Ces trois fractions sont donc équivalentes. On pourrait encore diviser la tarte. Plus on divise la tarte, plus les portions sont petites, mais on mange toujours la même quantité de tarte.
L’avantage de disposer les fractions sur une droite numérique est que l’on peut représenter les fractions négatives aussi, ce qui est impossible avec des dessins comme les cercles et les rectangles.
On doit positionner les droites numériques les unes au-dessus des autres afin de bien voir les fractions équivalentes. Toutes les fractions superposées sont équivalentes.
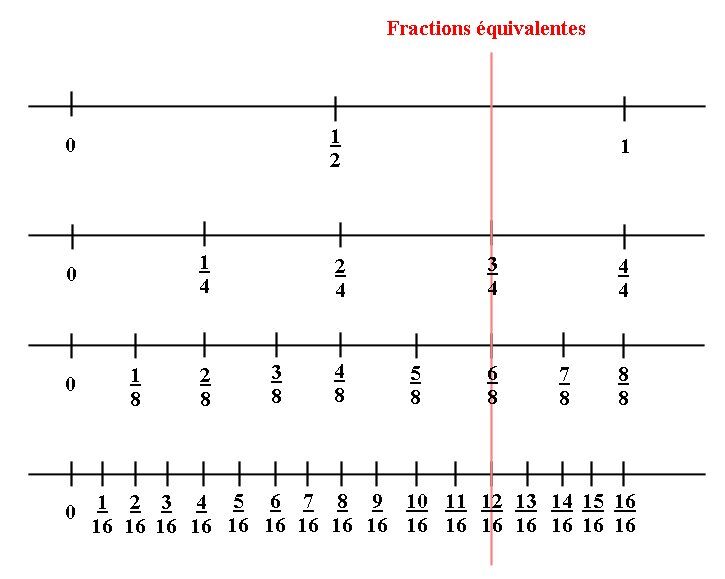
La méthode la plus facile pour réduire une fraction est la division. Il s'agit de trouver un diviseur commun au numérateur et au dénominateur.
On cherche à réduire la fraction |\dfrac { 24 }{ 32 }| pour trouver une fraction équivalente.
Puisque le numérateur et le dénominateur sont des nombres pairs, on peut les diviser par |2.| ||\dfrac { 24\div 2 }{ 32\div 2 } =\dfrac { 12 }{ 16 }||
Donc |\dfrac { 12 }{ 16 }| est une fraction équivalente à |\dfrac { 24 }{ 32 }.|
On peut aussi diviser le numérateur et le dénominateur par |4.| ||\dfrac { 24\div 4 }{ 32\div 4 } =\dfrac { 6 }{ 8 }||
Lorsqu’aucune division n'est possible, c'est que la fraction est irréductible ou sous sa forme la plus réduite.
On divise le numérateur et le dénominateur par le même nombre, et on répète ainsi successivement jusqu’à ce qu’on ne soit plus capable de trouver de diviseur commun aux deux termes. ||\dfrac { 24\div 2 }{ 32\div 2 } =\dfrac { 12 }{ 16 }\;\;\;\dfrac { 12\div 2 }{ 16\div 2 } =\dfrac { 6 }{ 8 }\;\;\;\dfrac { 6\div 2 }{ 8\div 2 } =\dfrac { 3 }{ 4 }||
Comme |3| et |4| n'ont pas de diviseur commun autre que |1,| la fraction est irréductible.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Étape 1 : On calcule le <a href="/fr/eleves/bv/mathematiques/plus-grand-commun-diviseur-pgcd-m1064">PGCD</a> des deux termes.</p>
<p>Étape 2 : On divise les deux termes par le PGCD.</p>
</body></html>
Réduction de la fraction |\dfrac { 24 }{ 32 }|
Étape 1 : PGCD |(24,32) = 8|
Étape 2 : |\dfrac { 24\div 8 }{ 32\div 8 } =\dfrac { 3 }{ 4 }|
Pour valider ta compréhension des fractions de façon interactive, consulte la MiniRécup suivante :
