La notation fractionnaire est une façon d'écrire les nombres rationnels. Cette notation comprend deux formes d'écritures : les fractions et les nombres fractionnaires.
Une fraction est un nombre rationnel exprimé par une division non effectuée entre deux nombres entiers |a| et |b| où | b\neq 0|. En d'autres mots,
||\left\{ \frac{a}{b} \in \mathbb{Q} \mid a,b \in \mathbb{Z} \ \text{et} \ b \neq 0\right\}||
On représente généralement les fractions comme ceci : ||a/b\qquad \text{ou}\qquad \frac{a}{b}||
Dans cette représentation,
-
|a| représente le numérateur, le nombre du haut.
-
|b| représente le dénominateur, le nombre du bas.
-
Le trait ou la barre de fraction signifie que le numérateur est divisé par le dénominateur.
Le dénominateur doit toujours être différent de |0,| car la division par |0| est indéfinie en mathématique. Le numérateur, pour sa part, peut prendre n'importe quelle valeur entière, positive ou négative.
Dans la fraction suivante, le numérateur est |3| et le dénominateur |5.|

Un nombre fractionnaire est un nombre rationnel qui contient une partie entière, composée d'une ou de plusieurs unités, et une partie fractionnaire qui est composée d'une fraction.
Les nombres fractionnaires sont une façon d'écrire les fractions impropres.
Dans le nombre fractionnaire suivant, la partie entière est |6| et la partie fractionnaire est |\dfrac{1}{4}.|
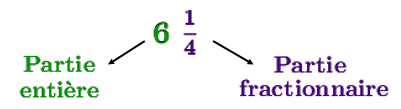
Ce nombre se lit « |6| et un quart ». Il est une représentation de la fraction impropre |\dfrac{25}{4}|.
Pour bien comprendre la notation fractionnaire et pouvoir l'utiliser en contexte, il importe de connaitre les différents sens de la fraction.
La fraction peut être vue comme une partie d'un tout.
Dans ce mode de représentation, le dénominateur correspond au nombre de parties égales qui divisent le tout.
Le numérateur, lui, correspond au nombre de parties égales utilisées.
En gardant en mémoire cette relation entre le numérateur et le dénominateur, on peut toujours construire une fraction à partir d'un tout.
Voici deux représentations d'une fraction comme étant la partie d'un tout.
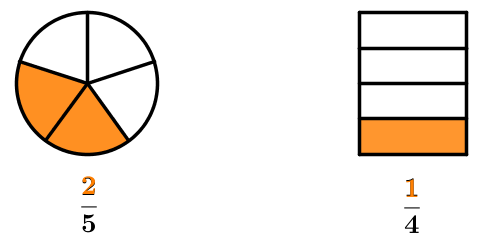
On remarque que, dans les deux exemples, le nombre de parties égales contenues dans la figure correspond aux dénominateurs des fractions, alors que le nombre de parties utilisées correspond aux numérateurs.
Par contre, il peut arriver qu'on utilise le même tout plus d'une fois. Par exemple, on peut avoir recours à plusieurs gâteaux identiques lors d'une même fête.
L'illustration ci-dessous représente la fraction |\dfrac{7}{3}.|
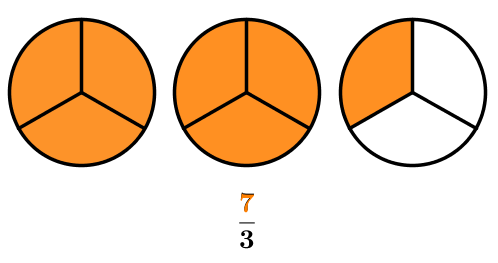
Comme le numérateur de la fraction est plus grand que le dénominateur, on doit utiliser plus d'une figure. Cependant, comme à l'exemple précédent, on remarque que le dénominateur correspond toujours au nombre de parties égales contenues dans un seul tout et que le numérateur correspond au nombre de parties utilisées au total.
Dans ce cas précis, on peut utiliser le nombre fractionnaire pour écrire cette fraction puisque le numérateur a une valeur plus grande que le dénominateur.
En se fiant à l'illustration, on remarque que le nombre |\dfrac{7}{3}| comprend deux entiers et le tiers d'un troisième. La représentation en nombre fractionnaire de cette fraction impropre est donc :
||\frac{7}{3}=2 \frac{1}{3}||
La fraction peut également représenter une comparaison entre deux grandeurs de même nature.
On s'interesse ici au rapport entre le nombre de billes vertes et le nombre de billes bleues contenues dans le sac de billes suivant.
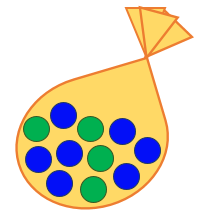
La fraction représentant ce rapport est : |\dfrac{\color{green}{4}}{\color{blue}{7}}|
Dans cette situation, cette fraction signifie que pour |4| billes vertes, on a |7| billes bleues.
Cet exemple évoque maintenant une relation « partie par partie » et non « partie d'un tout » comme le présentait la section précédente.
À voir aussi
Comme il a été mentionné dans la définition d'une fraction, celle-ci est exprimée comme une division non-effectuée entre deux nombres : le numérateur et le dénominateur.
Ainsi, la fraction peut être vue comme la simple division du numérateur par le dénominateur.
Le résultat de cette division correspond à la notation décimale du nombre rationnel représenté par la fraction.
Fraction
Prenons la fraction |\dfrac{3}{4}.| En considérant cette fraction comme une division, on obtient ||\dfrac{3}{4}=3\div 4=0{,}75|| On a donc que |0{,}75| est la représentation en notation décimale du nombre rationnel représenté par |\dfrac{3}{4}.|
Nombre fractionnaire
Prenons maintenant la fraction |\dfrac{12}{5}.| Toujours en considérant cette fraction comme une division, on obtient ||\dfrac{12}{5}=12\div 5=2{,}4|| On a donc que |2{,}4| est la représentation en notation décimale du nombre rationnel représenté par |\dfrac{12}{5}.|
En effectuant l'opération de la division, on obtient un nombre qui représente la même quantité, mais qui est écrit à l'aide d'une autre forme d'écriture.
En effet, on peut utiliser différentes formes d'écriture pour représenter une quantité. Par exemple :
||\begin{align} {\small\frac{11}{5}} &= 2{\small\frac{1}{5}} && \text{fraction et nombre fractionnaire} \\
&= 2{,}2 && \text{nombre à notation décimale} \\
&= 220\ \% && \text{pourcentage} \end{align}||
Pour valider ta compréhension des fractions de façon interactive, consulte la MiniRécup suivante :
