Equivalent fractions are fractions representing the same quantity or same proportion.
-
Multiplication or division is used to obtain a fraction that is equivalent to another.
-
It is important to remember to multiply or divide both the numerator and the denominator.
If we multiply the numerator by 2, we must also multiply the denominator by 2.
To find a fraction that is equivalent to another, multiply or divide the fraction by a fraction whose numerator and denominator are the same |\left(\dfrac { 2 }{ 2 },\dfrac { 3 }{ 3 },\dfrac { 6 }{ 6 }\right)|
Find equivalent fractions to |\dfrac { 3 }{ 4 }.|
A) We can multiply by: |\dfrac { 2 }{ 2 }|
|\dfrac { 3 }{ 4 } \times \dfrac { 2 }{ 2 } =\dfrac { 3\times 2 }{ 4\times 2 } =\dfrac { 6 }{ 8 }| (equivalent fraction)
B) We can also multiply by |\dfrac { 5 }{ 5 }|
|\dfrac { 3 }{ 4 } \times \dfrac { 5 }{ 5 } =\dfrac { 3\times 5 }{ 4\times 5 } =\dfrac { 15 }{ 20 }| (equivalent fraction)
Fraction strips can be used to represent equivalent fractions. The whole rectangle can be compared to sharing a chocolate bar.
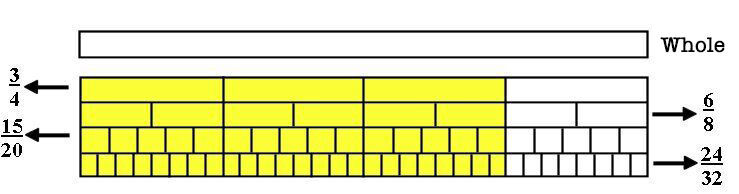
Regardless of the number of divisions, the area of each full strip remains the same. The parts coloured in yellow represent the fraction’s numerator. The rectangle can be divided into smaller strips and other equivalent fractions can be found.
A circle can be used to represent a fraction. The circle can be compared to sharing a pie or a pizza.
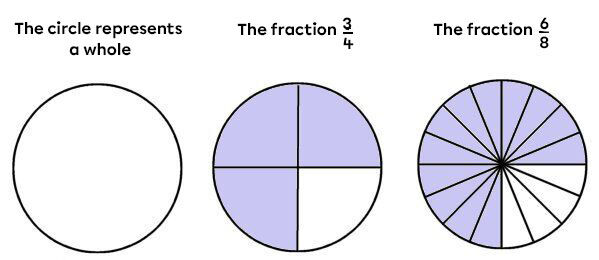
Whether 3 out of 4 pieces of pie are eaten, 6 out of 8 pieces, or 12 out of 16 pieces, the same amount of pie will have been eaten. Therefore, the three fractions are equivalent. The pie could be divided even further. The more the pie is divided, the smaller the portions become. However, the same amount of pie is always eaten.
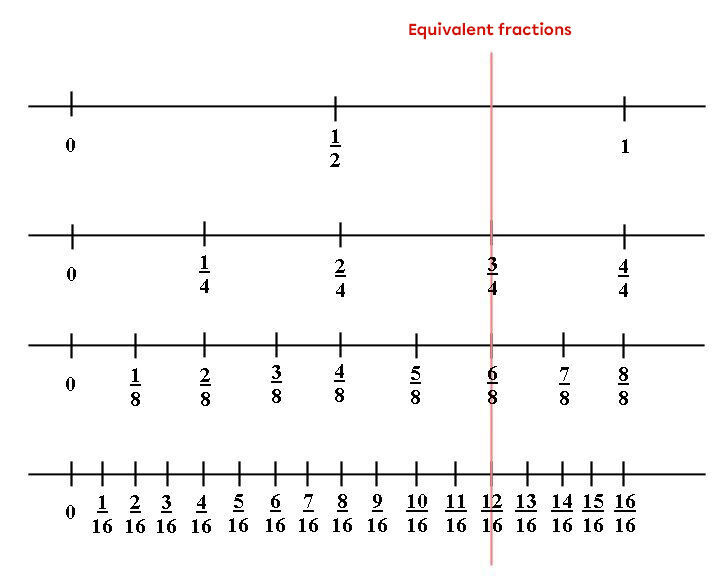
The advantage of arranging fractions on a number line is that negative fractions can be represented as well, which is not possible with drawings like circles and rectangles.
The number lines must be placed one above the other to clearly see the equivalent fractions. The fractions that line up are all equivalent.
The easiest way to simplify a fraction is to use division. The first step is to find a common divisor for both the numerator and the denominator.
Simplify the fraction |\dfrac { 24 }{ 32 }| to find an equivalent fraction.
Since the numerator and denominator are even numbers, they can be divided by |2.| ||\dfrac { 24\div 2 }{ 32\div 2 } =\dfrac { 12 }{ 16 }||
So, |\dfrac { 12 }{ 16 }| is an equivalent fraction to |\dfrac { 24 }{ 32 }.|
The numerator and the denominator can also be divided by |4.| ||\dfrac { 24\div 4 }{ 32\div 4 } =\dfrac { 6 }{ 8 }||
When a division is not possible, the fraction is irreducible or in its simplified form.
The numerator and the denominator are divided by the same number. The division is repeated over and over until it is no longer possible to find a common divisor for the two terms. ||\dfrac { 24\div 2 }{ 32\div 2 } =\dfrac { 12 }{ 16 }\;\;\;\dfrac { 12\div 2 }{ 16\div 2 } =\dfrac { 6 }{ 8 }\;\;\;\dfrac { 6\div 2 }{ 8\div 2 } =\dfrac { 3 }{ 4 }||
Since |3| and |4| have no common factor other than |1,| the fraction is simplified.
Step 1: Find the GCF of the two terms.
Step 2: Divide the two terms by the GCF.
Simplify the fraction |\dfrac { 24 }{ 32 }|
Step 1: GCF |(24,32) = 8|
Step 2: |\dfrac { 24\div 8 }{ 32\div 8 } =\dfrac { 3 }{ 4 }|
To confirm that you understand fractions, see the following interactive CrashLesson:
