<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p><strong>L’<a href="/fr/eleves/bv/mathematiques/l-homothetie-m1270">homothétie</a> </strong>est une transformation qui permet d’agrandir ou de réduire une figure. On réalise l'homothétie à partir d’un centre d’homothétie (O) et d’un rapport d'homothétie (k). On note l'homothétie |h_{(O,k)}|.</p>
</body></html>
Lorsque le centre d’homothétie se trouve au point origine dans un plan cartésien, l’homothétie est représentée par une règle de transformation de la forme :
|h_{(O,k)}:(x,y) \mapsto (kx,ky)|.
|h| indique que c'est une homothétie, |O| indique que le centre d'homothétie est à l'origine et |k| est le rapport d’homothétie.
Cette règle signifie qu’une homothétie de centre |O| et de rapport |k| pratiquée sur un point de coordonnées |(x, y)| donnera le point image |(kx , ky)|. Il s’agit donc de multiplier les coordonnées |x| et |y| par le rapport d’homothétie.
Le centre d'homothétie peut se trouver soit à l'intérieur ou à l'extérieur de la figure, mais c’est toujours la même règle qui s’applique. Les rapports d’homothétie peuvent être positifs ou négatifs, entiers ou fractionnaires.
Voici l'impact du rapport d'homothétie sur une figure selon sa valeur :
|
|k > 1| |
Agrandissement (dilation) de la figure initiale |
|
|0 < k < 1| |
Réduction (contraction) de la figure initiale |
|
|k = 1|
|
Aucun changement
|
| |k < -1| |
Agrandissement (dilation) de la figure initiale et la figure image change d’orientation. |
|
|-1 < k < 0| |
Réduction (contraction) de la figure initiale et la figure image change d'orientation. |
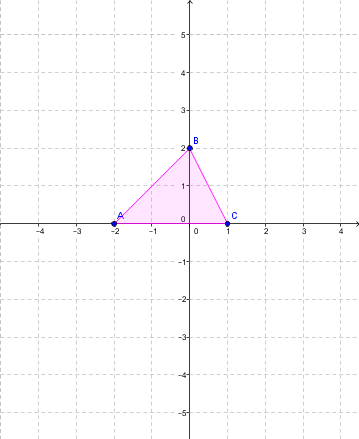
Exemple pour |k > 1|
Effectue l'homothétie suivante dont le |k = 2| et dont le centre se trouve à l'origine.
Étape 1 : Identifier les sommets du triangle rose (figure initiale).
|A (-2 , 0)|
|B (0 , 2)|
|C (1 , 0)|
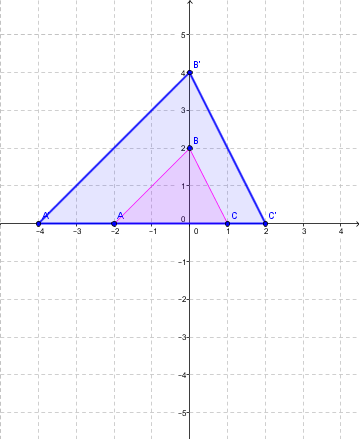
Étape 2 : Avec la règle, on trouve les coordonnées des points de la figure image à l'aide de la règle suviante:
|h_{(O,2)}:(x,y) \mapsto (2x,2y)|.
Les sommets deviennent donc:
|A (-2 , 0) \mapsto(-4 , 0) = A’|;
|B (0 , 2) \mapsto (0 , 4) = B’|;
|C (1 , 0) \mapsto (2 , 0) = C’|.
Étape 3 : On peut maintenant tracer le triangle bleu (figure image) résultant de l'homothétie. On remarque que les côtés du triangle ont subi une dilatation.
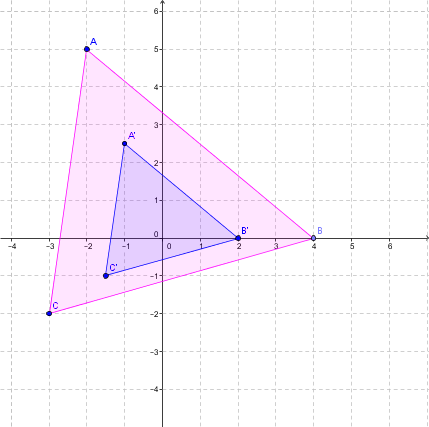
Exemple pour |0<k<1|
Effectue l'homothétie suivante dont le |k =1/2| et dont le centre se trouve à l'origine.
Étape 1 : Identifier les sommets du triangle rose (figure initiale).
|A (-2 , 5)|
|B (4 , 0)|
|C (-3 , -2)|

Étape 2 : Avec la règle, on trouve les coordonnées des points de la figure image à l'aide de la règle suivante:
|h_{(O,1/2)}:(x,y) \mapsto (\frac{1}{2} x, \frac{1}{2} y)|.
Les sommets deviennent donc:
|A (-2 , 5) \mapsto ( -1 , 2,5) = A’|;
|B (4 , 0) \mapsto (2 , 0) = B’|;
|C (-3 , -2) \mapsto (-1,5 , -1) = C’|.
Étape 3 : On peut maintenant tracer le triangle bleu (figure image) résultant de l'homothétie. On remarque que les côtés du triangle ont subi une contraction.
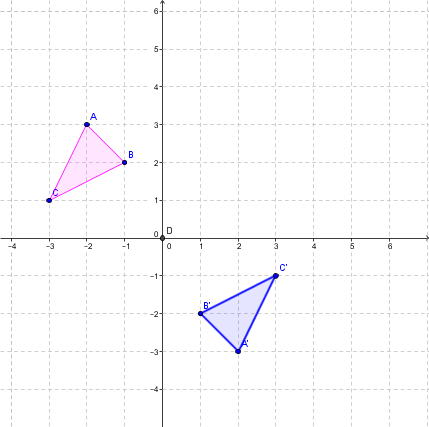
Exemple pour |k = -1|
Effectue l'homothétie suivante dont le |k = -1| et dont le centre se trouve à l'origine.
Étape 1 : Identifier les sommets du triangle rose (figure initiale).
|A (-2 , 3)|
|B (-1 , 2)|
|C (-3 , 1)|
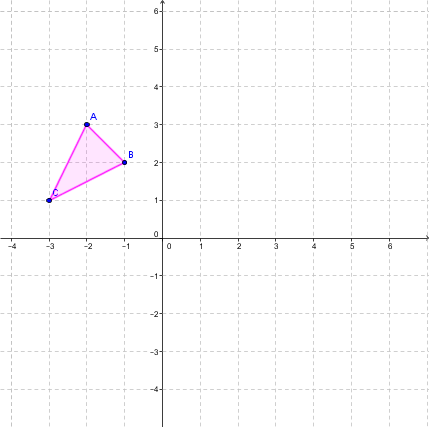
Étape 2 : Avec la règle, on trouve les coordonnées des points de la figure image à l'aide de la règle suivante:
|h_{(O,-1)}:(x,y) \mapsto (-1x, -1y)|.
Les sommets deviennent donc:
|A (-2 , 3) \mapsto ( 2 , -3) = A’|;
|B (-1 , 2) \mapsto (1 , -2) = B’|;
|C (-3 , 1) \mapsto (3 , -1) = C’|.
Étape 3 : On peut maintenant tracer le triangle bleu (figure image) résultat de l'homothétie. On remarque que le triangle a subi un changement d'orientation.