Les transformations géométriques permettent d'associer à toute figure initiale, une figure image (figure finale).
Il y a quatre principales transformations géométriques:
- la translation;
- la rotation;
- la réflexion;
- l'homothétie.
Une transformation géométrique qui ne modifie pas les mesures d'une figure est une isométrie. La translation, la rotation et la réflexion sont toutes des isométries.
Une transformation géométrique qui associe des figures dites semblables est appelée une similitude. L'homothétie est une similitude.
Lorsque l'on effectue plusieurs transformations géométriques successivement, la règle qui relie ces transformations est une composition et le résultat est appelé la composée. On utilise le symbole |\circ| qui se dit «rond».
La composition |t_{(a,b)} \circ s_x| correspond à la réflexion d'une figure par rapport à l'axe des |x| suivie d'une translation. On lit la composition «|t| rond |s_x|».
Remarques:
- On effectue les transformations de la droite vers la gauche.
- Une réflexion suivie d'une translation (dans la même direction que l'axe de réflexion) est une isométrie appelée symétrie glissée.
Pour savoir comment effectuer les différentes transformations géométriques dans un plan cartésien, vous pouvez consulter les fiches suivantes:
Pour reconnaitre les transformations, il suffit de bien maitriser les règles et de les associer aux bonnes transformations.
| Règles | Transformations | Remarques |
| |(x,y) \mapsto (x+a,y+b)| | Translation de |a| unités horizontalement et de |b| unités verticalement | C’est la seule transformation qui implique des |+| et des |-|. |
| |(x , y) \mapsto (-y, x)| | Rotation de |90°| ou |-270°| centrée à l'origine | On a changé l’ordre des lettres et la première coordonnée devient négative. |
| |(x , y) \mapsto (-x, -y)| | Rotation de |180°| ou de |-180°| centrée à l'origine |
Puisque la figure fait un demi-tour, on ne fait que changer les signes. |
| |(x , y) \mapsto (y, -x)| | Rotation de |270°| ou de |-90°| centrée à l'origine | On a changé l’ordre des lettres et la deuxième coordonnée devient négative. |
|
|(x,y) \mapsto (x,-y)| |
Symétrie par rapport à l’axe des |x| | Seul le |y| change de signe. |
| |(x , y) \mapsto (-x, y)| | Symétrie par rapport à l’axe des |y| | Seul le |x| change de signe. |
| |(x , y) \mapsto ( y, x)| | Symétrie par rapport à la bissectrice des quadrants |1| et |3| | On change l’ordre des lettres. |
| |(x , y) \mapsto (-y, -x)| | Symétrie par rapport à la bissectrice des quadrants |2| et |4| | On change tout, l’ordre et les signes. |
| |(x, y) \mapsto (kx, ky)| | Homothétie de rapport |k| | C’est la seule transformation qui implique des coefficients de multiplication différents de |1|. |
Pour trouver la transformation qui lie 2 figures dans un plan cartésien, il faut comparer les coordonnées des sommets homologues, c'est-à-dire le |A| avec le |A’|, le |B| avec le |B’|, et ainsi de suite.
Exemple de translation
On translate le triangle rose et on obtient alors le triangle bleu.
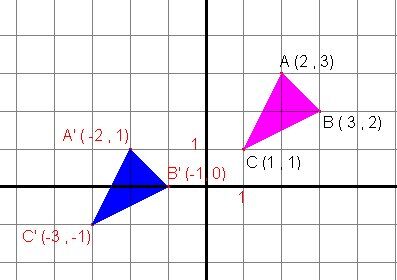
On compare les coordonnées des sommets homologues :
|A| et |A’|: |(2 , 3)| et |(-2 , 1)|;
|B| et |B’|: |(3 , 2)| et |(-1 , 0)|;
|C| et |C’|: |(1 , 1)| et |( -3 , -1)|.
On ne remarque pas de multiplication des coordonnées, pas de changement d’ordre et pas de changement de signe significatif. Il ne reste que la translation comme transformation admissible.
On trouve la règle :
La valeur en |x| du point |A| est passée de |2| à |-2|, c'est-à-dire une différence de |4|.
La valeur en |x| du point |B| est passée de |3| à |-1|, c'est-à-dire une différence de |4|.
La valeur en |x| du point |C| est passée de |1| à |-3|, c'est-à-dire une différence de |4|.
La valeur en |y| du point |A| est passée de |3| à |1|, c'est-à-dire une différence de |2|.
La valeur en |y| du point |B| est passée de |2| à |0|, c'est-à-dire une différence de |2|.
La valeur en |y| du point |C| est passée de |1| à |-1|, c'est-à-dire une différence de |2|.
La règle de la translation est donc : |t_{(-4,-2)} : (x , y) \mapsto (x – 4 , y – 2)|.