Dilation is a transformation that makes it possible to enlarge or reduce a figure. The dilation is made from a dilation centre (O) and a scale factor (k). Dilation is represented by |h_{(O,k)}|.
When the dilation’s centre is at the point of origin on a Cartesian plane, it is represented by this form of a transformation rule:
|h_{(O,k)}:(x,y) \mapsto (kx,ky)|.
|h| indicates that it is a dilation, |O| indicates that the centre of dilation is at the origin, and |k| is the scale factor.
This rule means that a dilation with centre |O| and scale factor |k| performed on a coordinate point |(x, y)|, will give the point image |(kx , ky)|. All that is required is to multiply the coordinates |x| and |y| by the scale factor.
The dilation’s centre can be either inside or outside the figure, but the same rule always applies. Scale factors can be positive or negative, whole or fractional.
Here is the impact of the scale factor on a figure according to its value:
|
|k > 1| |
Enlargement (expansion) of the initial figure |
|
|0 < k < 1| |
Reduction (shrinking) of the initial figure |
|
|k = 1|
|
No change
|
| |k < -1| |
Enlargement (expansion) of the initial figure and the image figure changes orientation |
|
|-1 < k < 0| |
Reduction (shrinking) of the initial figure and the image figure changes orientation |
Example for |k > 1|
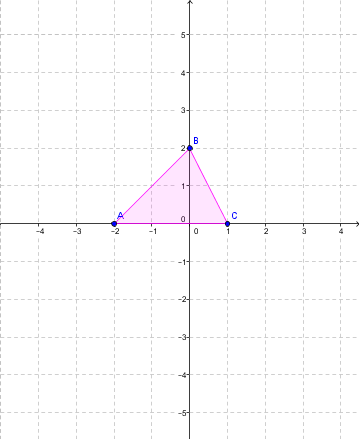
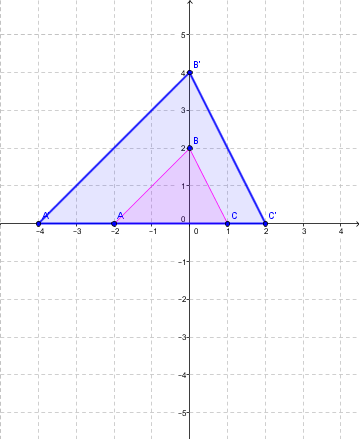
Complete the following dilation whose |k = 2| and whose centre is at the origin.
-
Identify the vertices of the pink triangle (initial figure).
|A (-2 , 0)|
|B (0 , 2)|
|C (1 , 0)|
-
Find the coordinates of the image figure’s points using the following rule: |h_{(O,2)}:(x,y) \mapsto (2x,2y)|.
The vertices then become:
|A (-2 , 0) \mapsto(-4 , 0) = A’|;
|B (0 , 2) \mapsto (0 , 4) = B’|;
|C (1 , 0) \mapsto (2 , 0) = C’|. -
Next, draw the blue triangle (figure image) resulting from the dilation. Notice how the sides of the triangle have enlarged.
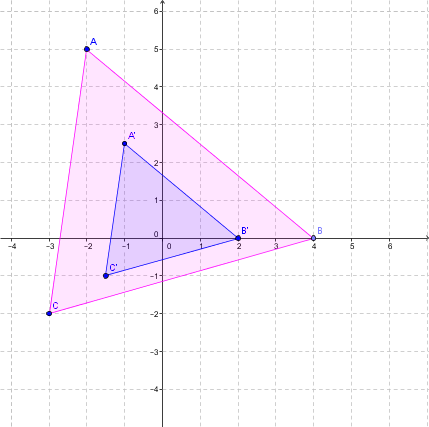
Example for |0<k<1|
Perform the following dilation whose |k =1/2| and whose centre is at the origin.
-
Step 1: Identify the vertices of the pink triangle (initial figure).
|A (-2 , 5)|
|B (4 , 0)|
|C (-3 , -2)|

-
Find the coordinates of the image figure’s points using the following rule:
|h_{(O,1/2)}:(x,y) \mapsto (\frac{1}{2} x, \frac{1}{2} y)|.
The vertices then become:
|A (-2 , 5) \mapsto ( -1 , 2,5) = A’|;
|B (4 , 0) \mapsto (2 , 0) = B’|;
|C (-3 , -2) \mapsto (-1,5 , -1) = C’|. -
Finally, draw the blue triangle (figure image) resulting from the dilation. Notice how the sides of the triangle have shrunk.
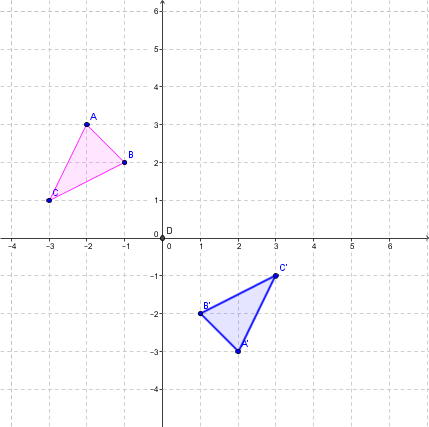
Example for |k = -1|
Perform the following dilation where |k = -1| and whose centre is at the origin.
-
Identify the vertices of the pink triangle (initial figure).
|A (-2 , 3)|
|B (-1 , 2)|
|C (-3 , 1)|
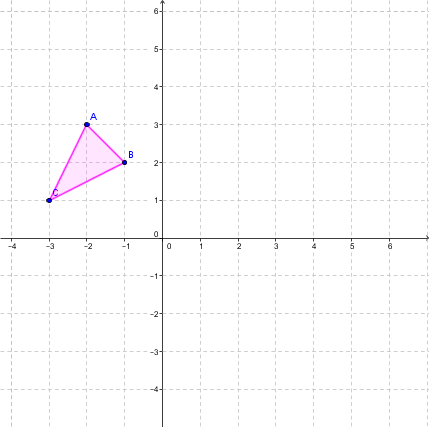
-
Find the coordinates of the image figure’s points using this rule: |h_{(O,-1)}:(x,y) \mapsto (-1x, -1y)|.
The vertices then become:
|A (-2 , 3) \mapsto (2 , -3) = A’|;
|B (-1 , 2) \mapsto (1 , -2) = B’|;
|C (-3 , 1) \mapsto (3 , -1) = C’|. -
Finally, draw the blue triangle (figure image) resulting from the dilation. Notice how the triangle has changed orientation.