Il existe une multitude de propriétés relatives aux diverses fonctions que l'on rencontre.
Le domaine d'une fonction |f| correspond à l'ensemble des valeurs que peut prendre sa variable indépendante, généralement |x|.
Le domaine d'une fonction peut être donné de différentes façons : ensembles de nombres, intervalles, accolades, etc.
Quel est le domaine de la fonction |f(x)=12x-1|? Cette fonction a pour graphique :
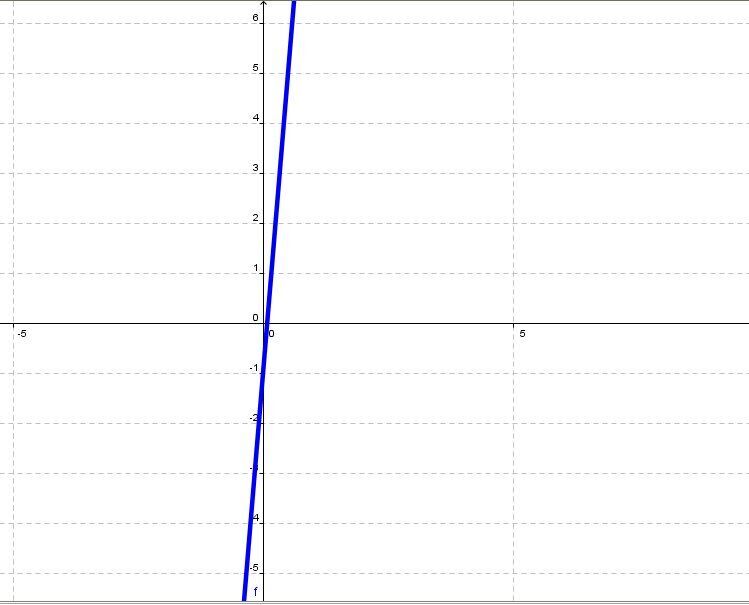
Le domaine de cette fonction est formé de tous les nombres réels, car les valeurs que la variable |x| peut prendre sont comprises entre l’infini négatif et l’infini positif.
En langage mathématique, on peut écrire le domaine des 3 façons suivantes :||\begin{align}\text{dom}(f)&=\mathbb{R}\\&\ \text{ou}\\\text{dom}(f)&=\; ]-\infty,+\infty[\\&\ \text{ou}\\\text{dom}(f)&=\{x\in\mathbb{R}\}\end{align}||
Au lieu d'écrire l'intervalle |]- \infty, + \infty[|, on écrit tout simplement |\mathbb{R}|.
L'image d'une fonction |f| correspond à l'ensemble des valeurs que peut prendre la variable dépendante, généralement |y|.
Par abus de langage, il est possible de confondre le concept d'image et de codomaine en prétendant que ce sont des synonymes. Or, ce n'est pas toujours le cas.
Concrètement, on définit l'image d'une fonction comme étant un sous-ensemble du codomaine de cette dernière. En d'autres mots, l'image n'est pas nécessairement équivalente au codomaine.
L'image d'une fonction peut être exprimée de différentes façons : ensembles de nombres, intervalles, accolades.
Quelle est l'image de la fonction |f(x) = 12x – 1|? Cette fonction a pour graphique :
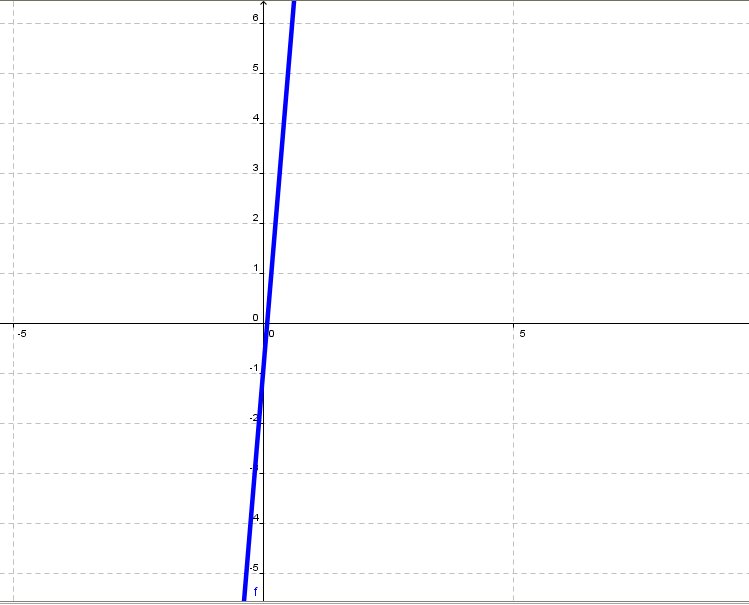
L'image de cette fonction est formée de tous les nombres réels, car les valeurs que la variable |y| peut prendre sont comprises entre moins l’infini et plus l’infini.
En langage mathématique, on peut écrire l'image des trois façons suivantes :||\begin{align}\text{ima}(f)&=\mathbb{R}\\&\ \text{ou}\\\text{ima}(f)&=\; ]-\infty,+\infty[\\&\ \text{ou}\\\text{ima}(f)&=\{f(x)\in\mathbb{R}\}\end{align}||
La variation d'une fonction est exprimée en termes de croissance, de décroissance et de constance.
On parle de croissance lorsque, sur un intervalle donné du domaine d'une fonction, l'image de celle-ci ne diminue pas. La croissance correspond donc à un intervalle en |x| sur lequel les valeurs de |y| ne diminuent pas : les valeurs de |y| augmentent ou restent constantes.
On parle de décroissance lorsque, sur un intervalle donné du domaine d'une fonction, l'image de celle-ci n'augmente pas. La décroissance correspond donc à un intervalle en |x| sur lequel les valeurs de |y| n'augmentent pas : elles diminuent ou restent constantes.
On dit qu’une fonction est constante (de variation nulle) si, pour un intervalle donné du domaine, les valeurs de l'image demeurent inchangées.
Une fonction est dite strictement croissante sur un intervalle de |x| si les valeurs de |y| ne font qu'augmenter.
Une fonction est dite strictement décroissante sur un intervalle de |x| si les valeurs de |y| ne font que diminuer.
On lit la variation d'une fonction sur un graphique de la gauche vers la droite.
Soit le graphique suivant :
La fonction est croissante sur l'intervalle |[0,4]|. Elle est strictement croissante sur l'intervalle |[0,2]|.
La fonction est décroissante sur l'intervalle |[2,8]|. Elle est strictement décroissante sur l'intervalle |[4,8]|.
La fonction est constante sur l'intervalle |[2,4]|.
On inclut à la fois l'intervalle |[2,4]| dans la croissance et la décroissance. En effet, sur cet intervalle, la fonction a une variation qui est nulle. On élimine cet intervalle de la croissance et de la décroissance lorsqu'on parle de croissance stricte et de décroissance stricte.
Les extrémums d'une fonction regroupent le maximum et le minimum d'une fonction.
Le maximum d’une fonction correspond à la valeur maximale de son image, c'est-à-dire sa valeur maximale en |y.|
Le minimum d’une fonction correspond à la valeur minimale de son image, c'est-à-dire sa valeur minimale en |y.|
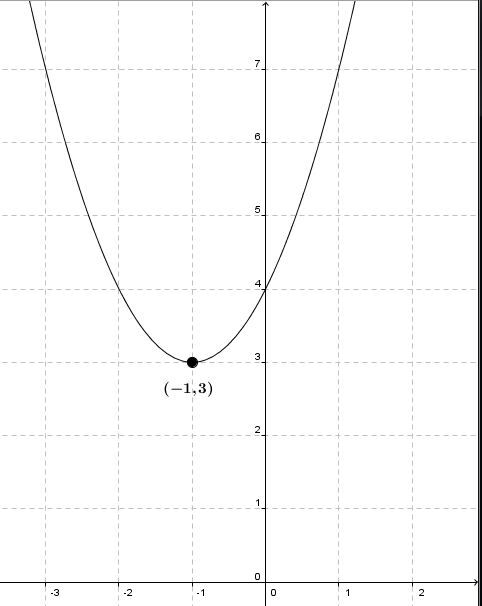
Dans le graphique ci-haut, le minimum est de |3.|
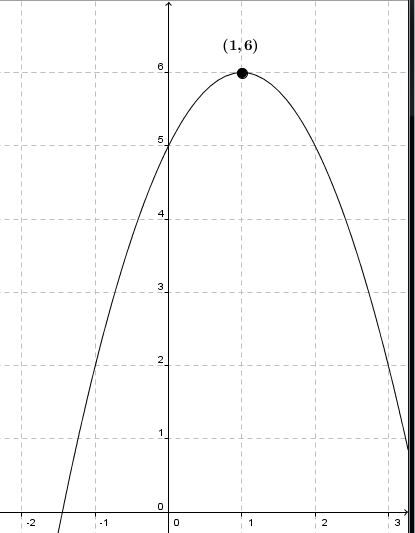
Dans le graphique ci-haut, le maximum est de |6.|
Il se peut qu'une fonction ne possède aucun extrémum. Une fonction peut également posséder un seul extrémum ou en posséder 2.
Afin de déterminer le signe d'une fonction, on regarde les valeurs des ordonnées de cette fonction.
-
On dira qu’une fonction |f(x)| est positive sur un intervalle donné en |x| si, sur cet intervalle, les valeurs de |f(x)| sont supérieures ou égales à 0 (positives).
-
On dira qu’une fonction |f(x)| est négative sur un intervalle donné en |x| si, sur cet intervalle, les valeurs de |f(x)| sont inférieures ou égales à 0 (négatives).
Soit le graphique suivant :
La fonction est positive sur l'intervalle |[-3, + \infty[|.
La fonction est strictement positive sur l'intervalle |]0, +\infty[|.
La fonction est négative sur l'intervalle |]-\infty,0]|.
La fonction est strictement négative sur l'intervalle |]-\infty, -3[|.
L’abscisse à l’origine d'une fonction est la valeur en |x| du point qui se trouve directement sur l’axe des abscisses. En d'autres mots, les coordonnées du point en lien avec l'abscisse à l'origine d'une fonction peuvent s'écrire sous la forme |(x,0).| On parle aussi du zéro de la fonction.
L’ordonnée à l’origine d'une fonction est la valeur en |y| du point qui se trouve directement sur l’axe des ordonnées. Conséquemment, les coordonnées d'un tel point s'écrivent |(0,y)|. On parle aussi de la valeur initiale de la fonction.
Soit le graphique suivant :
L'abscisse à l'origine de la fonction est |-3|.
L'ordonnée à l'origine de la fonction est |3|.
Une fonction possède généralement une seule ordonnée à l'origine. Il peut parfois ne pas y en avoir, mais il ne peut jamais y en avoir plus d'une.
Une fonction peut posséder aucune, une seule ou plusieurs abscisses à l'origine.
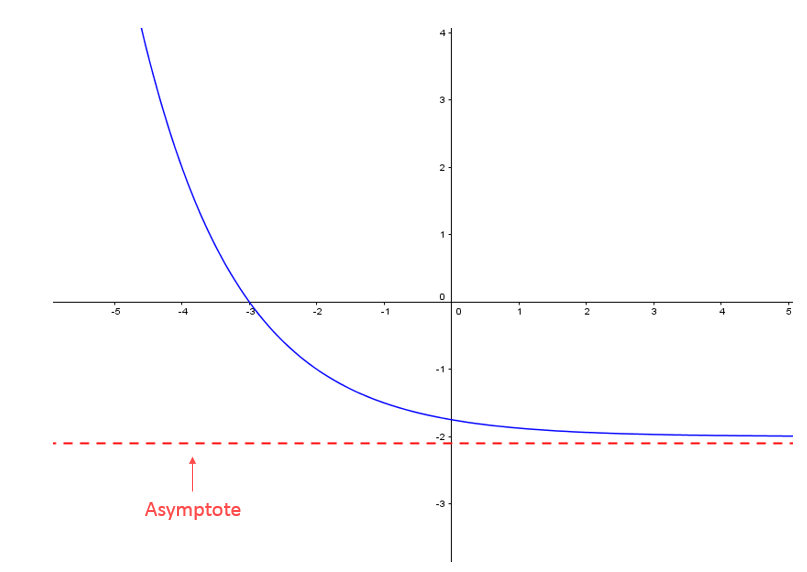
Une asymptote, souvent représentée graphiquement par une ligne pointillée, est une droite vers laquelle s'approche de plus en plus une fonction, sans jamais y toucher. Il peut y avoir plusieurs asymptotes pour une même fonction.
Voici un exemple où la fonction possède 2 asymptotes.
La fonction suivante ne possède qu'une asymptote.
Pour valider ta compréhension de l'analyse des fonctions de façon interactive, consulte la MiniRécup suivante :
