Une suite est une liste d'éléments placés dans un ordre déterminé.
Lorsqu'une série d'éléments est placée sous forme de liste ordonnée, on parle de suite. Pour qu'il y ait une suite, il doit y avoir un motif répétitif qui explique l'ordre des éléments dans la liste. Il existe plusieurs sortes de suites. Parmi elles, certaines sont numériques puisqu'elles font intervenir des nombres, alors que d'autres ne le sont pas.
Une suite non numérique est une liste d'éléments, autres que des nombres, placés dans un ordre déterminé.
Une suite non numérique peut être formée par une suite de couleurs, de sons, de formes géométriques, de gestes. On la reconnaît lorsqu'un certain motif se répète tout au long de la suite.
La suite ci-dessous est une série de cercles de deux couleurs différentes. On voit qu'il y a une répétition de couleur puisque deux cercles oranges suivent deux cercles bleus et ainsi de suite. Il s'agit donc d'une suite de couleurs.
Tous les motifs ci-dessous sont gris. Toutefois, les trois motifs de départ se répètent une seconde fois dans le même ordre. Il s'agit donc d'une suite de formes géométriques.
À partir de cette succession de lettres, peut-on trouver la lettre qui suivra le deuxième m?
j, f, m, a, m, …
Pour trouver cette lettre, il faut d’abord comprendre la logique de la suite. Quand on y réfléchit, on s’aperçoit que ces lettres correspondent à la première lettre des mois de l’année :
janvier, février, mars, avril, mai, …
Le mois qui suit est évidemment juin. La lettre que l’on cherche est donc j, première lettre du mot.
Une suite numérique est une liste ordonnée de nombres.
Un certain vocabulaire doit être maîtrisé afin de bien comprendre les suites numériques.
- Les nombres composant la suite sont appelés termes.
- Dans une suite numérique, chaque terme occupe une position précise appelée rang.
- Le lien mathématique qui se répète entre chacun des termes de la suite se nomme régularité (ou raison).
Dans une suite, chacun des nombres est appelé un terme. Chaque terme est associé à un rang qui indique sa position dans la suite.

Les suites sont très importantes en mathématiques. Au lieu d’étudier les suites de mots ou de lettres, on y étudie plutôt les suites de nombres. En fonction de la régularité qui est présente dans une suite, on distingue les suites arithmétiques et les suites géométriques.
Lorsque la régularité n'est pas constante, la suite numérique sera dit non arithmétique.
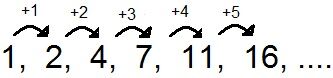
Cette suite est non arithmétique puisque la régularité n'est pas la même entre chaque terme de la suite.
La régularité est le lien qui existe entre les termes d'une suite numérique.
Une suite est composée d'éléments dont la succession dépend d'une régularité. Cette régularité peut être l'addition ou la soustraction d'un nombre, ou la multiplication ou la division d'un terme par un nombre. Ainsi, on peut déterminer, à partir d'un terme donné, d'autres termes dans une suite en ajoutant la régularité au dernier terme de la suite.
On distingue la suite arithmétique et la suite géométrique.
Une suite arithmétique est une suite de nombres dans laquelle la régularité est une addition ou une soustraction d'un nombre.
Lorsque, pour passer d'un terme à l'autre dans une suite, on doit additionner ou soustraire un nombre à chaque terme, on est en présence d'une suite arithmétique. Ainsi, la différence entre deux termes qui se suivent est constante.
Exemples de suites arithmétiques
La régularité de cette suite est -8.
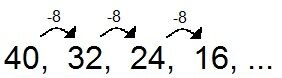
Il serait possible de déduire le prochain terme de la suite : 16 - 8 = 8.
Le prochain terme serait 8.
La régularité de cette suite est +12.
Il serait possible de déduire le prochain terme de la suite : 52 + 12 = 64.
Le prochain terme serait 64.
Pour valider ta compréhension à propos des situations de proportionnalité, des situations inversement proportionnelles et des suites arithmétiques, consulte la MiniRécup suivante.

Une suite géométrique est une suite dans laquelle la régularité est une multiplication ou une division.
Lorsque, pour passer d'un terme à l'autre dans une suite, on doit multiplier ou diviser chaque terme par un même nombre, on est en présence d'une suite géométrique. Ainsi, le rapport entre deux termes consécutifs est une constante.
Exemples de suites géométriques
La régularité de cette suite est x2.
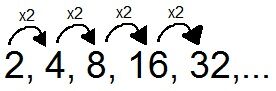
Il serait possible de déduire le prochain terme de la suite : 32 x 2 = 64.
Le prochain terme serait 64.
La régularité de cette suite est ÷3.
Il serait possible de déduire le prochain terme de la suite : 6 ÷ 3 = 2.
Le prochain terme serait 2.
Il exite plusieurs façons de représenter une suite numérique. Dans chacune, le lien entre le rang d'un terme et sa valeur est illustré. Ainsi, on peut décrire une suite de 5 façons distinctes: en mots, à l'aide d'une table de valeurs, par une illustration, par un graphique ou à l'aide d'une règle.
Pour décrire une suite en mots, on donne l'un des termes et on indique sa raison.
Suite: 1, 3, 5, 7, ...
Le premier terme de la suite est 1 et la régularité est +2.
Une table de valeurs met en relation deux valeurs. Dans le cas d'une suite, elle met en relation un rang et un terme.
Suite: 1, 3, 5, 7, ...
Une illustration peut être utilisée pour des suites associées à des constructions géométriques.
Suite: 1, 3, 5, 7, ...
Un graphique met en relation des couples de valeurs à l'aide de points placés dans un plan. Un couple de valeurs peut être formé par un terme (en y) et son rang (en x).
Suite: 1, 3, 5, 7, ...
Graphiquement, une suite arithmétique se caractérise par une suite de points alignés. On peut retrouver trois formes d'alignement.
| Suite arithmétique croissante |
Suite arithmétique décroissante |
Suite arithmétique nulle |
Une règle implique une égalité entre les termes et les rangs.
|t=2n+5\;\;\;\;\;\;|ou|\;\;\;\;\;\;y=3x−1|