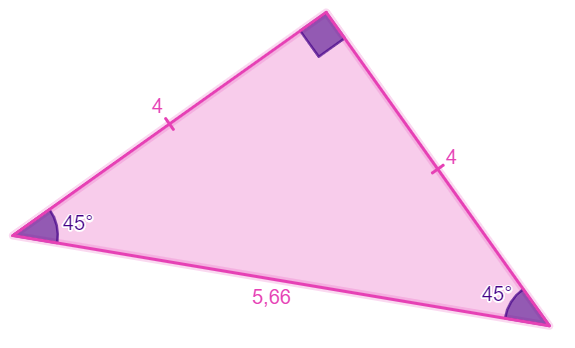
Les triangles sont des polygones composés de trois angles et de trois côtés.
L’origine du mot triangle provient du mot latin triangulus composé du préfixe tri et du mot angulus signifiant respectivement trois et angles. Par ailleurs, les triangles ont certaines particularités qui nous permettent de les classer dépendamment de leurs côtés ou de leurs angles. Pour les dessiner adéquatement, on peut utiliser différentes méthodes de construction.
Par le fait même, le côté le plus petit est opposé à l'angle le plus petit. Ainsi, la longueur du côté d'un triangle influence la mesure de l'angle qui lui est opposé.
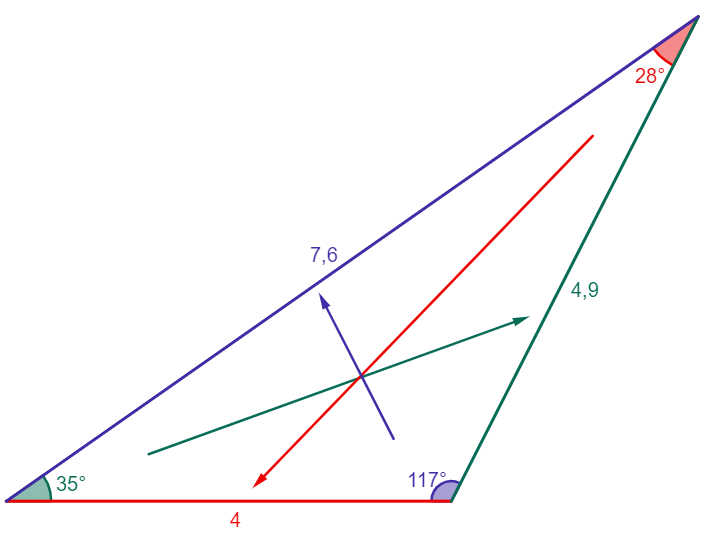
Puisque les triangles sont des polygones, on peut établir une généralité par rapport à la somme des mesures de ses angles intérieurs.
La somme des angles intérieurs d'un triangle est toujours égale à |180^\circ|.
Ainsi, il est possible de déduire la mesure du troisième angle lorsque les mesures des deux autres sont connues.
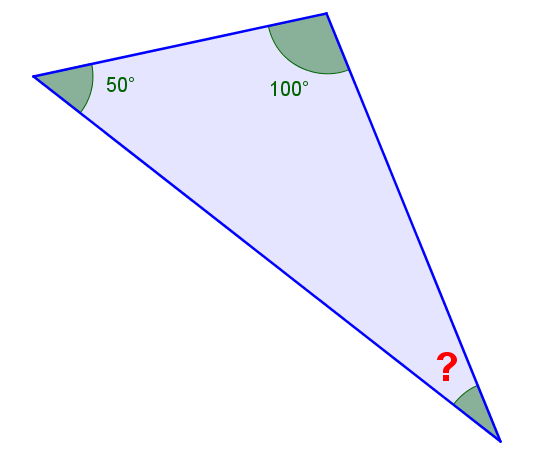
180^\circ &= \text{somme des angles intérieurs} \\
&= 50^\circ + 100^\circ + \color{red}{?} \\
&= 50^\circ + 100^\circ + \color{red}{30^\circ}
\end{align*}||
Ainsi, la mesure de l'angle manquante est |30^\circ|.
Le nom de ce triangle provient de la combinaison du préfixe équi qui signifie égal et latéral qui signifie côté.
Un triangle équilatéral est un triangle dont les trois côtés sont isométriques (de même mesure).
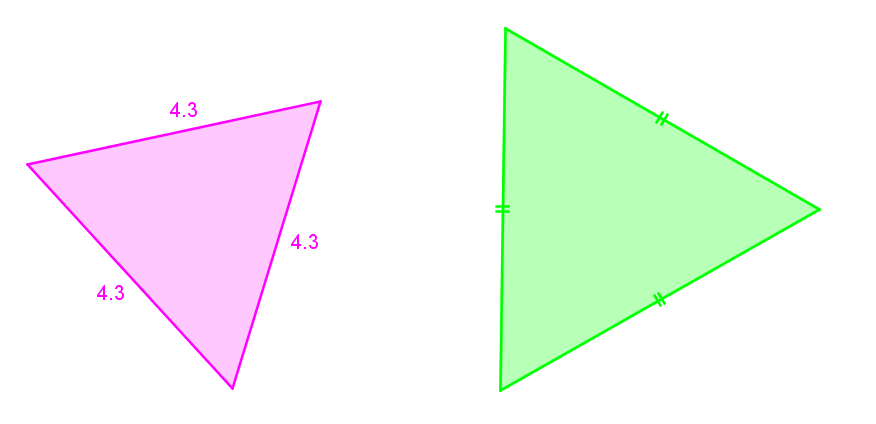
Un triangle équilatéral sera toujours un triangle équiangle puisque tous ses angles seront automatiquement de même mesure.
Le nom de ce triangle provient de la combinaison du préfixe grec isos qui siginifie égal et du mot skêlos qui signifie jambes en grec.
Un triangle isocèle est un triangle dont deux des trois côtés sont isométriques (de même mesure).
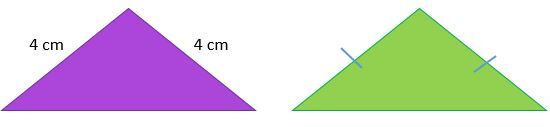
Il est à noter que si des côtés sont «barrés» par le même nombre de traits, alors ces côtés ont la même mesure.
Un triangle isocèle sera toujours un triangle isoangle puisque deux de ses angles seront de même mesure.
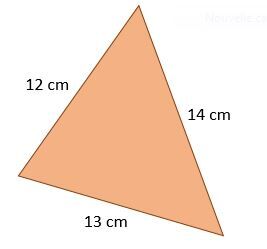
Les mesures d'angles et de côtés d'un triangle scalène ne possèdent aucune caractéristique commune.
Le nom de ce triangle provient de la combinaison du mot latin rectus qui signifie à angle droit et de celui d'angulus qui signifie angle.
Un triangle rectangle est un triangle ayant un angle droit |(90^\circ)| généralement représenté par un carré noir.
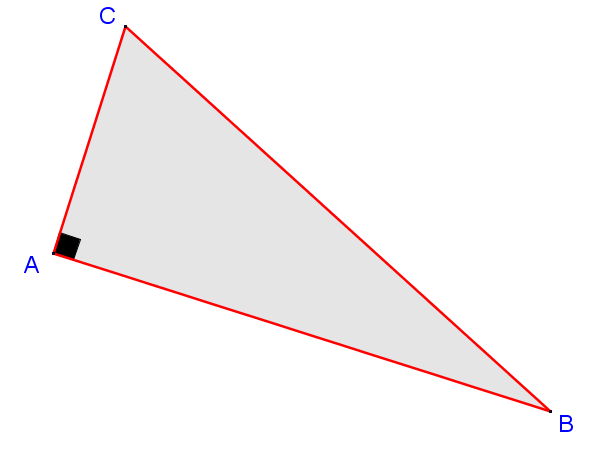
Dans le cas présent, on dira que le triangle |ABC| est rectangle en |A|.
Comme le triangle rectangle est régulièrement utilisé en géométrie, particulièrement dans la relation de Pythagore, on associe un terme bien précis à chacun de ses côtés.
Côté opposé à l'angle de |90^\circ = | hypoténuse
Côtés qui forment l'angle de |90^\circ =| cathètes
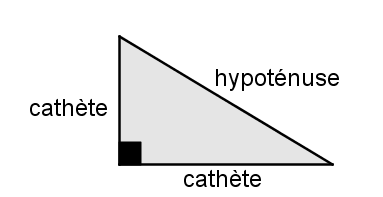
En utilisant la relation de Pythagore, il est possible de trouver des mesures de côtés manquantes.
Le nom de ce triangle provient de la combinaison du préfixe équi qui signifie égal et du mot angle.
Un triangle équiangle est un triangle qui possède trois angles de même mesure.
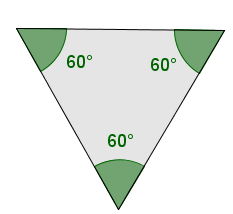
Puisque la somme des angles intérieurs d'un triangle doit être de |180^\circ|, les triangles équiangles possèdent tous trois angles de |60^\circ \ (180^\circ \div 3)|.
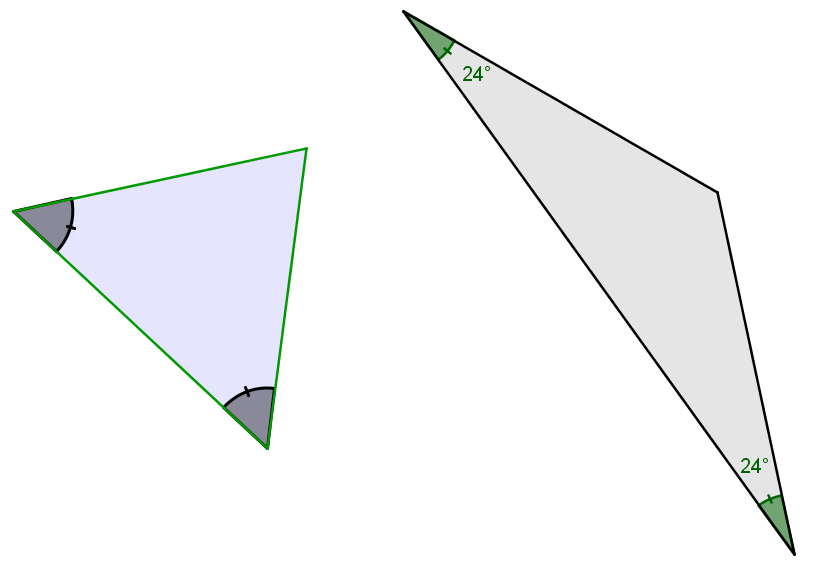
Le nom de ce triangle provient de la combinaison du préfixe grecque isos qui signifie égal et du mot angle.
Un triangle isoangle est un triangle qui possède deux angles de même mesure.
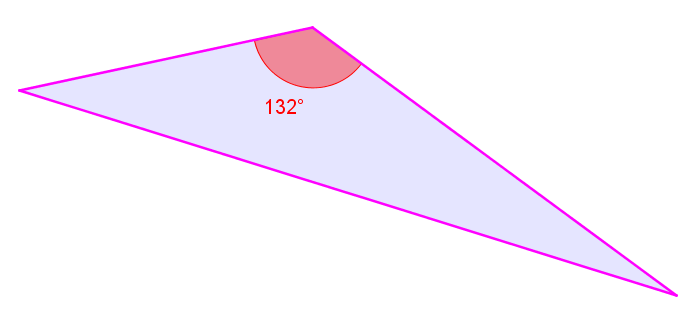
Un triangle obtusangle est un triangle qui possède un angle obtus (supérieur à |90^\circ|).
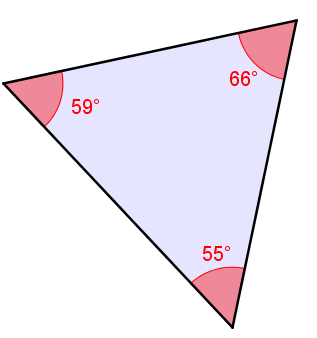
Un triangle acutangle est un triangle formé de trois angles aigus (inférieurs à |90^\circ|).
Dans certains cas, un triangle peut correspondre à plusieurs catégories. On le nommera alors selon ses différentes caractéristiques.
- Triangle acutangle scalène
- Triangle obtusangle isocèle
- Triangle rectangle isocèle