Triangles are polygons composed of three angles and three sides.
The word triangle originates from the Latin word triangulus, composed of the prefix tri and the word angulus, meaning three and angles, respectively. Triangles have certain peculiarities that let us classify them depending on their sides or angles. Different construction methods are used to sketch them.
In any triangle, the longest side is located opposite the largest angle.
Similarly, the smallest side is located opposite the smallest angle. Therefore, the length of the side of a triangle affects the measure of its opposing angle.
Since triangles are polygons, we can state a generalization about the sum of the measures of its interior angles.
The sum of the measures of the interior angles of a triangle always equals |180^\circ.|
As a result, it is possible to deduce the measure of a third angle when the measures of the other two are known.
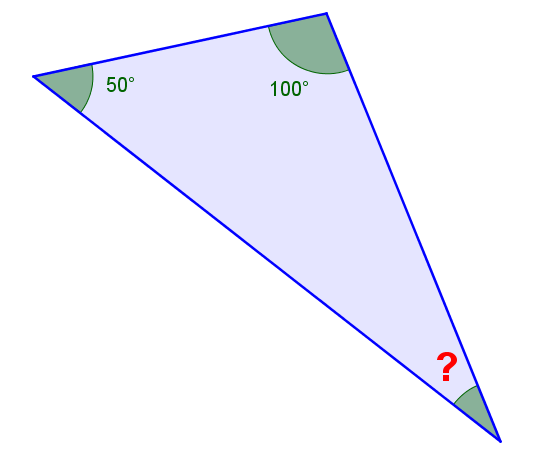
||\begin{align*}
180^\circ &= \text{sum of the interior angles} \\
&=50^\circ+100^\circ+\ \color{#EC0000}{?} \\
&=50^\circ+100^\circ+\color{#EC0000}{30}^\circ
\end{align*}||
The name of this triangle comes from the combination of the prefix equi, which means equal, and lateral, which means side.
An equilateral triangle is a triangle that has three congruent (isometric) sides.

An equilateral triangle will always be an equiangular triangle since all of its angles will necessarily have the same measurement.
The name of this triangle comes from the combination of the Greek prefix isos, which means equal, and the word skelos, which means legs.
An isosceles triangle is a triangle that has both two congruent (isometric) sides and two congruent angles.
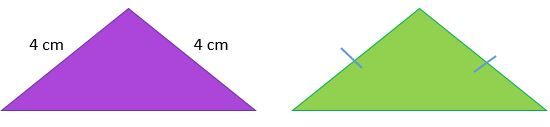
Note that if sides are indicated using the same number of bars, then these sides have the same measurement.
An isosceles triangle will always have two angles with the same measure.
The measurements of all the angles and sides of a scalene triangle are distinct. That is, they all measure differently.
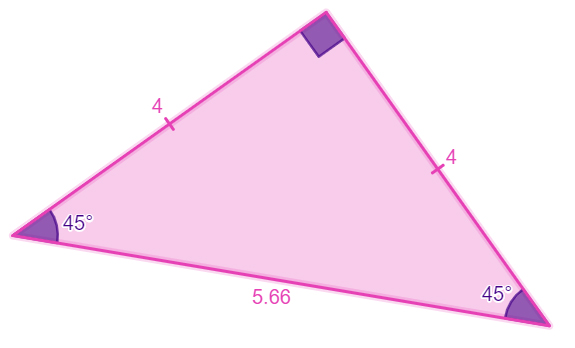
A right triangle is a triangle with one right angle |(90^\circ)| which is generally represented by a black square.
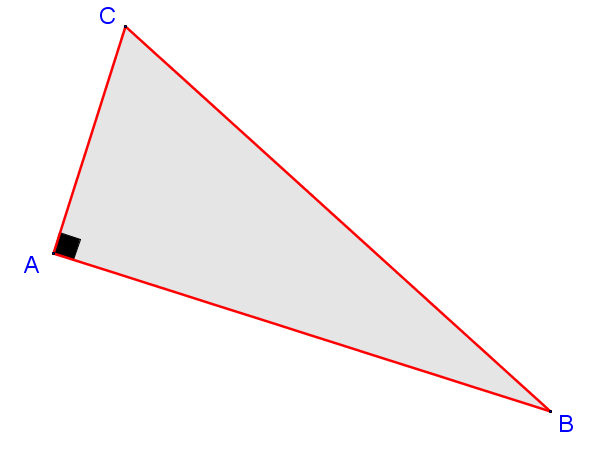
In this case, we would say that triangle |ABC| is right-angled at |A.|
Since the right triangle is regularly used in geometry, particularly when applying the Pythagorean theorem, we associate each of its sides with a precise term.
Side opposite the angle measuring |90^\circ|: hypotenuse
Sides that form the angle measuring |90^\circ|: legs
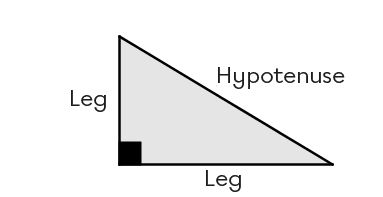
By applying the Pythagorean Theorem, it is possible to find the missing side measurements of a right triangle.
The name of this triangle comes from the combination of the prefix equi, which means equal, and the word angle.
An equiangular triangle is a triangle that has three congruent (equal) angle measurements.
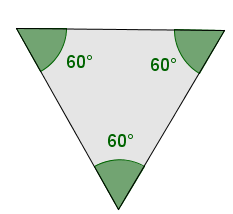
Since the sum of a triangle’s interior angles must be |180^\circ,| equiangular triangles all have three angles of |60^\circ \ (180^\circ \div 3).|
An equiangular triangle will always be an equilateral triangle since all of its sides will automatically have the same measurement.
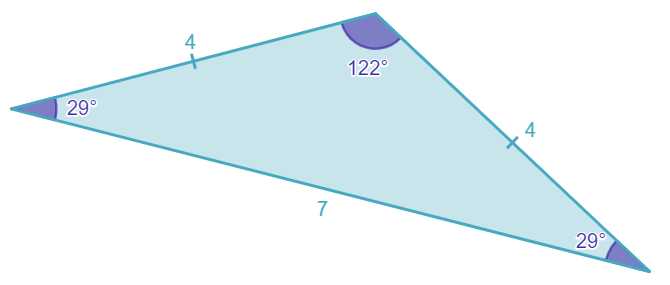
The name of this triangle comes from the combination of the Greek prefix isos, which means equal, and the word skelos, the Greek word for legs.
An isosceles triangle has two angles of equal measure.
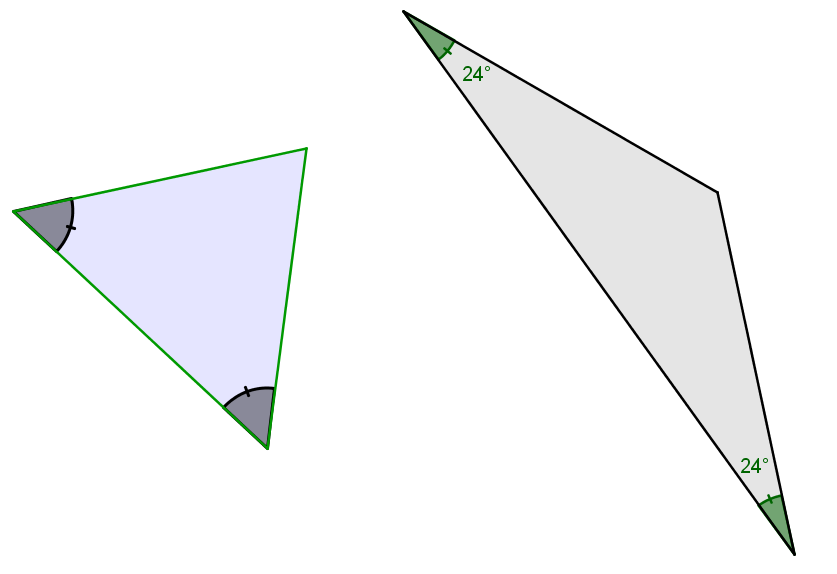
An isosceles triangle will also have two sides of equal measure.
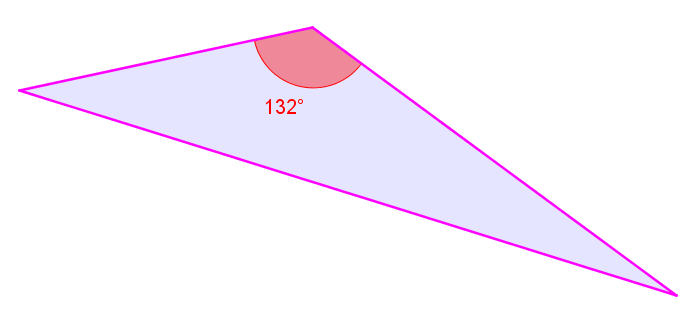
An obtuse triangle is a triangle that has one obtuse angle (greater than |90^\circ|).
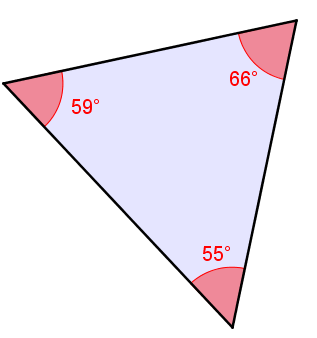
An acute triangle is a triangle formed by three acute angles (less than |90^\circ| ).
Sometimes, a triangle falls into more than one category. In those cases, it is named according to its different characteristics.
-
Scalene acute triangle
-
Obtuse isosceles triangle
-
Isosceles right triangle