L’ensemble des nombres réels, représenté par le symbole |\mathbb{R},| regroupe tous les nombres positifs et négatifs, rationnels ou non, incluant le nombre |0.| Ces nombres peuvent s’écrire à l’aide d’un développement décimal fini ou infini.
L'ensemble des nombres réels correspond à l'union des nombres rationnels |(\mathbb{Q})| et irrationnels |(\mathbb{Q'}| ou |\mathbb{R}\backslash\mathbb{Q}).| Ainsi, tout nombre qui est inclus dans l'ensemble des rationnels ou dans celui des irrationnels fait aussi partie de l'ensemble des nombres réels.||\mathbb{R} = \mathbb{Q} \cup \mathbb{Q}'||
La droite numérique est en fait une représentation de l'ensemble des nombres réels. En d'autres mots, chaque nombre réel peut être représenté par un point sur la droite numérique. C'est pourquoi la droite numérique, qui est continue de |-\infty| à |+\infty,| porte aussi le nom de droite réelle.
Tous les nombres situés sur la droite numérique suivante sont des nombres réels.

En utilisant la notion d'intervalle, l'ensemble des nombres réels peut être représenté de la façon suivante.||x \in \mathbb R \ \text{si}\ x \in\, ]\!-\!\infty,+\infty[||
La somme d’un nombre réel et de son opposé est toujours égale à |0.|
Autrement dit, des nombres opposés sont des nombres qui ont la même valeur absolue, mais qui sont de signes contraires.
-
L’opposé d’un nombre entier
L'opposé de |-6| est |6.| -
L’opposé d’un nombre rationnel en notation fractionnaire
L'opposé de |\dfrac{1}{3}| est |-\dfrac{1}{3}.| -
L’opposé d’un nombre rationnel en notation décimale
L'opposé de |1{,}\overline{3}| est |-1{,}\overline{3}.| -
L’opposé d’un nombre irrationnel
L'opposé de |-\sqrt{2}| est |\sqrt{2}.|
Le produit d’un nombre réel et de son inverse vaut toujours |1.|
Pour déterminer l'inverse d'un nombre, on l’écrit d’abord en notation fractionnaire, puis on inverse le numérateur et le dénominateur.
Remarque : |0| est le seul nombre qui ne possède pas d’inverse.
-
L’inverse d’un nombre naturel
L'inverse de |6| est |\dfrac{1}{6}.| -
L’inverse d’un nombre entier
L'inverse de |-12| est |\dfrac{1}{-12}=-\dfrac{1}{12}.| -
L’inverse d’un nombre rationnel en notation fractionnaire
L’inverse de |\dfrac{7}{10}| est |\dfrac{10}{7}.| -
L’inverse d’un nombre rationnel en notation décimale
L'inverse de |-0{,}2| est |\dfrac{1}{-0{,}2} =\dfrac{1}{-\frac{2}{10}}=\dfrac{10}{-2} =-5.| -
L’inverse d’un nombre irrationnel
L’inverse de |\dfrac{\sqrt{5}}{2}| est |\dfrac{2}{\sqrt{5}}.| Pour éviter de laisser une racine carrée au dénominateur, on rationalise la fraction obtenue.||\dfrac{2}{\sqrt{5}} = \dfrac{2}{\sqrt{5}} \times \dfrac{\sqrt{5}}{\sqrt{5}} = \dfrac{2\sqrt{5}}{5}||
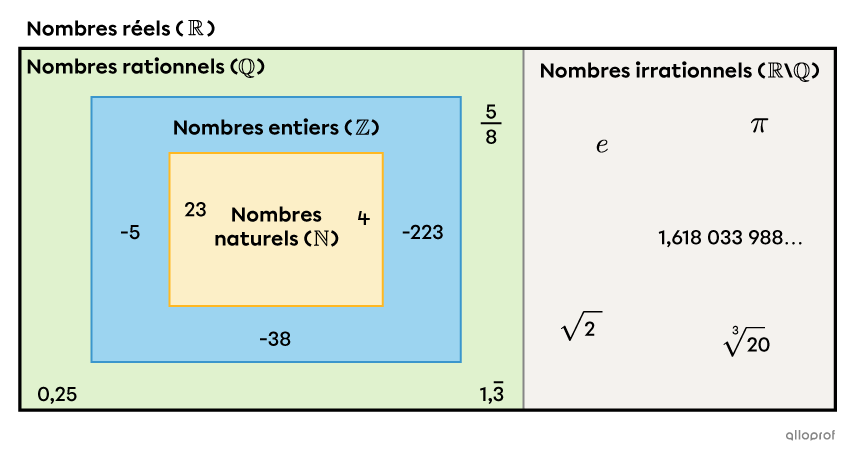
L'ensemble des nombres réels |(\mathbb{R})| est formé de 2 sous-ensembles : les nombres rationnels |(\mathbb{Q})| et les nombres irrationnels |(\mathbb{Q'}| ou |\mathbb{R}\backslash\mathbb{Q}).| ||\mathbb{R}=\mathbb{Q}\cup\mathbb{Q}'||De plus, comme les nombres naturels |(\mathbb{N})| sont inclus dans l’ensemble des nombres entiers |(\mathbb{Z}),| qui est inclus dans celui des rationnels |(\mathbb{Q}),| qui est lui-même inclus dans l’ensemble des nombres réels |(\mathbb{R}),| on a la relation suivante. ||\mathbb N\subset\mathbb Z\subset \mathbb Q\subset \mathbb R||Voici un schéma qui montre l’emplacement de tous les ensembles de nombres dans l'ensemble des nombres réels.
-
Le nombre |4| est un nombre naturel. Il fait aussi partie des entiers. De plus, il est considéré comme un nombre rationnel, car il peut s’écrire sous la forme d’une fraction d’entiers : |\dfrac{4}{1}.| Ainsi, comme |4| fait partie des naturels, des entiers et des rationnels, il fait automatiquement partie des réels.
-
Le nombre |\pi| n’est ni un nombre naturel, ni un nombre entier, ni un nombre rationnel. Toutefois, comme il fait partie des nombres irrationnels, il fait lui aussi partie des nombres réels.
-
En utilisant la notation appropriée, on écrit ceci.||\begin{align}4&\in\mathbb{N}\subset\mathbb Z\subset \mathbb Q\subset \mathbb R\\[3pt] \pi&\in\mathbb{Q}'\subset\mathbb{R}\end{align}||
-
On note |\mathbb{R}^*| l'ensemble des nombres réels dont on a enlevé le nombre |0.|
-
On note |\mathbb {R}_+| l'ensemble des nombres réels positifs.
-
On note |\mathbb {R}_-| l'ensemble des nombres réels négatifs.
-
Il est possible de combiner ces notations. Par exemple, on note |\mathbb{R}^*_-| l’ensemble des nombres réels négatifs sans le nombre |0.|
Pour ordonner des nombres réels, il est utile de les transformer en notation décimale.
Tous les nombres avec lesquels on travaille au secondaire sont des nombres réels.
Toutefois, au-delà des nombres réels, il existe un autre ensemble de nombres, qui se nomme les nombres complexes |(\mathbb{C}).| Ces derniers reposent sur l’existence d’un nombre imaginaire, noté |i,| qui se définit de la façon suivante : |i=\sqrt{-1}.| C’est parce que la racine carrée d’un nombre négatif ne donne pas de solution réelle qu’on dit que |i| est un nombre imaginaire. Les nombres complexes sont très utilisés en physique et dans la plupart des branches de l'ingénierie.