Une équation ou une inéquation logarithmique contient une variable dans l’argument du logarithme.
Pour résoudre une équation logarithmique, il faut être à l'aise avec les lois des logarithmes.
Puisque l’argument d’un logarithme doit être strictement supérieur à |0,| il faut poser des restrictions à la variable de l’équation afin que le ou les logarithme(s) de l’équation aient un argument positif.
Ces restrictions doivent être posées avant de résoudre l’équation logarithmique.
Voici les étapes à suivre pour résoudre une équation logarithmique à une variable.
-
Calculer les restrictions.
-
Réduire l’expression à l’aide des lois des logarithmes, au besoin.
-
Passer à la forme exponentielle.
-
Résoudre l’équation.
-
Valider la ou les solution(s).
-
Donner la solution.
Résous l'équation |\log_2(x+2)=4.|
-
Calculer les restrictions
||\begin{align}x+2&>0\\ x &> -2 \end{align}|| -
Réduire l’expression
L’expression est déjà réduite. -
Passer à la forme exponentielle
||\begin{align}\log_\color{#3B87CD}2(\color{#EC0000}{x+2})&=\color{#3A9A38}4\\ \Updownarrow \\\color{#EC0000}{x+2}&= \color{#3B87CD}2^\color{#3A9A38}4\end{align}|| -
Résoudre l’équation
||\begin{align}x+2 &= 2^4\\ x+2 &= 16\\ x &= 14\end{align}|| -
Valider la solution
La restriction est respectée, car |14>-2.| -
Donner la solution
La solution est |x=14.|
Il y a 2 façons de valider la solution obtenue.
-
S’assurer que la solution respecte la restriction déterminée à l’étape 1, comme le montre l’exemple précédent.
-
Substituer la solution dans l’équation de départ. Dans l’exemple précédent, on remplace la variable |x| dans l’équation de départ et on s’assure que le membre de gauche est équivalent au membre de droite.
||\begin{align}\log_2(\color{#3B87CD}x+2)&=4\\ \log_2(\color{#3B87CD}{14}+2)&\overset{?}{=}4\\ \log_2(16)&\overset{?}{=}4\\ 4&=4\end{align}||La solution est bel et bien valide.
Voici un exemple où l’on doit rejeter l’une des solutions obtenues.
Résous l'équation |\log_6 (x-1) + \log_6 (x) =1.|
-
Calculer les restrictions
Puisque l’équation comporte 2 logarithmes comprenant la variable, on a 2 restrictions à calculer. ||\begin{align}x-1&>0 \\ x&>1\\\\ x&>0\end{align}||On ne retient que |x>1| pour la suite, car cette restriction a priorité sur |x>0.| -
Réduire l’expression à l’aide des lois des logarithmes
Comme les 2 logarithmes ont la même base, on utilise la loi du logarithme d’un produit. ||\begin{align}\log_6 (x-1) + \log_6 (x)&=1\\\ \log_6 \big((x-1)\times x\big)&=1\\ \log_6 (x^2-x)&=1 \end{align}|| -
Passer à la forme exponentielle
||\begin{align}\log_{\color{#3b87cd}6} (\color{#ec0000}{x^2-x})&=\color{#3a9a38}1\\ \Updownarrow\\ \color{#ec0000}{x^2-x}&=\color{#3b87cd}6^\color{#3a9a38}1\end{align}|| -
Résoudre l’équation
||\begin{gather}x^2-x=6^1\\ x^2-x-6=0\\ (x-3)(x+2)=0\\ \overbrace{ \begin{aligned} x-3&=0\\x_1&=3 \end{aligned} \qquad \begin{aligned} x+2&=0\\x_2&=-2 \end{aligned} } \end{gather}|| -
Valider les solutions
La restriction est respectée pour |x_1=3,| car |3>1.| Toutefois, elle n’est pas respectée pour |x_2=-2,| car |-2\not >1.| On rejette |x_2= -2.| -
Donner la solution
La solution est |x=3.|
Voici un exemple où l’équation ne possède aucune solution.
Résous l'équation |\log(x-3)=\log(6x).|
-
Calculer les restrictions
Puisque l’équation comporte 2 logarithmes comprenant la variable, on a 2 restrictions à calculer. ||\begin{align}x-3&>0\\x&>3\\\\ 6x&>0 \\ x&>0\end{align}||On ne retient que |x>3| pour la suite, car cette restriction a priorité sur |x>0.| -
Réduire l’expression à l’aide des lois des logarithmes
||\begin{align}\log (x-3) &= \log (6x)\\ \log (x-3)-\log(6x)&=0\end{align}||Comme les 2 logarithmes ont la même base, on utilise la loi du logarithme d’un quotient. ||\begin{align}\log (x-3)-\log(6x)&=0\\\log \left(\dfrac{x-3}{6x}\right)&=0\end{align}|| -
Passer à la forme exponentielle
Ici, la base du logarithme n’est pas écrite. Quand c’est le cas, par convention, elle vaut 10. ||\begin{align}\log_{\color{#3b87cd}{10}} \left(\color{#ec0000}{\dfrac{x-3}{6x}}\right)&=\color{#3a9a38}0\\ \Updownarrow\\ \color{#ec0000}{\dfrac{x-3}{6x}}&=\color{#3b87cd}{10}^\color{#3a9a38}0\end{align}|| -
Résoudre l’équation
||\begin{align}\dfrac{x-3}{6x}&=10^0\\\dfrac{x-3}{6x}&=1\\x-3&=6x\\-3&=5x\\-0{,}6&=x \end{align}|| -
Valider la solution
La restriction n’est pas respectée, car |-0{,}6\not >3.| Ainsi, il n’y a pas de solution. -
Donner la solution
Cette équation n’a pas de solution.
Voici un exemple où on doit utiliser la formule quadratique pour résoudre l’équation.
Résous l'équation |\log_4 (x^2+14x) = 1.|
-
Calculer les restrictions
||\begin{align} x^2+14x&>0\\ x(x+14)&>0\end{align}||Pour que le produit des facteurs |x| et |(x+14)| soit positif, il faut que ces facteurs soient de même signe. C’est le cas lorsque |x>0| et lorsque |x<-14.| -
Réduire l’expression
L’expression est déjà réduite. -
Passer à la forme exponentielle
||\begin{align}\log_\color{#3b87cd}4 (\color{#ec0000}{x^2+14x})&=\color{#3a9a38}1\\ \Updownarrow\\\color{#ec0000}{x^2+14x} &= \color{#3b87cd}4^\color{#3a9a38}1\end{align}|| -
Résoudre l’équation
||\begin{align}x&^2+14x=4^1\\ x&^2+14x-4=0\\\\ x&= \dfrac{-b\pm \sqrt{b^2- 4ac}}{2a}\\x&= \dfrac{-14\pm \sqrt{14^2- 4(1)(-4)}}{2(1)}\\ x&= \dfrac{-14\pm \sqrt{212}}{2}\\ x_1&\approx 0{,}28 \qquad x_2\approx -14{,}28\end{align}|| -
Valider la solution
Les restrictions sont respectées, car |0{,}28>0| et |-14{,}28<-14.| -
Donner l'ensemble-solution
L'ensemble-solution est |x\in\{-14{,}28; 0{,}28\}.|
Des logarithmes de même base sont égaux si et seulement si les arguments ont la même valeur. ||\log_c (a) = \log_c (b)\ \Leftrightarrow\ a=b||
Résous l'équation |2\log_4 (x) - \log_4 (x+4) = \log_4 (x-2).|
-
Calculer les restrictions
||\begin{align}x&>0\\\\ x+4&>0\\x&>-4\\\\x-2&>0\\x&>2\end{align}||On ne retient que |x>2| pour la suite, car cette restriction a priorité sur |x>-4| et |x>0.| -
Réduire l’expression à l’aide des lois des logarithmes
Pour le premier logarithme, on utilise la loi du logarithme d’une puissance. ||2\log_4 (x)=\log_4(x^2)|| Comme les 2 logarithmes à gauche de l’égalité ont la même base, on utilise la loi du logarithme d’un quotient. ||\begin{align}\log_4 (x^2)-\log_4(x+4)&=\log_4(x-2)\\ \log_4 \left(\dfrac{x^2}{x+4}\right)&=\log_4(x-2)\end{align}||Comme les 2 logarithmes de chaque côté de l’égalité ont la même base, les 2 arguments ont nécessairement la même valeur. On se retrouve avec cette nouvelle équation. ||\dfrac{x^2}{x+4} = x-2|| -
Passer à la forme exponentielle
Dans ce cas, cette étape est inutile. -
Résoudre l’équation
||\begin{align}\dfrac{x^2}{x+4} &= x-2\\ x^2&=(x-2)(x+4)\\x^2&=x^2+2x-8\\0&=2x-8\\-2x&=-8\\x&=4\end{align}|| -
Valider la solution
La restriction est respectée, car |4>2.| -
Donner la solution
La solution est |x=4.|
Résous l’équation |2^{\log_2 5} + 5^{\log_5 3x} = 6^{\log_6 8}.|
-
Calculer les restrictions
Puisque l’équation comporte un seul logarithme comprenant une variable, on a seulement une restriction à calculer. ||\begin{align}3x&>0\\x&>0\end{align}|| -
Réduire l’expression à l’aide des lois des logarithmes
Selon la définition des logarithmes, |\log_2 5| est l’exposant que l’on doit donner à |2| pour obtenir |5.| Puisque cette même expression est en exposant à |2,| on a nécessairement |2^{\log_2 5}=5.| De façon générale, on a |c^{\log_c m} = m.| En appliquant cette identité logarithmique à tous les termes de l’équation, on obtient : ||\begin{align}2^{\log_2 5} + 5^{\log_5 3x}&=6^{\log_6 8}\\5 + 3x &= 8\end{align}|| -
Passer à la forme exponentielle
Dans ce cas, cette étape est inutile. -
Résoudre l’équation
||\begin{align}5 + 3x &= 8\\3x&=3\\x&=1\end{align}|| -
Valider la solution
La restriction est respectée, car |1>0.| -
Donner la solution
La solution est |x=1.|
La résolution d'une inéquation logarithmique est très similaire à la résolution d'une équation logarithmique.
-
Remplacer le symbole d’inégalité par le symbole d’égalité.
-
Calculer les restrictions.
-
Réduire l’expression à l’aide des lois des logarithmes, au besoin.
-
Passer à la forme exponentielle.
-
Résoudre l’équation.
-
Valider la ou les solution(s) de l’équation.
-
Déterminer l’ensemble-solution à l’aide d’un graphique ou d’une droite numérique.
Résous l'inéquation |\log_2 (x-2) \geq 4.|
-
Remplacer le symbole d’inégalité par le symbole d’égalité
||\log_2 (x-2) = 4|| -
Calculer les restrictions
||\begin{align}x-2 &>0\\ x&>2\end{align}|| -
Réduire l’expression
L’expression est déjà réduite. -
Passer à la forme exponentielle
||\begin{align}\log_\color{#3b87cd}2 (\color{#ec0000}{x-2}) &= \color{#3a9a38}4\\\color{#ec0000}{x-2}&=\color{#3b87cd}2^\color{#3a9a38}4\end{align}|| -
Résoudre l’équation
||\begin{align}x-2&=2^4\\x-2&=16\\x&=18\end{align}|| -
Valider la solution
La restriction est respectée, car |18>2.| -
Déterminer l’ensemble-solution
Pour déterminer l’ensemble-solution, on peut tracer le graphique de la fonction logarithmique.
On trace la fonction |f(x)=\log_2 (x-2)| et la droite horizontale |\color{#333fb1}{y=4}.| La fonction logarithmique a une asymptote verticale à |x=2,| qui est représentée par la restriction calculée à l’étape 2. On obtient alors les coordonnées du point d’intersection |(18,4),| dont la coordonnée |x| correspond à la solution calculée à l’étape 5.
L’ensemble-solution est la portion de la courbe qui est supérieure ou égale à |y=4.|
Réponse : On peut conclure que l'ensemble-solution de l'inéquation est l'intervalle |[18, +\infty[.|
Remarque : Puisque le signe d’inégalité est |\geq,| la valeur |18| fait partie de l’ensemble-solution.

Pour déterminer l’ensemble-solution (étape 7), il est également possible d’utiliser une droite numérique. Voici comment on peut résoudre l'exemple précédent à l'aide de cette méthode.
On trace une droite numérique et on y place la restriction déterminée à l’étape 2. Comme |x>2,| |2| est exclu, on le représente sur la droite avec un point vide. On place aussi la solution obtenue à l’étape 5. Puisque cette solution est incluse (étant donné que le symbole d’inéquation de départ est |\geq|), on utilise un point plein.
On appelle |2| et |18| des valeurs critiques. Elles séparent la droite en 3 sections : |]-\infty, 2[,| |]2, 18]| et |[18, +\infty[.|

Pour chaque section, il faut remplacer |x| dans l’inéquation de départ par une valeur quelconque de l’intervalle. Si l’inéquation est respectée, l’intervalle fait partie de l’ensemble-solution, si ce n’est pas le cas, il n’en fait pas partie.
-
Pour l’intervalle |]-\infty, 2[,| on remplace |x| par |0.| ||\begin{align}\log_2 (\color{#3b87cd}x-2) \geq 4\\ \log_2 (\color{#3b87cd}0-2) \overset{?}{\geq} 4 \end{align}||On ne peut pas poursuivre la résolution puisque l’argument du logarithme est négatif, ce qui est impossible. Ainsi, l’intervalle |]-\infty, 2[| ne fait pas partie de l’ensemble-solution.
-
Pour l’intervalle |]2, 18],| on remplace |x| par |3.| En faisant les calculs, on arrive à |0 \geq 4,| ce qui est impossible. Ainsi, l’intervalle |]2, 18]| ne fait pas partie de l’ensemble-solution.
-
Pour l’intervalle |[18, +\infty[,| on remplace |x| par |34.| En faisant les calculs, on arrive à |5\geq\ 4,| ce qui est vrai. Ainsi, l’intervalle |[18, +\infty[| fait partie de l’ensemble-solution.
L’ensemble-solution correspond bel et bien à |[18, +\infty[.|
On peut colorier la section qui correspond à l’ensemble-solution.

Résous l'inéquation |- \log_3 (2x-1) + 5 > 2.|
-
Remplacer le symbole d’inégalité par le symbole d’égalité
||- \log_3 (2x-1) + 5=2|| -
Calculer les restrictions
||\begin{align}2x-1&>0\\2x&>1\\x&>\dfrac{1}{2}\end{align}|| -
Réduire l’expression
||\begin{align}-\log_3 (2x-1) + 5&=2\\-\log_3 (2x-1)&=-3\\\log_3 (2x-1)&=3\end{align}|| -
Passer à la forme exponentielle
||\begin{align}\log_\color{#3b87cd}3 (\color{#ec0000}{2x-1})&=\color{#3a9a38}3\\\Updownarrow\\\color{#ec0000}{2x-1}&=\color{#3b87cd}3^\color{#3a9a38}3\end{align}|| -
Résoudre l’équation
||\begin{align}2x-1&=27\\2x&=28\\x&=14\end{align}|| -
Valider la solution
La restriction est respectée, car |14>\dfrac{1}{2}.| -
Déterminer l’ensemble-solution
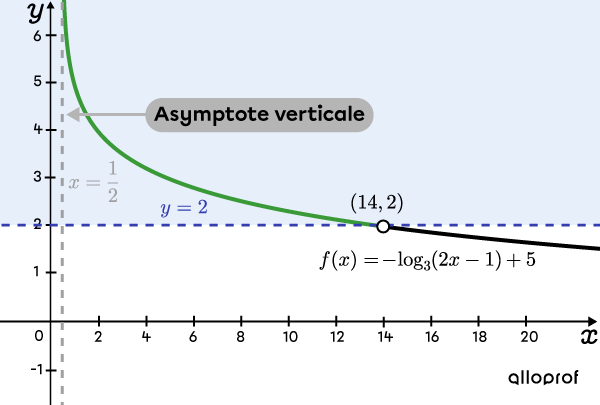
On trace la fonction |f(x)=-\log_3 (2x-1)+5| et la droite horizontale |\color{#333fb1}{y=2}.| La fonction logarithmique a une asymptote verticale à |x=\dfrac{1}{2},| qui est représentée par la restriction calculée à l’étape 2. On remarque l’intersection entre la courbe et la droite au point |(14,2),| ce qui confirme la valeur calculée à l’étape 5.
L’ensemble-solution est la portion de la courbe qui est strictement supérieure à |\color{#333fb1}{y=2}.|
Réponse : On peut conclure que l'ensemble-solution de l'inéquation est l'intervalle |\left]\dfrac{1}{2},14 \right[.|
Remarque : Puisque le signe d’inégalité est |>,| la valeur |14| ne fait pas partie de l’ensemble-solution.