La formule quadratique permet de résoudre une équation polynomiale de degré 2 de la forme |ax^2+bx+c=0| où |a \not= 0.|
||x_{1,2}=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}||
-
Ramener l’équation de degré 2 sous la forme |ax^2+bx+c=0| afin de déterminer |a,| |b| et |c.|
-
Remplacer |a,| |b| et |c| dans la formule quadratique et effectuer le calcul.
-
Donner les solutions.
Lors de la résolution, le symbole |\pm| indique qu’on doit séparer cette formule en 2 : une avec le |+| et l’autre avec le |-.|
||\begin{align}x_1&=\dfrac{-b\color{#ec0000}+\sqrt{b^2-4ac}}{2a}\\\\x_2&=\dfrac{-b\color{#ec0000}-\sqrt{b^2-4ac}}{2a}\end{align}||
Résous l’équation |-5x^2+3{,}5x-1=-4.|
-
Ramener l’équation sous la forme |ax^2+bx+c=0| afin de déterminer |a,| |b| et |c|
||\begin{aligned}-5x^2+3{,}5x-1&=-4\\\color{#ec0000}{-5}x^2+\color{#3b87cd}{3{,}5}x+\color{#3a9a38}3&=0\end{aligned}\\\\
\begin{aligned}\\\color{#ec0000}a=\color{#ec0000}{-5}, \ \color{#3b87cd}b=\color{#3b87cd}{3{,}5},\ \color{#3a9a38}c=\color{#3a9a38}3\end{aligned}|| -
Remplacer |a,| |b| et |c| dans la formule quadratique et effectuer le calcul
||\begin{align}x_{1,2}&=\dfrac{-\color{#3b87cd}b\pm\sqrt{\color{#3b87cd}b^2-4\color{#ec0000}a\color{#3a9a38}c}}{2\color{#ec0000}a}\\&=\dfrac{-\color{#3b87cd}{3{,}5}\pm\sqrt{\color{#3b87cd}{3{,}5}^2-4(\color{#ec0000}{-5})(\color{#3a9a38}3)}}{2(\color{#ec0000}{-5})}\\&=\dfrac{-3{,}5\pm\sqrt{12{,}25+60}}{-10}\\&=\dfrac{-3{,}5\pm\sqrt{72{,}25}}{-10}\\&=\dfrac{-3{,}5\pm8{,}5}{-10}\end{align}|| ||\begin{aligned}x_1&=\dfrac{-3{,}5+8{,}5}{-10} \\&=\dfrac{5}{-10}\\&=-0{,}5\end{aligned}\qquad\begin{aligned}x_2&=\dfrac{-3{,}5-8{,}5}{-10}\\&=\dfrac{-12}{-10}\\&=1{,}2\end{aligned}||
-
Donner les solutions
Les solutions de l’équation |-4=-5x^2+3{,}5x-1| sont |-0{,}5| et |1{,}2.|
Le graphique ci-contre montre que la parabole d’équation |f(x)=-5x^2+3{,}5x-1| croise la droite d’équation |\color{#ff55c3}{y=-4}| à 2 endroits : à |x=-0{,}5| et à |x=1{,}2.|
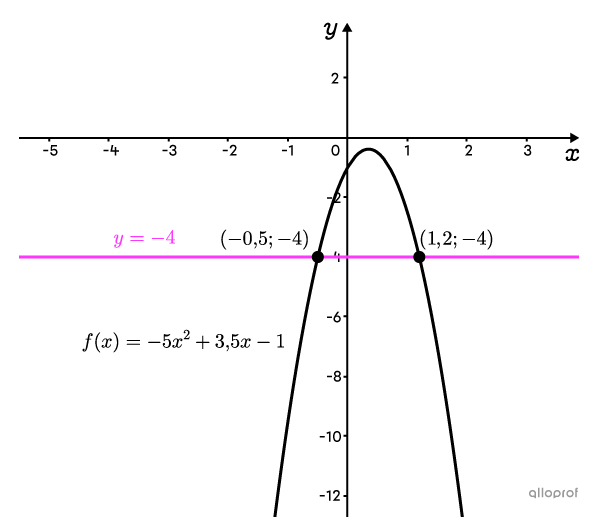
Voici un exemple où on utilise la formule quadratique pour trouver les zéros d’une fonction polynomiale de degré 2.
Trouve les zéros de la fonction polynomiale de degré 2 dont l’équation est |f(x)=-3x^2+8x-10.|
Quand on cherche les zéros d’une fonction, on remplace |f(x)| par |0| et on isole |x.|||\begin{align} f(x)&=-3x^2+8x-10\\0&=-3x^2+8x-10\end{align}||
-
Ramener l’équation sous la forme |ax^2+bx+c=0| afin de déterminer |a,| |b| et |c|
L’équation est déjà sous la bonne forme.||\begin{align}0&=\color{#ec0000}{-3}x^2+\color{#3b87cd}8x\color{#3a9a38}{-10}\\\\ \color{#ec0000}a&=\color{#ec0000}{-3}, \ \color{#3b87cd}b=\color{#3b87cd}{8},\ \color{#3a9a38}c=\color{#3a9a38}{-10}\end{align}|| -
Remplacer |a,| |b| et |c| dans la formule quadratique et effectuer le calcul
||\begin{align}x_{1,2}&=\dfrac{-\color{#3b87cd}b\pm\sqrt{\color{#3b87cd}b^2-4\color{#ec0000}a\color{#3a9a38}c}}{2\color{#ec0000}a}\\
&=\dfrac{-\color{#3b87cd}8\pm\sqrt{\color{#3b87cd}8^2-4(\color{#ec0000}{-3})(\color{#3a9a38}{-10})}}{2(\color{#ec0000}{-3})}\\&=\dfrac{-8\pm\sqrt{64-120}}{-6}\\&=\dfrac{-8\pm\sqrt{-56}}{-6}\end{align}||Comme il est impossible d’extraire la racine carrée d’un nombre négatif, on arrête le calcul ici et on en déduit que la fonction n’a pas de zéro.
-
Donner la solution
La fonction |f(x)=-3x^2+8x-10| n’a pas de zéro.
Le graphique ci-contre montre que la parabole d’équation |f(x)=-3x^2+8x-10| ne croise pas l’axe des |\color{#ff55c3}{x}| puisqu’elle passe complètement en dessous de celui-ci.
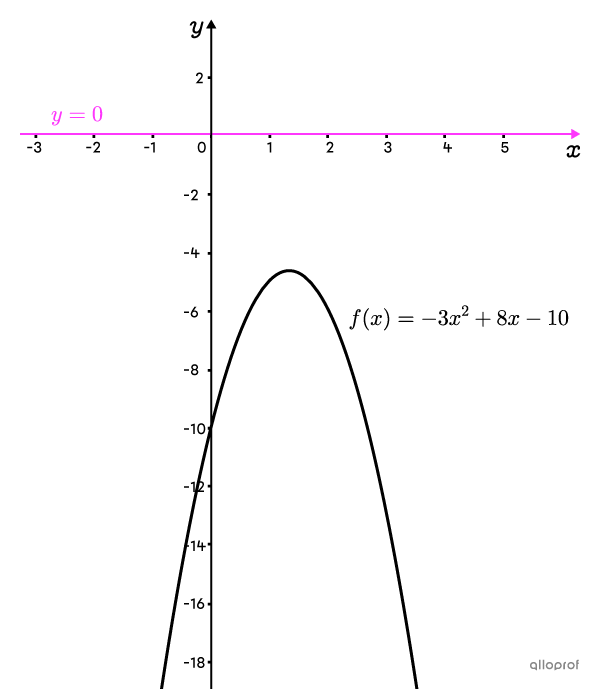
Le discriminant |(\Delta)| est l’expression qui se trouve sous la racine (le radicande) dans la formule quadratique.||\begin{align}x_{1,2}&=\dfrac{-b\pm\sqrt{\color{#333fb1}{\Delta}}}{2a}\\x_{1,2}&=\dfrac{-b\pm\sqrt{\color{#333fb1}{b^2-4ac}}}{2a}\end{align}||Il est important de bien comprendre le lien entre le discriminant du trinôme |ax^2+bx+c| et le nombre de solutions à l’équation |ax^2+bx+c=0.|
|
|b^2-4ac>0| |
L’équation possède 2 solutions distinctes. |
|
|b^2-4ac=0| |
L’équation possède une seule solution. |
|
|b^2-4ac<0| |
L’équation ne possède pas de solution. |
Voici un exemple où l’équation a une solution.
Résous l’équation |2x^2-4x+1=-1.|
-
Ramener l’équation sous la forme |ax^2+bx+c=0| afin de déterminer |a,| |b| et |c|
||\begin{aligned}2x^2-4x+1&=-1\\\color{#ec0000}2x^2\color{#3b87cd}{-4}x+\color{#3a9a38}2&=0\end{aligned}\\\\
\begin{aligned}\\\color{#ec0000}a=\color{#ec0000}{2}, \ \color{#3b87cd}b=\color{#3b87cd}{-4},\ \color{#3a9a38}c=\color{#3a9a38}2\end{aligned}|| -
Remplacer |a,| |b| et |c| dans la formule quadratique et effectuer le calcul
||\begin{align}x_{1,2}&=\dfrac{-\color{#3b87cd}b\pm\sqrt{\color{#3b87cd}b^2-4\color{#ec0000}a\color{#3a9a38}c}}{2\color{#ec0000}a}\\
&=\dfrac{-(\color{#3b87cd}{-4})\pm\sqrt{(\color{#3b87cd}{-4})^2-4(\color{#ec0000}{2})(\color{#3a9a38}{2})}}{2(\color{#ec0000}{2})}\\&=\dfrac{4\pm\sqrt{16-16}}{4}\\&=\dfrac{4\pm\sqrt{0}}{4}\\&=\dfrac{4\pm 0}{4}\\&=\dfrac{4}{4}\\&=1\end{align}||Comme le calcul sous la racine carrée donne |0,| on obtient |\pm 0.| Il n’est donc plus nécessaire de séparer l’équation en 2, car elle n’a qu’une seule solution.
-
Donner la solution
La solution de l’équation |2x^2-4x+1=-1| est |x=1.|
Le graphique ci-contre montre que la droite d’équation |\color{#ff55c3}{y=-1}| passe par le sommet de la parabole |f(x)=2x^2-4x+1.| C’est pourquoi il n’y a qu’une seule solution.

Voici la démonstration de la formule quadratique.
Soit l’équation |ax^2+bx+c=0.| Pour en faire la démonstration, il faut isoler |x.| Pour y arriver, on utilise la complétion du carré. On débute en mettant |a| en évidence.||a\left(x^2+\dfrac{b}{a}x+\dfrac{c}{a}\right)=0||On peut diviser les 2 membres de l'égalité par |a,| car ce dernier est différent de |0.|||x^2+\dfrac{b}{a}x+\dfrac{c}{a}=0||On poursuit en ajoutant et en soustrayant le terme |\left(\dfrac{\frac{b}{a}}{2}\right)^2| à gauche de l’équation. On obtient :||\begin{align}x^2+\dfrac{b}{a}x\color{#3a9a38}{+\left( \dfrac{\frac{b}{a}}{2} \right)^2}+\dfrac{c}{a}\color{#3a9a38}{- \left( \dfrac{\frac{b}{a}}{2} \right)^2}=0\\x^2+\dfrac{b}{a}x\color{#3a9a38}{+\dfrac{b^2}{4a^2}}+\dfrac{c}{a}\color{#3a9a38}{- \dfrac{b^2}{4a^2}}=0\end{align}||Les 3 premiers termes du membre de gauche peuvent être factorisés puisqu'ils forment un trinôme carré parfait.||\left(x+\dfrac{b}{2a}\right)^2+\dfrac{c}{a}-\dfrac{b^2}{4a^2}=0||On met les 2 derniers termes sur un dénominateur commun.||\left(x+\dfrac{b}{2a}\right)^2+\dfrac{4ac-b^2}{4a^2}=0||On soustrait la fraction de chaque côté de l'égalité.
||\left(x+\dfrac{b}{2a}\right)^2=-\left(\dfrac{4ac-b^2}{4a^2}\right)||On distribue le |-| devant la fraction aux 2 termes du numérateur.||\left(x+\dfrac{b}{2a}\right)^2=\dfrac{b^2-4ac}{4a^2}||On extrait la racine carrée des 2 côtés de l'égalité. Il ne faut pas oublier le symbole |\pm| du côté droit.||\begin{align}\color{#ec0000}{\sqrt{\color{black}{\left(x+\dfrac{b}{2a}\right)^2}}} &=\color{#ec0000}{\sqrt{\color{black}{\dfrac{b^2-4ac}{4a^2}}}}\\x+\dfrac{b}{2a}&=\pm \dfrac{\sqrt{b^2-4ac}}{2a}\end{align}||Il ne reste qu’à isoler |x.|||x=-\dfrac{b}{2a}\pm\dfrac{\sqrt{b^2-4ac}}{2a}||On regroupe les 2 fractions.||x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}||On obtient bel et bien la formule quadratique.