Voici les étapes à suivre pour tracer une fonction valeur absolue dans un graphique.
-
Trouver les coordonnées du sommet
Le point le plus important du graphique d’une fonction valeur absolue est sans aucun doute le sommet. Il est donc primordial de trouver les coordonnées de ce sommet pour débuter. Dans |f(x)=a{\mid}x-h{\mid}+k,| les coordonnées du sommet sont |(h,k).|
-
Analyser le signe du paramètre |\boldsymbol{a}|
Si |a| est positif, alors le graphique de la valeur absolue sera ouvert vers le haut.
Au contraire, si |a| est négatif, le graphique de la valeur absolue sera ouvert vers le bas.
-
Calculer l’ordonnée à l’origine
Sous la forme canonique, il nous suffit de remplacer |x| par 0 dans l’équation et de trouver l’ordonnée à l’origine.
-
Calculer les zéros de la fonction
On recherche les valeurs de |x| lorsque |f(x)=0.| Il se peut que la fonction n'ait pas de zéros.
-
Placer les points et tracer la fonction
Soit la fonction suivante : |f(x) = -3 {\mid}x + 4{\mid} +9|
-
Trouver les coordonnées du sommet ||(h,k)=(-4, 9)||
-
Analyser le signe du paramètre |\boldsymbol{a}|
Le paramètre |a| est négatif |(-3).| Donc, la fonction sera tournée vers le bas.
-
Calculer l’ordonnée à l’origine ||\begin{align} f(0) &=-3 {\mid}0 + 4{\mid} + 9 \\ &= -3 {\mid}4{\mid} + 9 \\ &= -3(4) + 9 \\ &= -12 + 9 \\ &= -3 \end{align}||Donc, l'ordonnée à l'origine est |(0,-3).|
-
Calculer les zéros de la fonction ||\begin{align} 0 &= -3 {\mid}x + 4{\mid} + 9 \\ -9 &= -3 {\mid}x + 4{\mid} \\ 3 &= {\mid}x + 4{\mid} \end{align}||
Selon la définition de la valeur absolue, l'intérieur de |{\mid}x + 4{\mid}| peut être positif ou négatif. ||\begin{align} 3 &= x + 4 &\text{et}\quad -3&=x+4 \\ -1 &= x & -7 &= x \end{align}||
Donc, les deux zéros sont |-1| et |-7.|
-
Placer les points et tracer la fonction
On a donc le sommet |(-4,9)| et les points |(0,-3),| |(-1,0)| et |(-7,0).| Ainsi, on peut tracer les 2 demi-droites qui forment la valeur absolue.
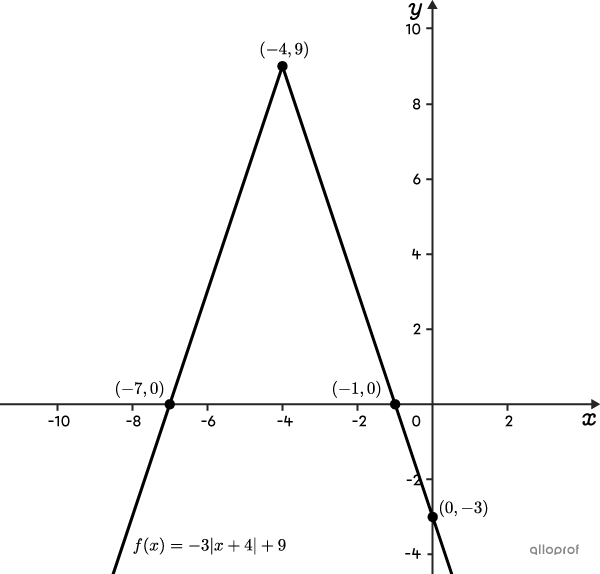
Il n’est pas toujours nécessaire de calculer les zéros de la fonction valeur absolue. Parfois, c’est même impossible.
Par exemple, si les paramètres |k| et |a| sont tous les 2 plus grands que |0,| alors le sommet de la fonction est situé au-dessus de l’axe des |x| et l’ouverture est vers le haut. Les 2 demi-droites ne croisent donc jamais l’axe des |x.|

De la même façon, si |k| et |a| sont tous les 2 négatifs, il n’y a pas de zéros non plus, car les 2 demi-droites sont entièrement en dessous de l’axe des |x.|

Dans ces 2 situations, il est inutile de faire la démarche pour calculer les zéros. On se contente donc de tracer la fonction avec 3 points, soit le sommet et un point sur chaque demi-droite.
Tracez la fonction d'équation |f(x)=2 {\mid}2x + 1{\mid} +1.|
-
Trouver les coordonnées du sommet
Attention! L'équation n'est pas sous la forme canonique. Il faut donc effectuer quelques manipulations.
|f(x) = 2 {\mid}2x+1{\mid} +1 | devient |\begin{align} f(x) = 2 \left\vert 2 \left(x+ \dfrac{1}{2}\right) \right\vert + 1 \end{align}.|
Ainsi, le paramètre |a| vaut 2, le paramètre |b| vaut 2 et les coordonnées du sommet |(h,k)| sont |\left( - \dfrac{1}{2}, 1 \right).| -
Analyser le signe du paramètre |\boldsymbol{a}|
Le paramètre |a| étant positif (il vaut 2), la fonction est ouverte vers le haut. -
Calculer l’ordonnée à l’origine
Nous allons trouver l'ordonnée à l'origine en remplaçant |x| par |0.| ||\begin{align} f(0) &= 2 \left\vert 2 \left(0 + \dfrac{1}{2}\right) \right\vert + 1 \\ f(0) &=3\end{align}||On a donc le point |(0,3).|
On peut utiliser l'axe de symétrie de la fonction. En effet, l'axe de symétrie est |x=h| donc |x=- \dfrac{1}{2}.| On a donc un autre point dont l'ordonnée est |3,| mais avec une abscisse de |-1.| -
Calculer les zéros de la fonction
On remplace |f(x)| par 0. ||\begin{align} 0 &= 2 \left\vert 2 \left(x + \dfrac{1}{2}\right) \right\vert + 1 \\ -1 &= 2 \left\vert 2 \left(x + \dfrac{1}{2}\right) \right\vert \\ -\dfrac{1}{2}&= \left\vert 2 \left(x + \dfrac{1}{2}\right) \right\vert \end{align}||On arrive donc à la conclusion qu'il n'y a pas de zéro puisqu'une valeur absolue ne peut pas être égale à un nombre négatif.
-
Placer les points et tracer la fonction
On a donc le sommet |\left(- \dfrac{1}{2}, 1 \right)| et les points |(0,3)| et |(-1,3).| Ainsi, on peut tracer les 2 demi-droites qui forment la valeur absolue.
