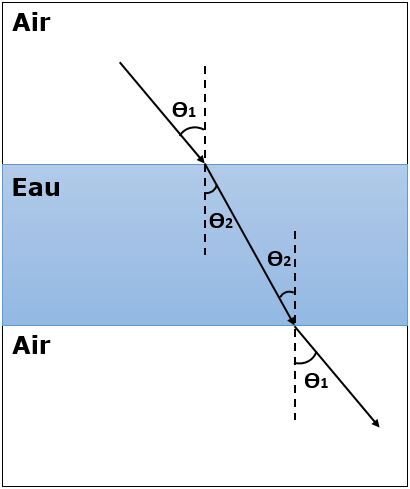
La réfraction est le phénomène lumineux au cours duquel la lumière dévie de sa trajectoire rectiligne en changeant de vitesse lorsqu'elle passe d’un milieu transparent à un autre.
Si un sprinteur court dans un gymnase, sa vitesse sera très élevée. Toutefois, s'il devait faire la même course dans de l'eau, sa vitesse serait nécessairement plus petite, car l'eau ralentirait son mouvement. La lumière agit un peu de la même façon: lorsqu'elle change de milieu, elle diminue sa vitesse et déviera de sa trajectoire.
L’image ci-dessous illustre bien le phénomène.
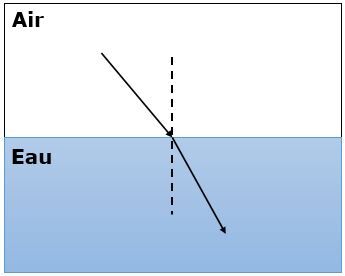
Cette déviation s’explique par le changement de vitesse de la lumière, car la vitesse de la lumière varie d’un milieu transparent à un autre. On dit que ces milieux transparents ont des indices de réfraction différents.
L'indice de réfraction est une valeur indiquant la capacité qu'a une substance à ralentir ou dévier un rayon lumineux.
Pour déterminer un indice de réfraction, il faut comparer la substance transparente à un milieu de référence. Le vide a été choisi comme milieu de référence, puisqu’il s’agit du milieu où la lumière voyage le plus rapidement. Il a été déterminé que l’indice de réfraction absolu du vide serait égal à 1. On compare cette vitesse à celle dans la vitesse dans le second milieu pour établir l'indice de réfraction.
L'équation pour déterminer l’indice de réfraction absolu d’un milieu donné est:
|n= \displaystyle \frac{c}{v}|
où
|n| représente l'indice de réfraction
|c| représente la vitesse de la lumière dans le vide |(c = 3,00 \times 10^{8} \text { m/s})|
|v| représente la vitesse de la lumière dans le milieu donné
L'indice de réfraction n'a pas d'unité de mesure: il représente un facteur indiquant le ralentissement de la lumière dans le milieu par rapport au vide.
Quel est l'indice de réfraction de la glycérine, sachant que la vitesse de la lumière dans ce milieu est |\small 2,04 \times 10^{8} \text {m/s}?|
En utilisant la formule, l'indice de réfraction peut être calculé:
||\begin{align} n= \frac{c}{v} \quad \Rightarrow \quad n &=
\frac{3,00 \times 10^{8}\: \text {m/s}}{2,04 \times 10^{8}\: \text {m/s}} \\ \\
&=1,47 \end{align}||
L'indice de réfraction de la glycérine est donc |1,47|, ce qui signifie que la lumière voyage |1,47| fois plus lentement dans la glycérine que dans le vide.
Voici les indices de réfraction dans quelques milieux.
Indices de réfraction et vitesse de la lumière dans différents milieux
| Milieu | Indice de réfraction | Vitesse de la lumière |\text {(m/s)}| |
| Glace | |1,31| | |2,29 \times 10^{8}| |
| Eau | |1,33| | |2,25 \times 10^{8}| |
| Éthanol | |1,36| | |2,20 \times 10^{8}| |
| Glycérine | |1,47| | |2,04 \times 10^{8}| |
| Huile minérale | |1,48| | |2,02 \times 10^{8}| |
| Pyrex | |1,48| | |2,02 \times 10^{8}| |
| Verre crown | |1,52| | |1,97 \times 10^{8}| |
| Verre flint léger | |1,58| | |1,90 \times 10^{8}| |
| Verre flint | |1,63| | |1,84 \times 10^{8}| |
| Verre flint lourd | |1,66| | |1,81 \times 10^{8}| |
| Diamant | |2,42| | |1,24 \times 10^{8}| |
Plus la lumière se propage rapidement dans un milieu, plus l’indice de réfraction de ce milieu est bas. Ainsi, la lumière voyage plus rapidement dans la glace que dans le diamant.
Lorsque la lumière traverse différents milieux, la déviation sera plus marquée si la différence entre les indices de réfraction est élevée. Comme l'illustre le schéma ci-dessous, la déviation de la lumière est plus grande entre l'air et le verre crown que celle entre le verre crown et l'eau.
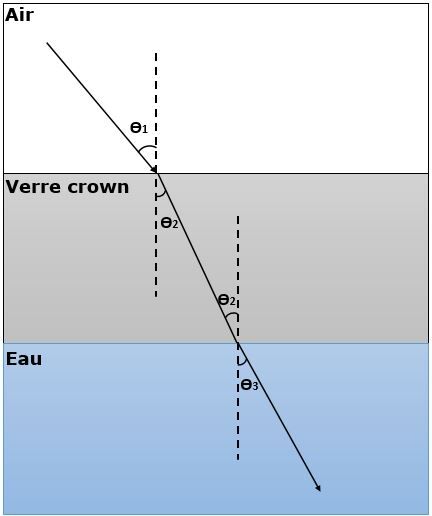
De plus, il est possible de constater que lorsque la lumière passe d'un milieu moins réfringent (ayant un plus petit indice de réfraction) vers un milieu plus réfringent (ayant un plus grand indice de réfraction), le rayon réfracté se rapproche de la normale, comme lorsque la lumière passe de l'air au verre crown dans l'image ci-dessus.
Dans le même ordre d'idées, lorsque la lumière passe d'un milieu plus réfringent vers un milieu moins réfringent, le rayon réfracté s'éloigne de la normale, comme lorsque la lumière passe du verre crown à l'eau dans l'image ci-dessus.
Si les indices de réfraction de deux milieux sont semblables, la lumière agit comme si elle ne traversait qu'un seul milieu.
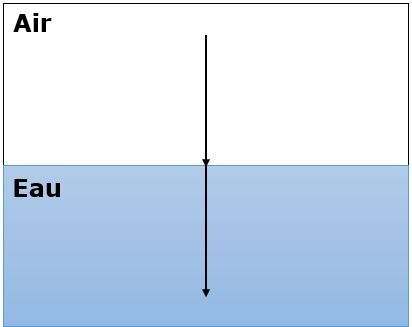
Un rayon qui se dirige vers un milieu transparent perpendiculairement à la surface de ce dernier ne sera pas dévié. Il se déplacera dans le deuxième milieu sans changer d'angle. Toutefois, la vitesse de la lumière diminue quand même bien qu'aucune déviation n'ait été observée.
Un rayon qui passe d'un premier milieu pour se diriger dans un deuxième milieu ayant un indice de réfraction déviera de sa trajectoire. Toutefois, si ce rayon quitte le deuxième milieu pour revenir dans le milieu initial, il reprendra le même angle que celui qu'il avait au départ, à condition que les surfaces séparant les milieux soient parallèles.