La relation entre la position et le temps dans le MRUA est décrite par une relation quadratique durant laquelle la variation de position augmente de plus en plus au fur et à mesure que le temps s'écoule.
Pour observer cette relation, il est pratique de représenter graphiquement des données quant à la position d'un objet en fonction du temps.
Voici le déplacement d'une voiture qui, après s'être arrêtée à un feu rouge, se met en mouvement en fonction du temps.
Déplacement d'une voiture en fonction du temps
| Temps |\small \text {(s)}| | Déplacement |\small \text {(m)}| |
| 0 | 0 |
| 10 | 25 |
| 20 | 100 |
| 30 | 225 |
| 40 | 400 |
| 50 | 625 |
On peut représenter le déplacement de la voiture en fonction du temps dans le graphique ci-dessous.
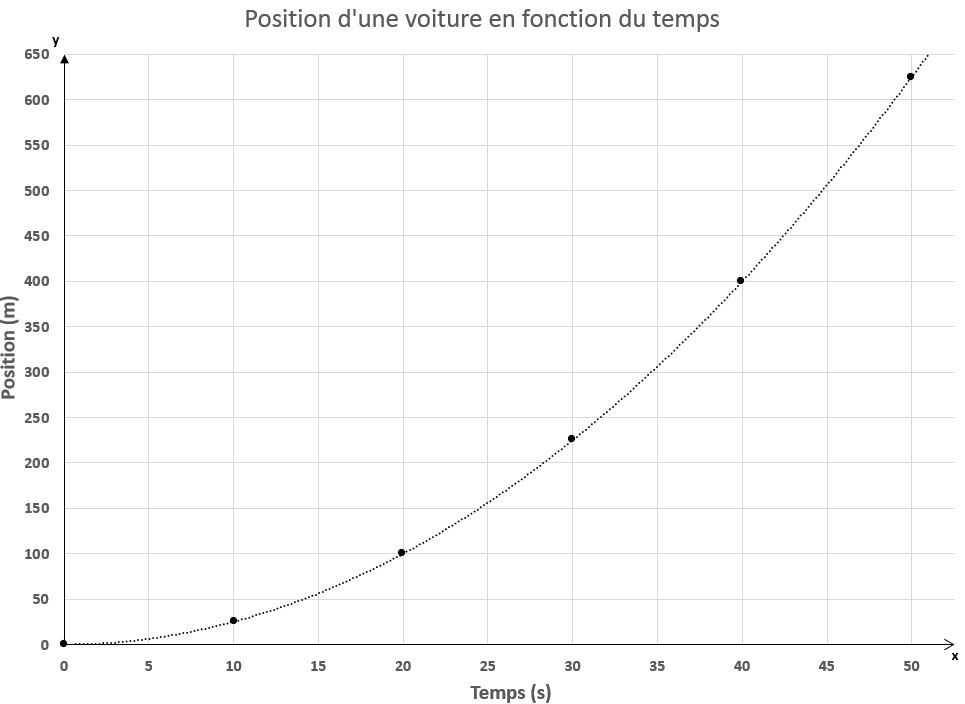
La relation obtenue est une courbe, ce qui signifie que la variation de position est de plus en plus grande pour chaque intervalle de temps.
Même si la relation graphique n'est pas une droite, le calcul d'une pente nous permettrait tout de même de calculer la vitesse de la voiture. En prenant deux points du graphique, il serait possible de déterminer la vitesse moyenne, alors qu'en dessinant la tangente de la courbe en un point donné, on obtiendrait la vitesse instantanée.
Un graphique présentant une relation nulle n'est ni un MRU ni un MRUA. Une droite horizontale signifie que l'objet étudié n'est pas en mouvement: il est immobile.
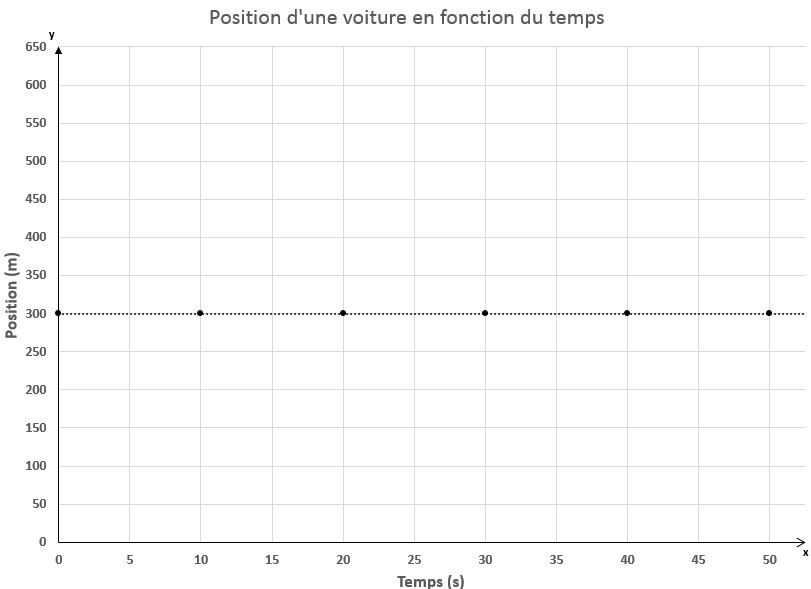
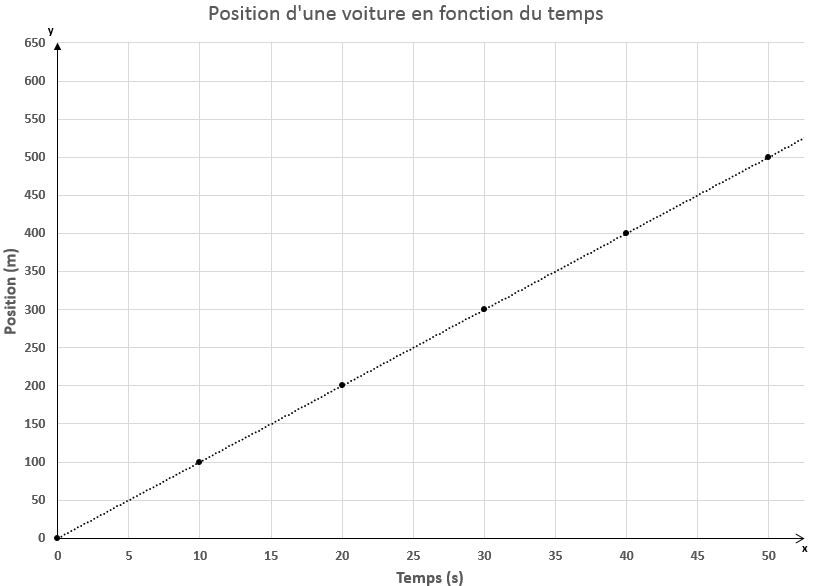
De plus, un graphique présentant une relation linéaire n'est pas un MRUA. Ce type de graphique est caractéristique du MRU.
Pour valider ta compréhension à propos du MRUA de façon interactive, consulte la MiniRécup suivante :

La relation entre la position et le temps dans le MRUA se distingue de la relation entre la position et le temps dans le MRU.