La puissance électrique correspond au travail que peut fournir un appareil électrique à chaque seconde. Plus précisément, la puissance électrique indique la quantité d'énergie qu'un appareil peut transformer durant une période de temps.
L'unité de la puissance est le watt |\text {(W)}|. Elle est mesurée en calculant le produit de la différence de potentiel et de l'intensité du courant dans un circuit.
|P=U \times I|
où
|P| représente la puissance |\text {(W)}|
|U| représente la différence de potentiel |\text {(V)}|
|I| représente l'intensité du courant |\text {(A)}|
Un chauffe-eau fonctionne sous une tension de |\small \text {240 V}| et l’intensité du courant qui y circule est de |\small \text {18,75 A}|. Quelle est la puissance du chauffe-eau?
||\begin{align}U &= \text {240 V} &I &= \text {18,75 A} \\ P &=\ ? \end{align}||||\begin{align}P = U \times I \quad \Rightarrow \quad P &= \text {240 V}\times \text {18,75 A} \\ &= \text {4 500 W} \end{align}|| La puissance du chauffe-eau est |\text {4 500 W}|.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p><span>Un fer à repasser consomme une puissance de |\small \text {1 200 W}|. Sachant que l'intensité du courant dans le circuit électrique est |\small \text {10 A}|, quelle est la résistance de cet élément?<br>
Pour trouver la résistance à partir de la <a href="/fr/eleves/bv/sciences/la-loi-d-ohm-s1164">loi d'Ohm</a>, il faut tout d'abord déterminer la tension.<br>
||\begin{align}P &= \text {1 200 W} &I &= \text {10 A} \\ U&=\ ? \end{align}||||\begin{align}P = U \times I \quad \Rightarrow \quad U &= \frac{P}{I} \\ &= \frac{\text {1 200 W}}{\text {10 A}} \\ &= \text {120 V} \end{align}||La loi d'Ohm permet ensuite de déterminer la résistance de l'élément.||\begin{align}U = R \times I \quad \Rightarrow \quad R &= \frac{U}{I} \\ &= \frac{\text {120 V}}{\text {10 A}} \\ &= 12\ \Omega \end{align}|| La résistance de l'élément dans le fer à repasser est |12\ \Omega|.</span></p>
</body></html>
L'énergie électrique représente l'énergie fournie sous forme de courant électrique.
L'unité reconnue par le système international des unités (SI) est le Joule (J). L'énergie électrique est calculée en déterminant le produit de la puissance électrique et du temps d'utilisation.
|E = P \times \triangle t|
où
|E| représente l'énergie électrique |\text {(J)}|
|P| représente la puissance |\text {(W)}|
|{\triangle t}| représente le temps |\text {(s)}|
De cette relation, il est possible de déterminer qu'un appareil puissant utilisé durant une certaine période de temps consommera plus d'énergie qu'un appareil ayant une plus petite puissance utilisé durant la même période de temps.
De plus, pour deux appareils de même puissance, l'appareil qui consommera le plus d'énergie sera celui dont le temps d'utilisation est le plus élevé.
La relation entre la puissance, le temps et l'énergie électrique peut être représentée dans un graphique.
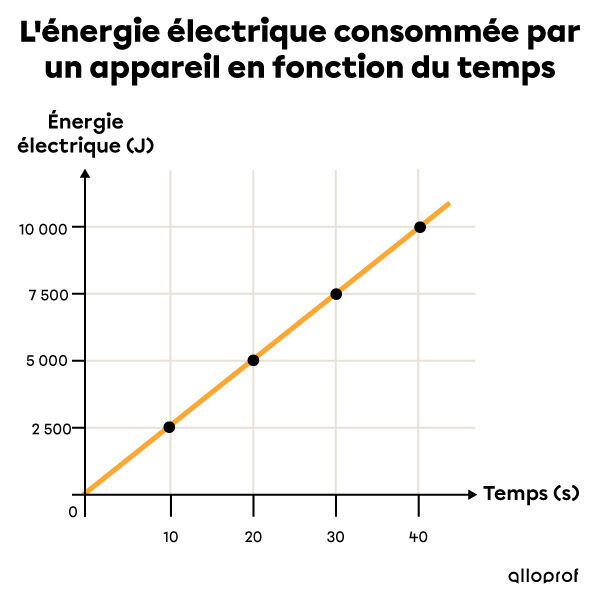
La pente de ce graphique permet de déterminer la puissance de l'appareil.
En utilisant les points |\small (0, 0)| et |\small (40, 10\ 000)|, la pente peut être calculée de la façon suivante.
||\begin{align}E = P \times \triangle t \quad \Rightarrow \quad P &= \frac {E}{\triangle t} \\ P &= \frac {\text {10 000 J - 0 J}}{\text {40 s - 0 s}} \\
P &= \text {250 W} \end{align}||
L'appareil utilisé a une puissance de | \text {250 W}|.
Il est également possible de calculer l'énergie électrique consommée par un appareil en kilowattheures |\small \text {(kWh)}|. Pour ce faire, il faut que la puissance soit transformée en kilowatts et le temps, en heures.
Si la quantité d'énergie en joules a déjà été déterminée, l'équivalence suivante peut être utilisée pour convertir une quantité d'énergie en joules vers les kilowattheures et vice versa.
||\text {1 kWh = 3 600 000 J}||
Vous faites fonctionner un four de |\small \text {2 500 W}| pendant |\small \text {36 minutes}|. Quelle quantité d'énergie électrique, en Joules, sera consommée?
||\begin{align}P &= \text {2 500 W} &\triangle t &= \text {36 min = 2 160 s} \\ E&=\ ? \end{align}||||\begin{align}E = P \times \triangle t \quad \Rightarrow \quad E &= \text {2 500 W} \times \text {2 160 s} \\ &= \text {5 400 000 J} \end{align}|| Le four consommera |\text {5 400 000 J}| d'énergie électrique.
Un micro-ondes de |\small \text {1 100 W}| est utilisé durant trois minutes. Quelle quantité d'énergie électrique, en kilowattheures, sera consommée?
||\begin{align}P &= \text {1 100 W = 1,1 kW} &\triangle t &= \text {3 min = 0,05 h} \\ E&=\ ? \end{align}||||\begin{align}E = P \times \triangle t \quad \Rightarrow \quad E &= \text {1,1 kW} \times \text {0,05 h} \\ &= \text {0,055 kWh} \end{align}|| Le micro-ondes consommera |\text {0,055 kWh}| d'énergie électrique.