Electrical power is the work that an electrical device can perform every second. Specifically, electric power indicates the amount of energy that a device can transform over a period of time.
The power unit is expressed in watts |\text {(W)}|. It is measured by multiplying the potential difference and the current intensity in a circuit.
|P=V \times I|
where
|P\!:| electrical power |\text {(W)}|
|V\!:| potential difference |\text {(V)}|
|I\!:| current intensity |\text {(A)}|
A water heater operates at a voltage of |240\ \text {V}| and the current flowing through it is |18.75\ \text {A}.| What is the electrical power of the water heater?
||\begin{align}V &= 240\ \text {V} &I &= 18.75\ \text {A} \\ P &=\ ? \end{align}||||\begin{align}P = V \times I \quad \Rightarrow \quad P &= 240\ \text {V}\times 18.75\ \text {A} \\ &= 4500\ \text {W} \end{align}|| The power of the water heater is |4500\ \text {W}.|
An iron consumes |1200\ \text {W}| of power. Knowing that the current intensity flowing in the electrical circuit is |10\ \text {A}|, what is the resistance of this element?
To find resistance based on Ohm's law, the voltage must first be determined.
|| \begin {align} P & = 1200\ \text {W} & I & = 10\ \text {A} \\V & = \ ? \end {align} |||| \begin {align} P = V \times I \quad \rightarrow \quad V & = \dfrac {P} {I} \\& = \dfrac {1200\ \text {W}} {10\ \text {A}} \\& = 120\ \text {V} \end {align} || Subsequently, Ohm's law makes it possible to determine the resistance of the element. ||\begin{align}V = R \times I \quad \Rightarrow \quad R &= \frac{V}{I} \\ &= \dfrac{120\ \text {V}}{10\ \text {A}} \\ &= 12\ \Omega \end{align}|| The resistance of the element in the iron is |12\ \Omega.|
Electrical energy is the energy supplied in the form of current intensity.
The unit recognized by the International System of Units (SI) is the joule (J). Electrical energy is calculated by multiplying electrical power and time of use.
|E = P \times \Delta t|
where
|E\!:| electrical energy |\text {(J)}|
|P\!:| electrical power |\text {(W)}|
|\Delta t\!:| time |\text {(s)}|
From this equation, it can be determined that a powerful device used during a certain period of time will consume more energy than a device with a less powerful rating used for the same duration.
Furthermore, for two devices of the same power, the device that consumes the most energy will be the one that is used for a longer time.
The relationship between power, time, and electrical energy can be represented in a graph.
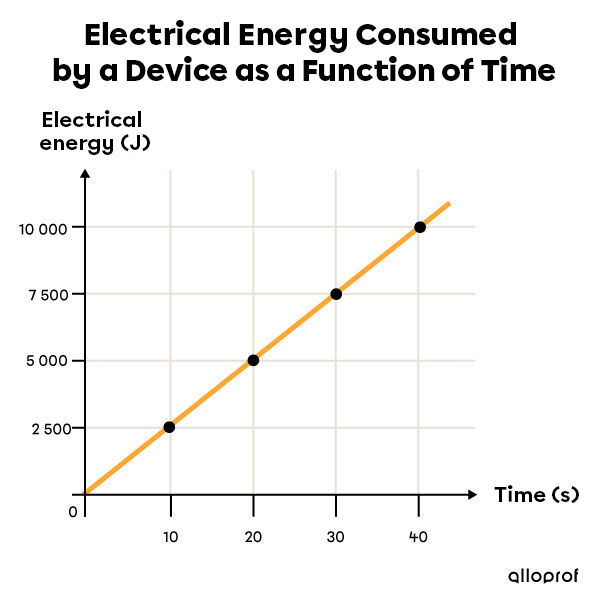
The slope of this line allows us to calculate the electrical power of the appliance.
Using the points |(0, 0)| and |(40, 10\ 000),| the slope can be calculated as follows.
||\begin{align}E = P \times \Delta t \quad \Rightarrow \quad P &= \dfrac {E}{\Delta t} \\ P &= \dfrac {\text {10 000 J - 0 J}}{\text {40 s - 0 s}} \\
P &= \text {250 W} \end{align}||
The device used has a power of |\text {250 W}.|
It is also possible to calculate the electrical energy consumed by a device in kilowatt-hours |\text {(kWh)}.| To do this, the power must be transformed into kilowatts and the time into hours.
If the amount of energy in joules has already been determined, the following equivalence can be used to convert an amount of energy in joules to kilowatt-hours and vice versa.
||\text {1 kWh = 3 600 000 J}||
When heating an oven with a power of |\text {2500 W}| for |\text {36 minutes},| how much electrical energy, in joules, will be consumed?
|| \begin {align} P & = \text {2500 W} & \Delta t & = \text {36 min = 2 160 s} \\E & = \ ? \end {align} |||| \begin {align} E = P \times \Delta t \quad \rightarrow \quad E & = \text {2500 W} \times \text {2160 s} \\& = \text {5 400 000 J} \end {align} || The oven will consume | \text {5 400 000 J} | of electrical energy.
A microwave with a power of |\text {1100 W}| is used for three minutes. How much electrical energy, in kilowatt-hours, will be consumed?
|| \begin {align} P & = \text {1100 W = 1.1 kW} & \Delta t & = \text {3 min = 0.05 h} \\E & = \ ? \end {align} |||| \begin {align} E = P \times \Delta t \quad \rightarrow \quad E & = \text {1.1 kW} \times \text {0.05 h} \\& = \text {0.055 kWh} \end {align} || The microwave will consume | \text {0.055 kWh}| of electrical energy.