Le champ électrique est une zone d’influence invisible qui s’étend autour d’une charge électrique. L’intensité du champ électrique augmente en s’approchant d'une charge électrique et elle diminue en s’en éloignant.
Le champ électrique est la région de l’espace où une charge électrique peut en influencer une autre.
On représente un champ électrique à l’aide de flèches infinies appelées lignes de champ électrique. La direction des lignes de champ électrique indique la direction du mouvement qu’aurait une particule positive placée dans ce champ électrique.
Dans les images suivantes, on représente le champ électrique autour de particules chargées et le champ électrique autour de plaques chargées.

La direction des lignes de champ électrique autour d’une particule positive montre que si l’on plaçait une autre particule positive dans ce champ électrique, elle aurait tendance à s’éloigner de la particule positive.
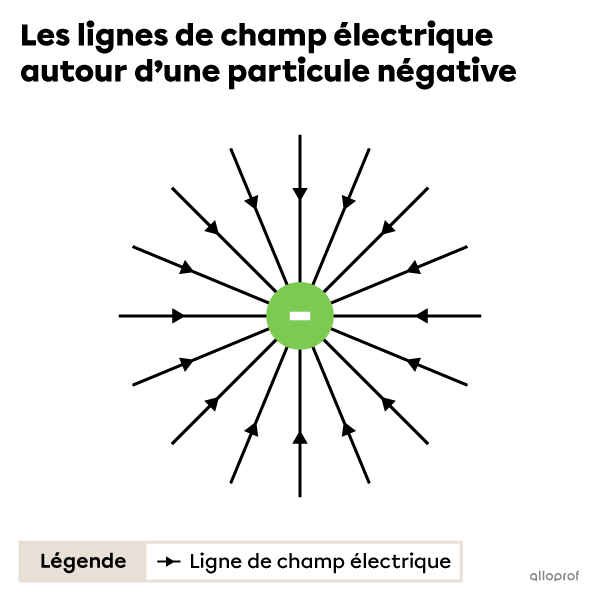
La direction des lignes de champ électrique autour d’une particule négative montre que si l’on plaçait une particule positive dans ce champ électrique, elle aurait tendance à s’approcher de la particule négative.

La direction des lignes de champ électrique autour d’une plaque positive montre que si l’on plaçait une particule positive dans ce champ électrique, elle aurait tendance à s’éloigner de la plaque.

La direction des lignes de champ électrique autour d’une plaque négative montre que si l’on plaçait une particule positive dans ce champ électrique, elle aurait tendance à s’approcher de la plaque.
-
Les lignes de champ électrique s’éloignent des charges positives et se dirigent vers les charges négatives.
-
Les lignes de champ électrique ne se croisent jamais entre elles.
-
Les lignes de champ électrique sont rapprochées les unes des autres pour représenter un champ électrique plus fort. Elles sont éloignées les unes des autres pour représenter un champ électrique plus faible.
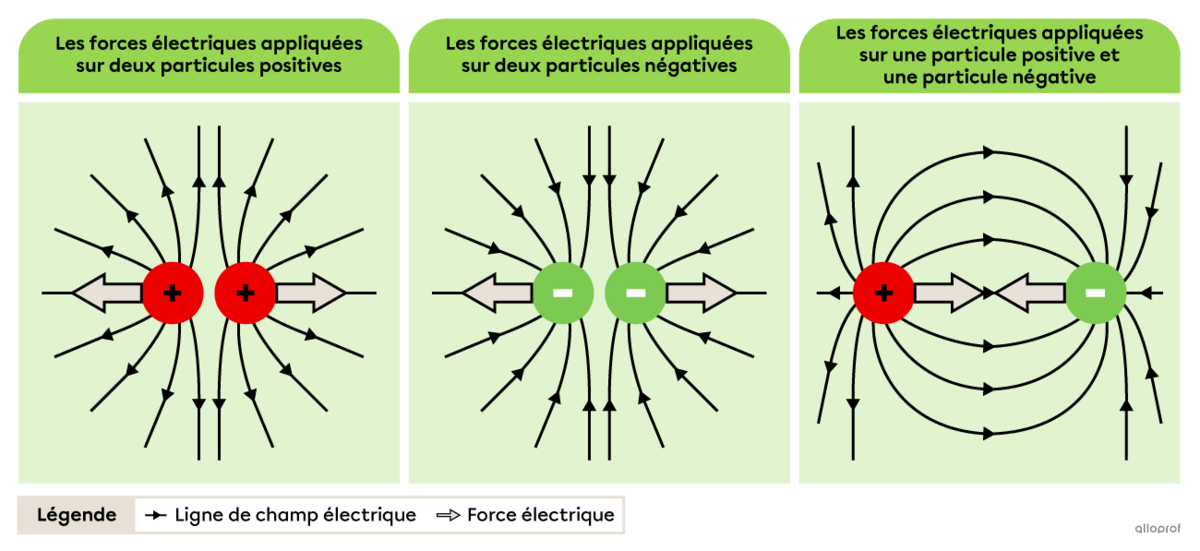
Lorsque deux particules chargées et immobiles sont à proximité l’une de l’autre, chacune des particules interagit avec le champ électrique de l’autre particule. Les deux particules subissent alors une force électrique de même intensité, mais de sens opposé.
-
Les forces électriques appliquées sur deux particules positives sont de même intensité, mais de sens opposé, de façon à ce que les particules soient repoussées l’une par l’autre.
-
Les forces électriques appliquées sur deux particules négatives sont de même intensité, mais de sens opposé, de façon à ce que les particules soient repoussées l’une par l’autre.
-
Les forces électriques appliquées sur une particule positive et une particule négative sont de même intensité, mais de sens opposé, de façon à ce que les particules soient attirées l’une par l’autre.
L’intensité de la force électrique entre deux particules chargées et immobiles peut être calculée à l’aide de la loi de Coulomb.
La loi de Coulomb met en relation l’intensité de la force électrique entre deux particules immobiles, la charge de ces particules et la distance qui les sépare.
-
Plus la charge des particules est grande, plus l’intensité de la force électrique est grande.
-
Plus la distance entre les particules est petite, plus l'intensité de la force électrique est grande.
On calcule l’intensité de la force électrique à l’aide de la formule suivante.
|F_é=\dfrac{kq_1q_2}{r^2}|
où
|F_é\ :| intensité de la force électrique en newtons |(\text{N})|
|k\ :| constante de Coulomb en newtons mètres au carré par coulomb au carré |(9\times 10^9\ \text{Nm}^2/\text{C}^2)|
|q_1\ :| charge de la particule 1 en coulombs |(\text{C})|
|q_2\ :| charge de la particule 2 en coulombs |(\text{C})|
|r\ :| distance entre les particules en mètres |(\text{m})|
-
Si la valeur de |F_é| est positive, cela signifie que les particules ont des charges de même signe, et qu’elles subissent une répulsion.
-
Si la valeur de |F_é| est négative, cela signifie que les particules ont des charges de signe contraire, et qu’elles subissent une attraction.
Détermine l’intensité de la force électrique appliquée sur une particule 1, qui a une charge de |-3{,}2\times10^{-7}\ \text{C},| par une particule 2, qui a une charge de |-5{,}4\times10^{-7}\ \text{C},| si celles-ci sont séparées par une distance de |1{,}0\ \text{m}.|
-
On identifie les données.
||\begin{align}F_é &=\ ?\ \text{N}\\ k &=9\times10^9\ \text{Nm}^2/\text{C}^2\\ q_{1} &=-3{,}2\times10^{-7}\ \text{C}\\ q_{2} &=-5{,}4\times10^{-7}\ \text{C}\\ r &=1{,}0\ \text{m}\end{align}|| -
On détermine la formule à utiliser.
||F_é=\dfrac{kq_1q_2}{r^2}|| -
On remplace les variables, puis on résout l’équation.
||\begin{align}F_é &=\dfrac{9\times10^9\ \text{N}\cancel{\text{m}^2}/\cancel{\text{C}^2}\ \times-3{,}2\times10^{-7}\ \cancel{\text{C}}\ \times-5{,}4\times10^{-7}\ \cancel{\text{C}}}{(1{,}0\ \cancel{\text{m}^2})}\\\\ F_é &\approx1{,}6\times10^{-3}\ \text{N}\end{align}|| -
On répond à la question.
La force électrique entre les deux particules est d’environ |1{,}6\times10^{-3}\ \text{N}.| De plus, puisque |F_é| a une valeur positive, on peut dire que les particules subissent une force de répulsion.
Quelle est la charge d’une particule qui subit une force électrique de |24\ \text{N}| lorsqu’elle est placée à |50\ \text{cm}| d’une autre particule de |2{,}0\times10^{-5}\ \text{C}|?
-
On identifie les données.
Dans cet exemple, les particules chargées 1 et 2 ne sont pas identifiées, alors on peut désigner |q_1| ou |q_2| comme variable inconnue. Ici, c’est la variable |q_1| qui est désignée comme inconnue et |q_2| a une charge de |2{,}0\times10^{-5}\ \text{C}.|
||\begin{align}F_é &=24\ \text{N}\\ k &=9\times10^9\ \text{Nm}^2/\text{C}^2\\ q_{1} &=\ ?\ \text{C}\\ q_{2} &=2{,}0\times10^{-5}\ \text{C}\\ r &=50\ \cancel{\text{cm}}\ \times\dfrac{1\ \text{m}}{100\ \cancel{\text{cm}}}=0{,}50\ \text{m}\end{align}|| -
On détermine la formule à utiliser, puis on isole |q_1.|
||\begin{align}F_é=\dfrac{kq_1q_2}{r^2}\Rightarrow q_1=\dfrac{F_ér^2}{kq_2}\end{align}|| -
On remplace les variables, puis on résout l’équation.
||\begin{align}q_1 &=\dfrac{24\ \cancel{\text{N}}\times(0{,}50\ \cancel{\text{m}})^{\cancel{2}}}{9\times10^9\ \cancel{\text{Nm}^{2}}/\text{C}^{\cancel{2}}\times2{,}0\times10^{-5}\ \cancel{\text{C}}}\\\\ q_1 &\approx3{,}3\times10^{-5}\ \text{C}\end{align}|| -
On répond à la question.
La charge de la particule 1 est d’environ |3{,}3\times10^{-5}\ \text{C}.|
Quelle distance se trouve entre une particule 1 de |2\times10^{-7}\ \text{C}| et une particule 2 de |-2\times10^{-2}\ \text{C}| si la force électrique est de |-4\ \text{N}|?
-
On identifie les données.
||\begin{align}F_{é} &=-4\ \text{N}\\ k &=9\times10^9\ \text{Nm}^2/\text{C}^2\\ q_{1} &=2\times10^{-7}\ \text{C}\\ q_{2} &=-2\times10^{-2}\ \text{C}\\ r &=\ ?\ \text{m}\end{align}|| -
On détermine la formule à utiliser, puis on isole |r.|
||F_{é}=\dfrac{kq_1q_2}{r^2}\Rightarrow r=\sqrt{\dfrac{kq_1q_2}{F_{é}}}|| -
On remplace les variables, puis on résout l’équation.
||\begin{align}r &=\sqrt{\dfrac{9\times10^9\ \cancel{\text{N}}\text{m}^2/\cancel{\text{C}^{2}}\times2\times10^{-7}\ \cancel{\text{C}}\times-2\times10^{-2}\ \cancel{\text{C}}}{-4\ \cancel{\text{N}}}}\\\\r &=3\ \text{m}\end{align}|| -
On répond à la question.
La distance entre les particules est de |3\ \text{m}.|