The electric field is an invisible zone surrounding an electric charge in which the charge can exert an influence on other charges. The intensity of the electric field is strongest near the electric charge and weakens as the distance from the charge increases.
The electric field is the space where one electric charge can influence another.
An electric field is represented by infinite arrows called electric field lines. The direction of the electric field lines indicates the direction of movement that a positive particle placed in this electric field would have.
The following images show the electric field around charged particles and the electric field around charged plates.

The direction of the electric field lines around a positive particle shows that if another positive particle were placed in this electric field, it would move away from the positive particle.
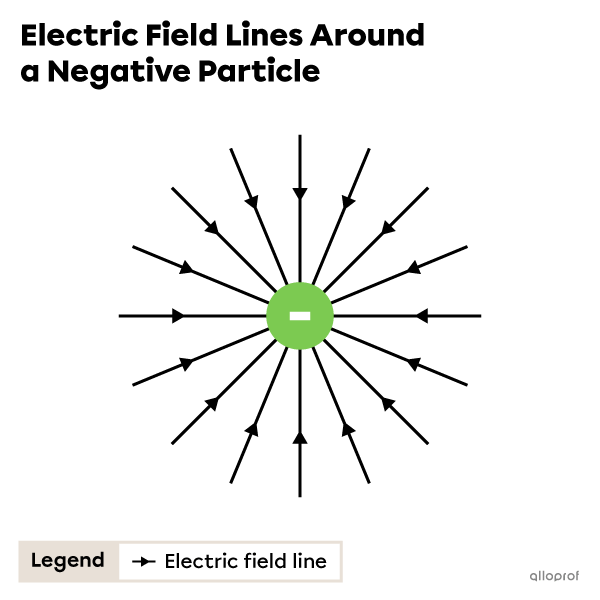
The direction of the electric field lines around a negative particle shows that if a positive particle were placed in this electric field, it would move towards the negative particle.

The direction of the electric field lines around a positive plate shows that if a positive particle were placed in this electric field, it would move away from the plate.

The direction of the electric field lines around a negative plate shows that if a positive particle were placed in this electric field, it would move towards the plate.
-
Electric field lines are oriented away from positive charges and towards negative charges.
-
Electric field lines never cross each other.
-
The electric field lines are close together to represent a stronger electric field. They are further apart to represent a weaker electric field.
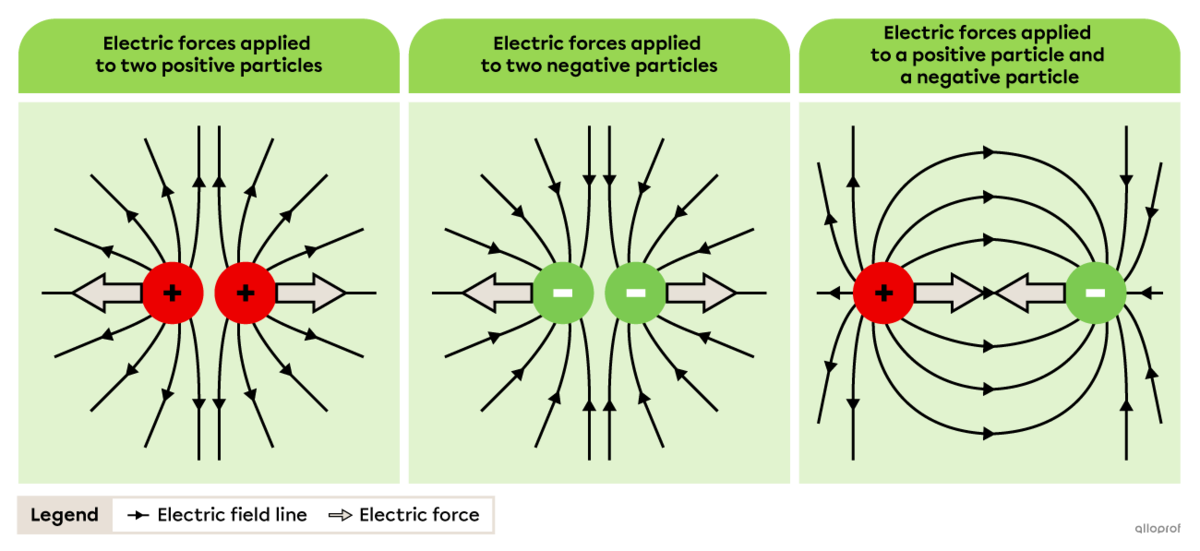
When two charged, immobile particles are close to each other, each particle interacts with the electric field of the other particle. The two particles then experience an electric force of the same intensity, but in the opposite direction.
-
The electric forces applied to two positive particles are of the same intensity, but in opposite directions, so the particles repel each other.
-
The electric forces applied to two negative particles are of the same intensity, but in opposite directions, so the particles repel each other.
-
The electric forces applied to a positive particle and a negative particle are of the same intensity, but in opposite directions, so the particles attract each other.
The strength of the electric force between two immobile charged particles can be calculated using Coulomb's law.
Coulomb's law relates the strength of the electric force between two immobile particles to their charge and to the distance between them.
-
The greater the charge of the particles, the greater the intensity of the electric force.
-
The smaller the distance between the particles, the greater the intensity of the electric force.
On calcule l’intensité de la force électrique à l’aide de la formule suivante.
|F_e=\dfrac{kq_1q_2}{r^2}|
where
|F_e\!:| intensity of the electric force in newtons |(\text{N})|
|k\!:| Coulomb's constant in newtons metres squared per coulombs squared |(9\times 10^9\ \text{Nm}^2/\text{C}^2)|
|q_1\!:| charge of Particle 1 in coulombs |(\text{C})|
|q_2\!:| charge of Particle 2 in coulombs |(\text{C})|
|r\!:| distance between the particles in metres |(\text{m})|
Determine the strength of the electric force applied to Particle 1, which has a charge of |-3.2\times10^{-7}\ \text{C},| by Particle 2, which has a charge of |-5.4\times10^{-7}\ \text{C},| if they are separated by a distance of |1.0\ \text{m}.|
-
First, let’s identify the known values.
||\begin{align}F_e &=\ ?\ \text{N}\\ k &=9\times10^9\ \text{Nm}^2/\text{C}^2\\ q_{1} &=-3.2\times10^{-7}\ \text{C}\\ q_{2} &=-5.4\times10^{-7}\ \text{C}\\ r &=1.0\ \text{m}\end{align}|| -
Choose and write down the formula.
||F_e=\dfrac{kq_1q_2}{r^2}|| -
Replace the variables by the known values and calculate the answer. ||\begin{align}F_e &=\dfrac{9\times10^9\ \text{N}\cancel{\text{m}^2}/\cancel{\text{C}^2}\ \times-3.2\times10^{-7}\ \cancel{\text{C}}\ \times-5.4\times10^{-7}\ \cancel{\text{C}}}{(1.0\ \cancel{\text{m}^2})}\\\\ F_e &\approx1.6\times10^{-3}\ \text{N}\end{align}||
-
The final answer is:
The electrical force between the two particles is approximately |1.6\times10^{-3}\ \text{N}.| In addition, since |F_e| has a positive value, we can say that the particles experience a repulsive force.
What is the charge of a particle which experiences an electric force of |24\ \text{N}| when placed |50\ \text{cm}| away from another particle with a charge of |2.0\times10^{-5}\ \text{C}|?
-
First, let’s identify the known values.
In this example, the charged particles 1 and 2 are not identified, so we can label either |q_1| or |q_2| as unknown. Let’s label |q_1| as the unknown variable and |q_2| as the |2.0\times10^{-5}\ \text{C}| charge.||\begin{align}F_e &=24\ \text{N}\\ k &=9\times10^9\ \text{Nm}^2/\text{C}^2\\ q_{1} &=\ ?\ \text{C}\\ q_{2} &=2.0\times10^{-5}\ \text{C}\\ r &=50\ \cancel{\text{cm}}\ \times\dfrac{1\ \text{m}}{100\ \cancel{\text{cm}}}=0.50\ \text{m}\end{align}|| -
Choose and write down the formula, where the unknown |(q_1)| is isolated.||\begin{align}F_e=\dfrac{kq_1q_2}{r^2}\Rightarrow q_1=\dfrac{F_er^2}{kq_2}\end{align}||
-
Replace the variables by the known values and calculate the answer.
||\begin{align}q_1 &=\dfrac{24\ \cancel{\text{N}}\times(0.50\ \cancel{\text{m}})^{\cancel{2}}}{9\times10^9\ \cancel{\text{Nm}^{2}}/\text{C}^{\cancel{2}}\times2.0\times10^{-5}\ \cancel{\text{C}}}\\\\ q_1 &\approx3.3\times10^{-5}\ \text{C}\end{align}|| -
The final answer is:
The charge of Particle 1 is approximately |3.3\times10^{-5}\ \text{C}.|
What is the distance between Particle 1 of |2\times10^{-7}\ \text{C}| and Particle 2 of |-2\times10^{-2}\ \text{C},| if the electric force is |-4\times10^{-2}\ \text{N}|?
-
First, let’s identify the known values.
||\begin{align}F_e &=-4\ \text{N}\\ k &=9\times10^9\ \text{Nm}^2/\text{C}^2\\ q_{1} &=2\times10^{-7}\ \text{C}\\ q_{2} &=-2\times10^{-2}\ \text{C}\\ r &=\ ?\ \text{m}\end{align}|| -
Choose and write down the formula, where the unknown |(r)| is isolated.
||F_e=\dfrac{kq_1q_2}{r^2}\Rightarrow r=\sqrt{\dfrac{kq_1q_2}{F_e}}|| -
Replace the variables by the known values and calculate the answer.
||\begin{align}r &=\sqrt{\dfrac{9\times10^9\ \cancel{\text{N}}\text{m}^2/\cancel{\text{C}^{2}}\times2\times10^{-7}\ \cancel{\text{C}}\times-2\times10^{-2}\ \cancel{\text{C}}}{-4\ \cancel{\text{N}}}}\\\\r &=3\ \text{m}\end{align}|| -
The final answer is:
The distance between the particles is |3\ \text{m}.|