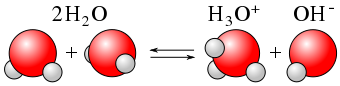
The ionisation constant of water |(K_{water})| is the constant associated with the capacity of water to self-ionise into hydrogen ions |(H^+)| and hydroxide ions |(OH^-)|.
Pure water is a substance that conducts very little current intensity. This electrical conductivity is usually explained by the presence of ions in solution. In fact, it is estimated that only two water molecules in a billion dissociate to form ions.
Water is an amphoteric substance, meaning that it is both an acidity and a basic or alkaline. When a molecule of water dissociates, it forms both a |H^+| ion, which is an acid, and a |OH^-| ion, which is a basic or alkaline. Water auto-ionises when it comes into contact with a second water molecule.
The ionisation of a water molecule is usually represented by the following equation:
|H_{2}O_{(l)} + H_{2}O_{(l)} \rightleftharpoons H_{3}O^{+}_{(aq)} + OH^{-}_{(aq)}|
This equation can be simplified as follows:
|H_{2}O_{(l)} \rightleftharpoons H^{+}_{(aq)} + OH^{-}_{(aq)}|
The ionisation of water is a reversible process, so equilibrium can be reached. Since this system is reversible, we can use the expression for the equilibrium constant of water as follows:
||K_{H_{2}O}=[H_{(aq)}^{+}]\cdot[OH^{-}_{(aq)}]||
This equilibrium constant of water is also called the ionisation constant of water.
It should be remembered that, when calculating an equilibrium constant, we do not take into account the presence of a liquid since its concentration does not vary. This is why the ionisation constant of water is a variation of the equilibrium constant obtained as a function of concentrations in which the reactant (liquid water) does not appear.
During the dissociation of pure water, the concentrations of |[H^{+}_{(aq)}]| and |[OH^{-}_{(aq)}]| are equal since as many |H^{+}_{(aq)}| ions are formed as |OH^{-}_{(aq)}| ions.
As with all equilibrium constants, the value of the ionisation constant of water varies with temperature. At a temperature of 25°C, pure water is neutral and has a pH of 7, so we can deduce that the concentration of |H^{+}| ions is |1\times 10^{-7}|. Consequently, the concentration of |OH^{-}| ions is identical. It is therefore possible to determine the ionisation constant of water as follows:
|K_{H_{2}O} = [H_{(aq)}^{+}]\cdot[OH_{(aq)}^{-}]|
|K_{H_{2}O} = [1\times 10^{-7}]\cdot[1\times 10^{-7}]|
|K_{H_{2}O} = [1\times 10^{-14}]|
Using the expression for the ionisation constant of water, it is possible to calculate the concentration of each of the ions, whether there is an acid or a basic or alkaline in solution. In fact, the product of the concentrations of two ions is always constant (|K_{H_{2}O} = 1\times 10^{-14}|), regardless of what the water contains.
At a temperature of 25°C, 50 ml of an aqueous solution contains a concentration of |OH_{(aq)}^{-}| of |5.0\times 10^{-1} M|. A volume of 250ml of water is added. Determine the value of the final concentration of |H_{(aq)}^{+}|.
Answer:
The dilution phenomenon must first be taken into account, i.e. :
|V_{i}\times C_{i} = V_{f}\times C_{f}|
|50\ ml\times [5.0\times 10^{-1}] = 300\ ml\times [C_{f}]|
|[C_{f}] = [OH_{(aq)}^{-}] = 8.3\times 10^{-2} M|
Then:
|K_{H_{2}O} = [H_{(aq)}^{+}]\times [OH_{(aq)}^{-}]|
|1\times 10^{-14} = [H_{(aq)}^{+}]\times [8.3\times 10^{-2}]|
|\displaystyle [H_{(aq)}^{+}] = \frac{1\times 10^{-14}}{8.3\times 10^{-2}}|
|[H_{(aq)}^{+}] = 1.2\times 10^{-13} M|