A triangle is a kind of plane figure. Calculating its perimeter and area requires certain specific measurements.
To apply these concepts, it is important to know the difference between the perimeter and area of a plane figure.
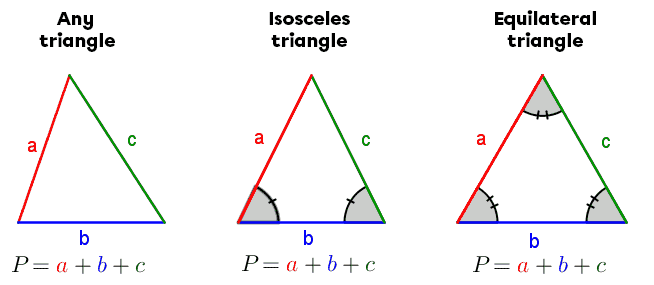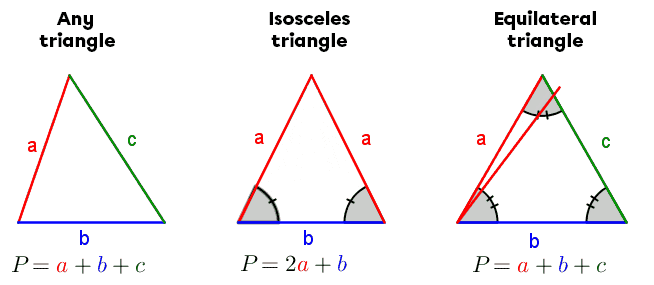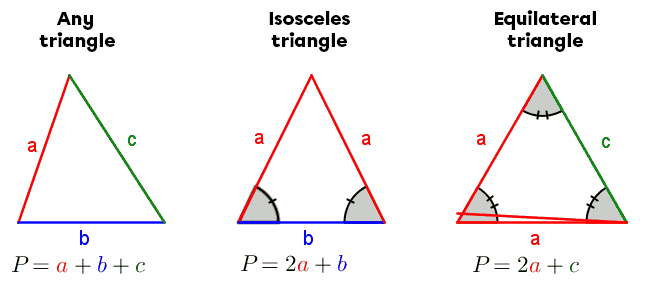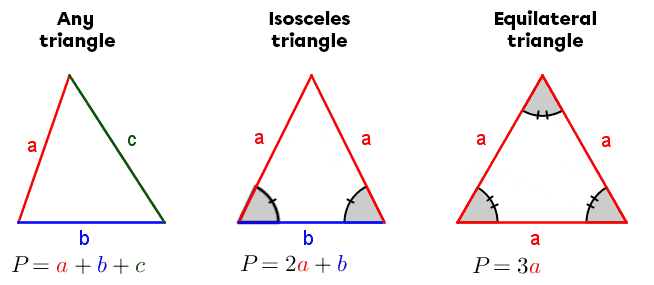
Regardless of the type of triangle, the perimeter can be found by adding up the measurements of all the sides.
||\begin{align*} P_\text{any triangle} &= \color{red}{a} + \color{blue}{b} + \color{green}{c}\\ \\ P_\text{isosceles triangle}&= \color{red}{a} + \color{blue}{b} + \color{green}{c} \\
&= \color{red}{a} + \color{blue}{b} + \color{red}{a} \\
&= 2\color{red}{a} + \color{blue}{b}\\ \\ P_\text{equilateral triangle}&= \color{red}{a} + \color{blue}{b} + \color{green}{c} \\
&= \color{red}{a} + \color{red}{a} + \color{red}{a} \\
&= 3\color{red}{a}
\end{align*}||
So, the precise type of triangle with which we are working can influence the choice of formula to use.
Which of the following two triangles has a larger perimeter?
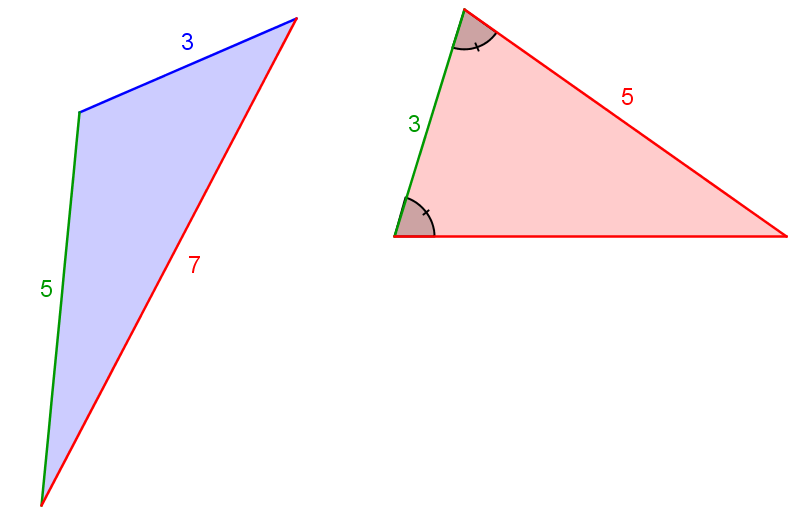
1. If necessary, determine the type of triangle
|\color{blue}{\text{The blue triangle is scalene.}}|
|\color{red}{\text{The red triangle is isosceles.}}|
2. Calculate the perimeter of each triangle using the appropriate formula
||\begin{align*}
\color{blue}{P_\text{scalene triangle}} &= \color{red}{a} + \color{blue}{b} + \color{green}{c} \\
&= \color{red}{7} + \color{blue}{3} + \color{green}{5} \\
&= 15 \ \text{cm} \\
\color{red}{P_\text{isosceles triangle }} & = 2\color{red}{a} + \color{green}{c} \\
&= 2 \color{red}{(5)}+ \color{green}{3} \\
&= 13 \ \text{cm}
\end{align*}||
3. Interpret the answer
Therefore, |\color{blue}{\text{the scalene triangle}}| is the one with the largest perimeter.
The area of a polygon is calculated by determining the area it takes up in square units. In some cases, the area can be found by using a grid and moving some sections of the figure to form "complete squares".

By folding the two small triangles at the end over the middle triangles, the area of the large triangle is found to be |8| square units.
However, this method is often quite tedious. Therefore, it’s preferable to use the formula for the area of a triangle.
||\text{Area}_\text{triangle} = \displaystyle \frac{\color{blue}{b} \color{red}{h}}{2}||
where |\color{blue}{b} \perp \color{red}{h}|

Here, the formula for the area remains the same, regardless of the kind of triangle. However, it is important to remember that the base and the height must be perpendicular.
What will be the price of this advertisement if the director of the event is asking for |\$ 5 / \text{cm}^2|?

1. Identify the base and height
Since the |\color{blue}{18 \ \text{cm}}| side is perpendicular to the |\color{red}{22 \ \text{cm}}| line segment, we find that:
|\color{blue}{\text{base} = 18 \ \text{cm}}|
|\color{red}{\text{height} = 22 \ \text{cm}}|
2. Apply the formula
||\begin{align*}
\text{Area}_\text{triangle} &= \displaystyle \frac{\color{blue}{b} \color{red}{h}}{2} \\
&= \frac{\color{blue}{18} \times \color{red}{22}}{2} \\
&= 198 \ \text{cm}^2
\end{align*}||
3. Interpret the answer
Since the cost of |1 \ \text{cm}^2 = \$ 5|, we have that |198 \ \text{cm}^2 = 198 \times 5 = \$ 990|
As seen in this example, the height is not necessarily vertical. To better understand this, see the definition of height of a polygon.
There are other methods for calculating the area of a triangle, such as the Trigonometric formula and Heron’s formula.