Le triangle est une figure plane dont les calculs du périmètre et de l'aire nécessitent la connaissance de certaines mesures spécifiques.
Afin de bien appliquer ces deux concepts, il est important de connaitre la différence entre le périmètre et l'aire des figures planes .
Peu importe le triangle avec lequel on travaille, on peut toujours calculer son périmètre en additionnant la mesure de tous ses côtés.
||\begin{align*} P_\text{triangle quelconque} &= \color{red}{a} + \color{blue}{b} + \color{green}{c}\\ \\ P_\text{triangle isocèle}&= \color{red}{a} + \color{blue}{b} + \color{green}{c} \\
&= \color{red}{a} + \color{blue}{b} + \color{red}{a} \\
&= 2\color{red}{a} + \color{blue}{b}\\ \\ P_\text{triangle équilatéral}&= \color{red}{a} + \color{blue}{b} + \color{green}{c} \\
&= \color{red}{a} + \color{red}{a} + \color{red}{a} \\
&= 3\color{red}{a}
\end{align*}||

Ainsi, la nature précise du triangle avec lequel on travaille peut influencer le choix de la formule à utiliser.
Lequel des deux triangles suivants a le plus grand périmètre?
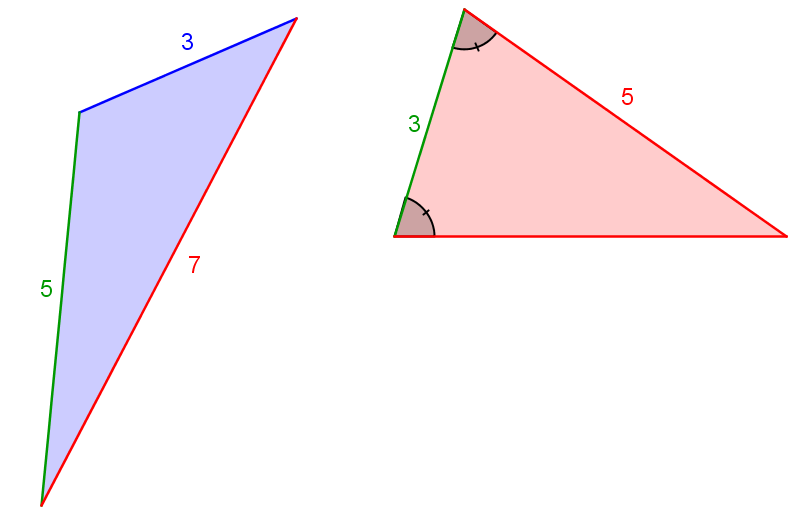
1. Si nécessaire, déterminer la classe des triangles
|\color{blue}{\text{Le triangle bleu est scalène.}}|
|\color{red}{\text{Le triangle rouge est isoangle, donc isocèle.}}|
2. Calculer le périmètre de chacun selon la formule appropriée
||\begin{align*}
\color{blue}{P_\text{triangle scalène}} &= \color{red}{a} + \color{blue}{b} + \color{green}{c} \\
&= \color{red}{7} + \color{blue}{3} + \color{green}{5} \\
&= 15 \ \text{cm} \\
\color{red}{P_\text{triangle isocèle}} & = 2\color{red}{a} + \color{green}{c} \\
&= 2 \color{red}{(5)}+ \color{green}{3} \\
&= 13 \ \text{cm}
\end{align*}||
3. Interpréter la réponse
Ainsi, |\color{blue}{\text{le triangle scalène}}| est celui qui a le plus grand périmètre.
On obtient l'aire d'un polygone en calculant la superficie, en unités carrés, qu'il occupe. Dans certains cas, on peut y arriver en utilisant une feuille quadrillée et en déplaçant certaines sections de la figure pour former des « carrés complets ».

En rabattant les deux petits triangles des extrémités sur les triangles du milieu, on peut déterminer que l'aire du grand triangle initial est de |8| unités carrées.
Par contre, cette méthode est souvent assez fastidieuse. Il est donc préférable d'utiliser la formule associée à l'aire d'un triangle.
||\text{Aire}_\text{triangle} = \displaystyle \frac{\color{blue}{b} \color{red}{h}}{2}||
où |\color{blue}{b} \perp \color{red}{h}|

Dans ce cas-ci, la formule d'aire demeure la même, et ce, peu importe la nature du triangle. Par contre, il est bien important de se rappeler que la base et la hauteur doivent être perpendiculaires.
Quel sera le prix de cet espace publicitaire si le réalisateur de l'évènement demande |5\ $ / \text{cm}^2|?
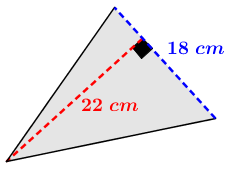
1. Identifier la base et la hauteur
Puisque le côté de |\color{blue}{18 \ \text{cm}}| est perpendiculaire au segment de |\color{red}{22 \ \text{cm}}|, on détermine que :
|\color{blue}{\text{base} = 18 \ \text{cm}}|
|\color{red}{\text{hauteur} = 22 \ \text{cm}}|
2. Appliquer la formule
||\begin{align*}
\text{Aire}_\text{triangle} &= \displaystyle \frac{\color{blue}{b} \color{red}{h}}{2} \\
&= \frac{\color{blue}{18} \times \color{red}{22}}{2} \\
&= 198 \ \text{cm}^2
\end{align*}||
3. Interpréter la réponse
Puisque le cout de |1 \ \text{cm}^2 = 5\ $|, celui de |198 \ \text{cm}^2 = 198 \times 5 = 990\ $|
Par cet exemple, on se rend compte que la hauteur n'est pas obligatoirement représentée par un segment vertical. Pour bien illustrer le tout, on peut se référer à la définition de la hauteur dans un polygone.
D'autres méthodes permettent de calculer l'aire d'un triangle comme la formule trigonométrique et la formule de Héron.