Two types of multiplication can be done with vectors.
To multiply vectors by a scalar, refer to the distributive property of multiplication.
If |k| is a scalar and |\overrightarrow{u}=(a,b)|, then ||k \overrightarrow{u} = k(a,b)=(ka,kb).||
The scalar is sometimes called a scalar quantity. It is a real number that, when multiplied with a vector, changes the magnitude of the vector.
When multiplying a vector by a scalar, the magnitude, or norm, of the resulting vector will be equal to the magnitude of the starting vector multiplied by the absolute value of |k|. So:
-
if | \mid k \mid < 1 \rightarrow|, the magnitude of the resulting vector will be smaller;
-
if | \mid k \mid = 1 \rightarrow |, the magnitude of the resulting vector will be the same;
-
if | \mid k \mid > 1 \rightarrow |, the magnitude of the resulting vector will be larger.
Oftentimes, the main interest is the components of the multiplied vector and not its magnitude.
What are the components of the resultant vector |k \overrightarrow {u}| if |\overrightarrow{u}=(3,-2)| and |k = 5|?
-
Distribute the scalar
||\begin{align} 5 \overrightarrow{u} &= 5 (3, -2) \\
&= (5 \times 3, 5 \times -2) \\
&= (15, -10)\end{align}||
-
Interpret the answer
The product of |5 \overrightarrow {u} = (15, -10).|
Here is the formula for calculating the dot product of two vectors.
If |\overrightarrow{u}=(a,b)| and |\overrightarrow{v}=(c,d)|, then
||\overrightarrow{u}\cdot\overrightarrow{v}=ac+bd.||
Notes: The vectors must be non-zero. This operation is commutative.
From the formula, it is clear that the result of the dot product will be a scalar (a real number). Depending on this scalar, certain characteristics of the two vectors which have been multiplied together can be determined.
For example, the dot product is useful for checking whether two vectors are orthogonal, for calculating work in physics, etc.
Cross product vs dot product
As mentioned, the dot product is written using the symbol |\cdot|. For example, |\overrightarrow{u} \cdot \overrightarrow {v}|.
On the other hand, when the cross (|\times|) is used to write the product of two vectors, the result is called the cross product (a notion usually studied at the college level).
So,
||\overrightarrow {u} \cdot \overrightarrow{v} \neq \overrightarrow {u} \times \overrightarrow {v}||
Coming back to the dot product, here is an example of applying the formula.
What is the dot product of |\overrightarrow{u}=(1,2)| and |\overrightarrow{v}=(3,4)|?
-
Apply the formula
||\begin{align}\overrightarrow{u} \cdot \overrightarrow{v} &= (1,2) \cdot (3,4)\\
&= 1 \times 3 + 2 \times 4\\
&= 3 + 8 \\
&= 11 \end{align}||
-
Interpret the answer
The dot product of |\overrightarrow {u} \cdot \overrightarrow {v} = 11|.
In terms of interpreting the answer, it is difficult to draw important conclusions without any context about the different vectors. The purpose of this example is just to show how to perform the dot product calculation.
There is also another formula to calculate the dot product.
||\overrightarrow{u}\cdot\overrightarrow{v} = {\mid\mid}\overrightarrow{u}{\mid\mid} \times {\mid\mid}\overrightarrow{v}{\mid\mid} \cos \theta||
where |\theta| is the angle in degrees formed by the intersection of the two vectors.
Regardless of the formula used, the final answer and the relationship that can be deduced about the two vectors involved will be the same. However, it is important to choose the right formula according to the information provided in the problem or the information which needs to be found.
Sometimes, both formulas can both be used to solve the problem.
Consider the vector |\overrightarrow{u}=(\color{red}{1},\color{blue}{3})| and the vector |\overrightarrow{v}=(\color{green}{2},4)|.
What is the angle |\theta| formed by these two vectors?
-
Use the first formula for the dot product
||\begin{align} \overrightarrow {u} \cdot \overrightarrow{v} &= \color{red}{a} \times \color{green}{c} + \color{blue}{b} \times d \\
&= \color{red}{1} \times \color{green}{2} + \color{blue}{3} \times 4\\
&= 14 \end{align}||
-
Use the second formula for the dot product
Assuming the tails of each vector coincide with the origin of the Cartesian plane |(0,0)|, their magnitudes can be calculated as follows:
||\begin{align}\mid \mid \overrightarrow{u} \mid \mid &=\sqrt{(1 - 0)^2 + (3-0)^2} \\
&= \sqrt{10} \\
& \\
\mid \mid \overrightarrow{v} \mid \mid &=\sqrt{(2-0)^2 + (4-0)^2}\\
&= \sqrt{20} \end{align}||
So,
||\begin{align}\overrightarrow{u} \cdot \overrightarrow {v} &= {\mid\mid}\overrightarrow{u}{\mid\mid} \times {\mid\mid}\overrightarrow{v}{\mid\mid} \cos \theta \\ &= \sqrt{10}\times \sqrt{20} \cos \theta \\ &= \sqrt{200} \cos \theta \end{align}||
-
Compare the answers
Using both formulas, two different answers were obtained that look fairly different. However, these answers represent the same scalar.
Relating them directly,
||\begin{align} 14 &= \sqrt{200} \cos \theta \\
\frac{14}{\sqrt{200}} &= \cos \theta \\
8.13^\circ &\approx \theta \end{align}|| -
Interpret the answer
The angle between the two vectors is approximately |8.13^\circ.|
After applying this process many times in different contexts and with different vectors, we can make certain observations about the scalar product.
-
|\overrightarrow{u} \cdot \overrightarrow{v} > 0 \rightarrow| the angle |\theta| between the two vectors is acute.
-
|\overrightarrow{u} \cdot \overrightarrow{v} < 0 \rightarrow| the angle |\theta| between the two vectors is obtuse.
-
|\overrightarrow{u} \cdot \overrightarrow{v} = 0 \rightarrow| the angle |\theta| between the two vectors is right.
Let's see how to prove the equivalence of the dot product formulas.
Here is the diagram used for the proof.
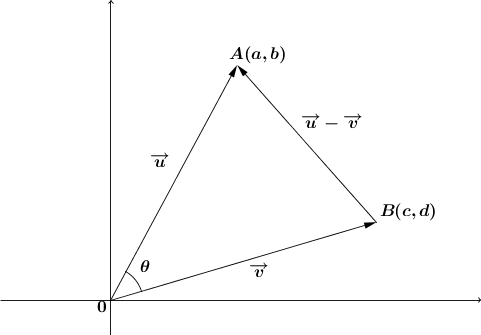
Show that |\overrightarrow{u} \cdot \overrightarrow{v}=ac+bd.|
Use the cosine law to analyze the triangle |OAB.|
||\begin{align}\mid \mid \overrightarrow{u} - \overrightarrow{v} \mid \mid^2 &=\mid \mid \overrightarrow{u}\mid \mid^2 + \mid \mid \overrightarrow{v} \mid \mid^2 - 2 \mid \mid \overrightarrow{u}\mid \mid \times \mid \mid \overrightarrow{v}\mid \mid \cos \theta \\ \Rightarrow \mid \mid \overrightarrow{u} \mid \mid \times \mid \mid \overrightarrow{v} \mid \mid \cos \theta&= \dfrac{1}{2} \left(\mid \mid \overrightarrow{u} \mid \mid^2 + \mid \mid \overrightarrow{v} \mid \mid^2 - \mid \mid \overrightarrow{u}-\overrightarrow{v} \mid \mid^2 \right) \end{align}||
Recall that:
||\begin{align}\overrightarrow{u} \cdot \overrightarrow{v} &= \mid \mid \overrightarrow{u} \mid \mid \times \mid \mid \overrightarrow{v} \mid \mid \cos \theta \\ &= \frac{1}{2} \left(\mid \mid \overrightarrow{u} \mid \mid^2 + \mid \mid \overrightarrow{v} \mid \mid^2 - \mid \mid \overrightarrow{u} - \overrightarrow{v} \mid \mid^2 \right)\end{align}||
Then start expanding the magnitudes of the vectors using the definitions.
||\begin{align} \mid \mid \overrightarrow{u} \mid \mid^2 &= a^2+b^2 \\ \mid \mid \overrightarrow{v} \mid \mid^2 &= c^2+d^2 \\ \mid \mid \overrightarrow{u} - \overrightarrow{v} \mid \mid^2 &= (a-c)^2+(b-d)^2\end{align}||
Substitute:
||\begin{align} \overrightarrow{u} \cdot \overrightarrow{v} &= \frac{1}{2} \left( a^2+b^2 + c^2+d^2 - ((a-c)^2+(b-d)^2) \right) \\
&= \frac{1}{2} \left( a^2 + b^2 + c^2 + d^2 - a^2+2ac-c^2-b^2+2bd-d^2 \right) \\
&= \frac{1}{2} \left( 2ac+2bd \right)\\
&= ac + bd \end{align}||
Pour valider ta compréhension à propos des vecteurs de façon interactive, consulte la MiniRécup suivante :
