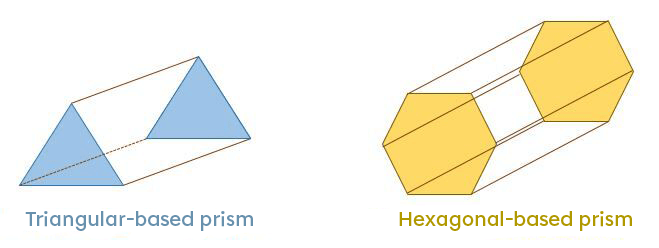
The net of a prism consists of each of its faces drawn on a sheet of paper, on the same plane. When the net is cut out, the edges of the net can simply be folded to form the solid.
The net of a right prism is a 2-dimensional representation of the prism with two isometric bases and its rectangular lateral faces, which may not necessarily be isometric.
In this section, only the net of the cube and right prisms are presented.
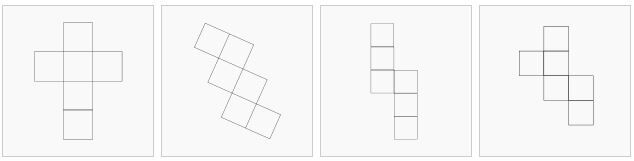
Since the cube is the only prism with all identical faces, it is worth illustrating its net, since it differs from other prisms.
Note that each face is represented on the net of a solid. Here we can see how the cube is expanded to create its net.
The cube’s net can be constructed in different ways by drawing each of its six square faces on a sheet of paper. However, these squares must be properly connected to each other.
Here are some of the different possible nets of a cube.
It is easiest to construct the net of a prism starting with its bases because the lateral faces must be rectangles. By definition, a prism has two isometric and parallel bases.
To represent a prism in 3 dimensions, you can generally follow these steps:
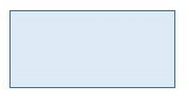
Step 1: Draw the first base using the necessary construction tools. See the following concept sheet if needed: Constructing Polygons.
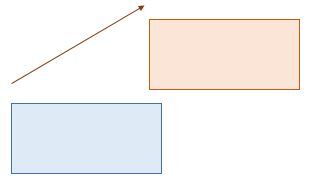
Step 2: Draw the image figure that results from a translation of the first base.
Step 3: Connect the two bases by drawing segments that join the corresponding vertices.

With this procedure, all you need to do is take your time to draw the first base as accurately as possible. After that, the translation is relatively straightforward and it's easy to connect the corresponding vertices.