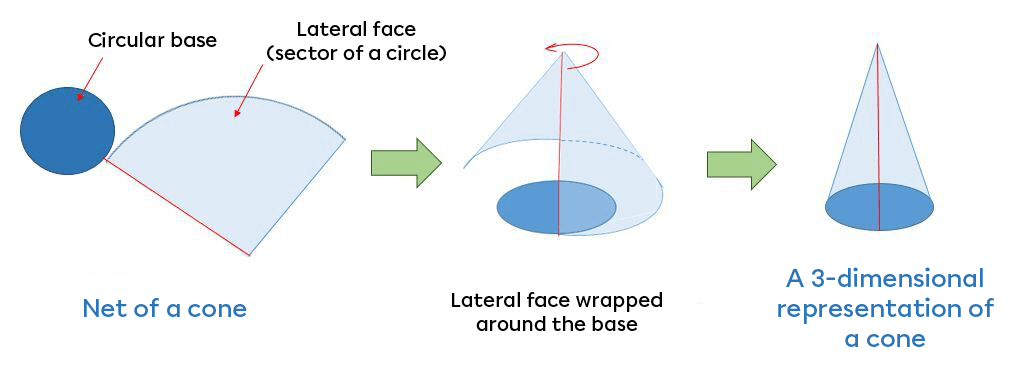
The net of a cone is produced when its two faces are drawn flat on a sheet of paper, on the same plane.
The net of a cone is a 2-dimensional representation where the base is a circle and the lateral face is a sector of a circle.
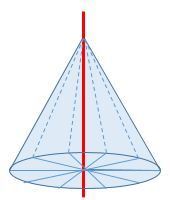
When the vertex (apex) of the cone is directly aligned above the centre of the base, it is called a right cone.
A cone is classified as a curved solid with a single base (a circle) and one lateral face (a sector of a circle).
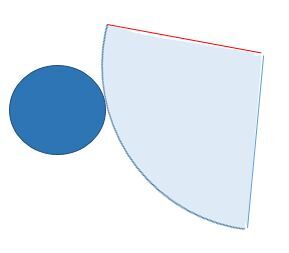
In the previous example, the lateral face (sector of a circle) was connected to the circle by its end point, which made it easier to visualize how it winds around the base. However, the net of the cone can be represented in many ways, as long as the curved portion of the side of the cone touches the circle at any one point.
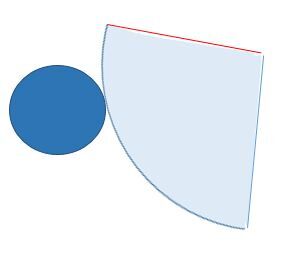
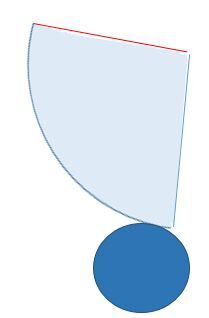
For the lateral face to wrap properly around the circular base, the arc of the sector of a circle must be the same length as the circumference of the circle that serves as the base.
The measure of the sector’s central angle is directly linked to the circumference of the base: as the measure of the angle increases, so does the measure of the circumference of the base.
What is the measure of the central angle of the sector that represents the lateral face of a cone with an apothem (slant height) of 5 cm and a base radius of 3 cm?
Using the properties of circular arcs, we can infer the following equation:||\begin{align}\dfrac{\text{Central angle}}{360^\circ}&=\dfrac{\text{Length of the arc}}{\text{Circumference}}\\\\\dfrac{\text{Central angle}}{360^\circ}&=\dfrac{\text{Circumference of the base}}{\begin{gathered}\text{Circumference of the circle}\\\text{defined by the sector}\end{gathered}}\\\\\dfrac{\text{Central angle}}{360^\circ}&=\dfrac{2\pi\times3}{2\pi\times 5}\\\\\dfrac{\text{Central angle}}{360^\circ} &=\dfrac{\cancel{2\pi}\times3}{\cancel{2\pi}\times 5}\\\\\dfrac{\text{Central angle}}{360^\circ} &=\dfrac{3}{5}\\\\\text{Central angle}&=\dfrac{3\times360^\circ}{5}\\\\\text{Central angle}&=216^\circ\end{align}||
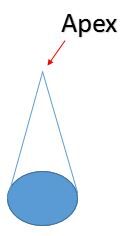
A cone can be constructed by drawing the circular base and then connecting its end points to its apex.
Step 1: Represent the base of the cone as an oval.

Step 2: Connect the right end point of a diameter line of the circle to the vertex of the cone (apex).
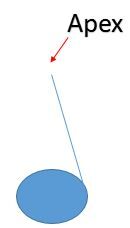
Step 3: Connect the left end point of the same diameter line to the apex.
A cone can also be made by rotating a triangle about an axis.
Step 1: The starting triangle must be placed at a right angle with respect to the axis of rotation to form a right cone.
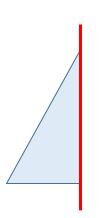
Step 2: Rotating this triangle by |90^\circ| forms a quarter cone.
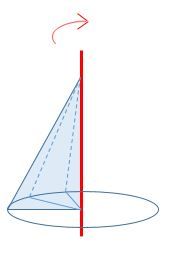
Step 3: Rotating this triangle by |180^\circ| forms a half-cone.
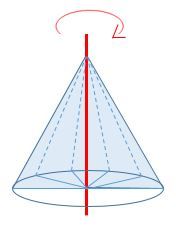
Step 4: Rotating this triangle by |360^\circ| forms a complete cone.