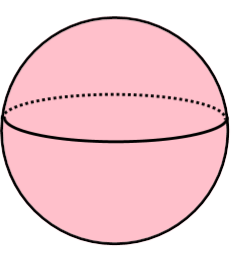
Because their surfaces consist entirely of curves, spheres are geometric shapes that cannot be perfectly broken down into two dimensions (2-D).
A sphere is the surface (area) consisting of the cluster/locus of points located at the same distance from a point, called the “centre.”
On the other hand, the interior of a sphere refers to the space (volume) occupied by the sphere.
Even so, we can try to approximate its net based on the formula for its surface area.
As explained above, it is impossible to break down a sphere perfectly into a 2-D form. However, we can associate its net with those of several circles.
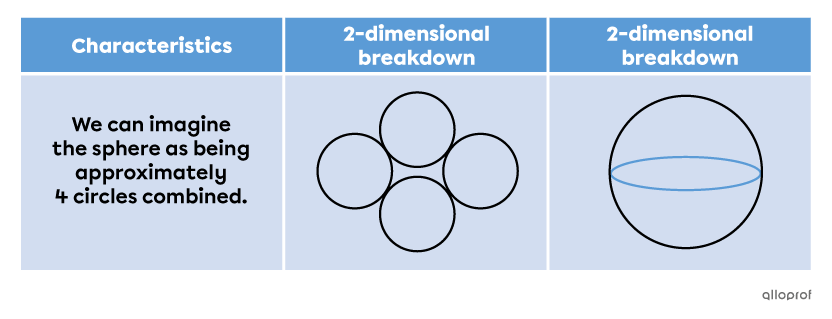
This estimation can be understood by comparing the formulas for the area of a circle and a sphere.
||\begin{align} Area_{circle}&=\pi r^{2}\\
Area_{sphere}&=4\pi r^{2}\end{align}||
Notice that:
||\begin{align}Area_{sphere}&=4\times(\pi r^{2})\\
&=4\times Area_{circle}\end{align}||
which explains the approximation of the sphere's net into 4 circles.
To do this, we base ourselves on its circular appearance, then add a few details to emphasize its three-dimensional aspect.
1. Draw a circle using a compass.

2. Add depth by drawing a dotted half-ellipse curving towards the back of the sphere.
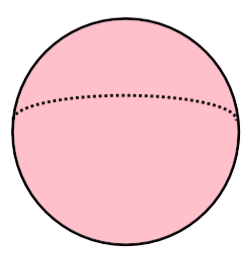
3. Finish the depth effect by drawing the same half-ellipse with a solid line curving forward.