The net of a pyramid consists of each of its faces drawn flat on a sheet of paper, on the same plane. Once cut out, the edges of the net can be folded to form the pyramid.
The net of a pyramid is a 2-dimensional representation of a pyramid, consisting of its base along with all of the lateral faces, which are necessarily triangles.
As a general rule, we aim to work with right pyramids. In other words, we try to ensure that the peak of the pyramid (the apex) lies above the centre of the base.
It is easy to recognize the net of a pyramid: its lateral faces are always triangles. Moreover, the pyramid has only one base, which can be in the shape of any polygon. In particular, if the base of the pyramid is an equilateral triangle, the pyramid is called a tetrahedron.
In the illustration below, we can see the pyramid in its initial state and watch its net be constructed in a few steps.
Once the above net has been mastered, it is easier to understand the nets of pyramids with non-square bases.
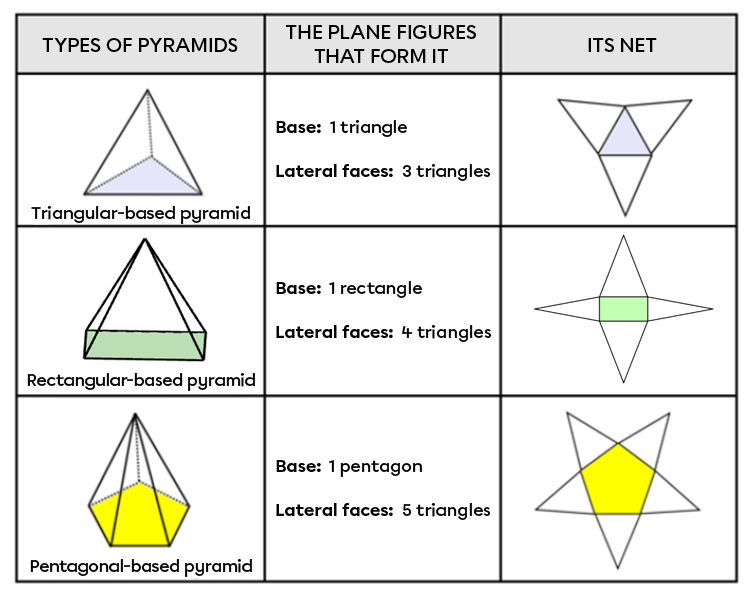
To represent a pyramid in 3 dimensions, start by constructing its base. Next, form a triangle from one of the base's sides. Lastly, join each vertex of the base to the apex of the pyramid.
Step 1: Draw the base using the necessary construction tools. See the following concept sheet if needed: Constructing Polygons.
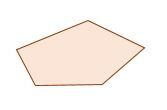
Step 2: Construct a first triangle from two consecutive vertices of the base.
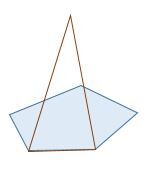
Step 3: Each vertex of the base is connected to the apex formed by the first triangle.
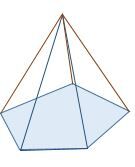
Simply change the base to create a different type of pyramid.
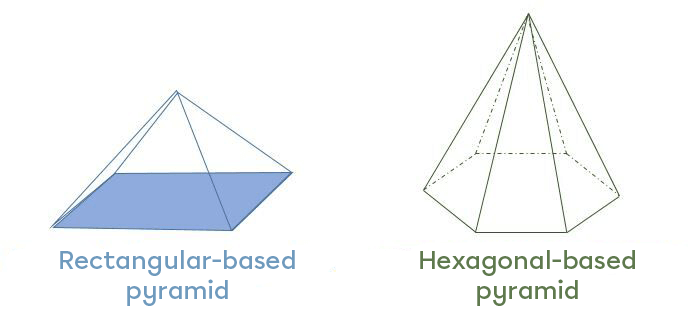
In the rectangular-based pyramid, the rectangle looks more like a parallelogram. This distortion is caused by the perspective effect of the 3-dimensional drawing.