Sometimes, a figure needs to be made larger or smaller. When the final figure has the same proportions as the initial one, the transformation is called a dilation (also known as uniform scaling or homothety).
A dilation, denoted |h_{(O,k)},| is a geometric transformation that makes it possible to enlarge or reduce a figure according to a scale factor |k| and a centre of dilation |O.|
A dilation proportionally increases or decreases the side measurements of a figure.
The expressions "ratio of similarity" and "scale factor" represent the same value and are denoted by the variable |k.|
However, the ratio of similarity uses the measurements of corresponding sides and the centre of dilation. Nevertheless, in both cases, the final value obtained will be the same.
To learn more about this subject, see the concept sheet about similarity ratio.
The scale factor determines the size of the figure image obtained by dilation. It can also impact the figure’s orientation.
When the scale factor is positive, the vertices of the initial figure and the image are on the same side of the centre of dilation.
Example of enlargement |(k>1)|
The rectangle |A'B'C'D'| was obtained by dilation through the centre |O| of the rectangle |ABCD| using a scale factor of |k = 2.|
Example of reduction |(0<k<1)|
The rectangle |E'F'G'H'| was obtained by dilation through the centre |O| of the rectangle |EFGH| using a scale factor of |k = 0.5.|
When the scale factor is negative, the vertices of the initial figure and the image are located on opposite sides of the centre of dilation.
Example of enlargement |(k<-1)|
The quadrilateral |A'B'C'D'| was obtained by dilating the quadrilateral |ABCD| using a scale factor of |k = -2.|
Example of reduction |(-1<k<0)|
The trapezoid |E'F'G'H'| was obtained by dilating the trapezoid |EFGH| using a scale factor of |k = -0.75.|
By keeping these relationships in mind, it becomes easier to verify the resulting image when constructing a dilation.
To construct a dilation, use the centre of dilation and the scale ratio |(k).| To do this, use a ruler and a pencil.
-
Draw a straight line connecting each of the vertices to the centre of dilation. To make the line easier to follow, make sure the line extends beyond the centre of dilation and the vertex.
-
Using a ruler, measure the distance between each vertex of the figure and the centre of dilation.
-
Multiply each of the distances by the dilation ratio |k.|
-
On the correct side of the centre of dilation, mark the distances obtained on each line and clearly identify each vertex of the image using the “ ' “ symbol.
-
Connect the image vertices to construct the figure.
In the following interactive animation, it’s possible to move the points |O| (the centre of dilation), |A|, |B|, and |C| (vertices of the initial triangle) and modify the value of the scale factor. By modifying the elements during different points of the animation, their impact on the image can be fully understood.
While modifying the scale factor, notice that a scale factor between |0| and |1| decreases the size of the figure, and a scale factor greater than |1| increases its size.
When the scale factor is negative, it is important to extend the lines connecting the centre of dilation to the vertices beyond both sides of the centre.
When the calculations are done, the distance obtained is negative. Geometrically speaking, a negative distance means that it is necessary to measure towards the opposite side from the centre of dilation.
To find the centre of dilation, use the information provided by the original figure and the image.
-
Draw a line passing through |A| and |A'|.
-
Draw a line passing through |B| and |B'|.
-
Draw the centre of dilation at the point of intersection of the two lines.
A minimum of two lines is necessary to find the centre of dilation. If a third and a fourth line are drawn, they will all pass through the same point of intersection found using the first two lines.
In the following animation, the vertices of the initial figure can be moved. Move the image figure horizontally and vertically to change the value of the scale factor.
Sometimes, the value of the scale factor |k| is given and the dilation needs to be drawn. In other cases, it is the opposite: the dilation is already drawn and the value of the scale factor needs to be found.
It is possible to determine the scale factor using the centre of dilation and at least two points, one of which is the image of the other.
||\begin{align}
k\ &=\ \displaystyle \frac{\text{Distance between the centre of dilation and the vertex of an image}}{\text{Distance between the centre of dilation and an initial vertex}}\\
&=\ \frac{m \ \overline{OA'}}{m \ \overline{OA}}
= \frac{m \ \overline{OB'}}{m \ \overline{OB}}
= \frac{m \ \overline{OC'}}{m \ \overline{OC}}
=\ ... \end{align}||
with
||\begin{align}
O &=&& \text{centre of dilation} \\
A,B,C,... &=&& \text{Vertices of the original figure}\\
A', B', C', ... & = && \text{Vertices of the image}
\end{align}||
The following examples illustrate the steps for determining the scale factor of a dilation.
-
If necessary, find the centre of dilation
-
Measure a line to a vertex of your choice in the image
-
Measure a line to the corresponding vertex of the initial figure
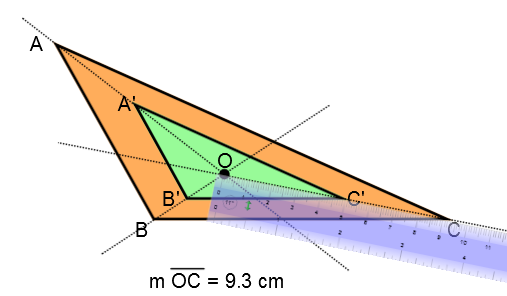
-
Calculate the scale factor |k| according to the formula
|k = \displaystyle \frac{\text{m} \overline{OC'}}{\text{m} \overline {OC}} = \displaystyle \frac{5}{9.3} \approx 0.54| -
Determine the sign of the scale factor |k.|
In this example, the points |C| and |C'| are on the same side of the centre of dilation. So, the scale factor is positive.
Thus, |k \approx 0.54.|