The ratios of similarity, area, and volume indicate either an enlargement or a reduction of the image figure with respect to the initial figure.
If the image figure is larger then the initial figure, then:||k=\dfrac{\color{#333fb1}{\text{Image Figure}}}{\color{#3a9a38}{\text{Initial Figure}}}=\dfrac{\color{#333fb1}{\text{Large Figure}}}{\color{#3a9a38}{\text{Small Figure}}}||where |k>1|
In this case, |k| is an enlargement ratio.
If the image figure is smaller then the initial figure, then:||k=\dfrac{\color{#333fb1}{\text{Image Figure}}}{\color{#3a9a38}{\text{Initial Figure}}}=\dfrac{\color{#333fb1}{\text{Small Figure}}}{\color{#3a9a38}{\text{Large Figure}}}||where |0<k<1|
In this case, |k| is a reduction ratio.
Similarity, area, and volume ratios are only valid when comparing corresponding lengths, areas, or volumes. For example, the height of one pyramid with the apothem of another pyramid cannot be compared, because they are not corresponding segments.
The similarity ratio (or scale factor) |\boldsymbol{(k)}| is the relationship between the corresponding lengths (i.e., sides, perimeters, radii, circumference, etc.) of two similar figures.
||k=\dfrac{\text{Length on the image figure}}{\text{Corresponding length on the initial figure}}||or||k=\dfrac{\text{Length on the image solid}}{\text{Corresponding length on the initial solid}}||
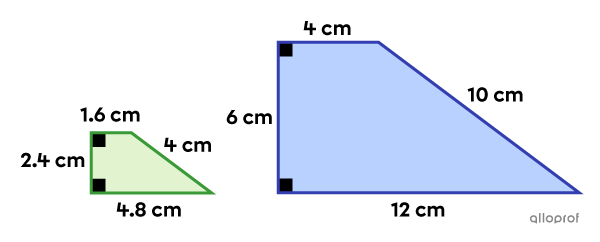
Find the similarity ratio |(k)| between the following similar trapezoids, if the blue trapezoid is the image figure and the green trapezoid the initial figure.
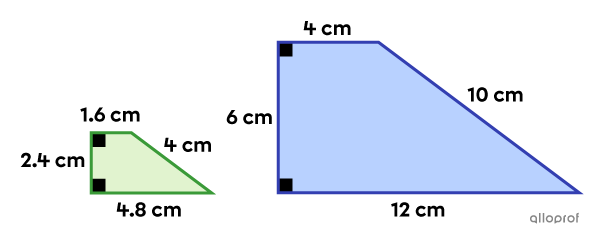
To calculate the similarity ratio (scale factor), we can use the large bases.
||\begin{align}k&=\dfrac{\color{#333fb1}{\text{Large base of the image trapezoid}}}{\color{#3a9a38}{\text{Large base of the initial trapezoid}}}\\k&=\dfrac{\color{#333fb1}{12\ \text{cm}}} {\color{#3a9a38}{4.8\ \text{cm}}}\\k&=\dfrac{5}{2}\end{align}||Applying the same reasoning to all the pairs of corresponding lengths, the same |k| value is always obtained.
Small Bases||\begin{align}k&=\dfrac{\color{#333fb1}{4\ \text{cm}}}{\color{#3a9a38}{1.6\ \text{cm}}}\\ k&=\dfrac{5}{2}\end{align}||Heights||\begin{align}k&=\dfrac{\color{#333fb1}{6\ \text{cm}}}{\color{#3a9a38}{2.4\ \text{cm}}}\\ k&=\dfrac{5}{2}\end{align}||
Oblique Sides||\begin{align}k&=\dfrac{\color{#333fb1}{10\ \text{cm}}}{\color{#3a9a38}{4\ \text{cm}}}\\ k&=\dfrac{5}{2}\end{align}||Perimeters||\begin{align}k&=\dfrac{\color{#333fb1}{12}+\color{#333fb1}{6}+\color{#333fb1}{4}+\color{#333fb1}{10}}{\color{#3a9a38}{4.8}+\color{#3a9a38}{2.4}+\color{#3a9a38}{1.6}+\color{#3a9a38}{4}}\\
k&=\dfrac{\color{#333fb1}{32\ \text{cm}}}{\color{#3a9a38}{12.8\ \text{cm}}}=\dfrac{5}{2}\end{align}||
Answer: The similarity ratio is |k=\dfrac{5}{2}.| Since |k>1,| it’s an enlargement ratio.
Note: All the ratios are equivalent. Otherwise, the 2 figures would not be similar. Also, if the blue trapezoid was the initial figure and the green trapezoid the image figure, then |k| would have been a reduction ratio with a value of |\dfrac{2}{5}.|
Find the height of the blue prism, if it is similar to the green prism.
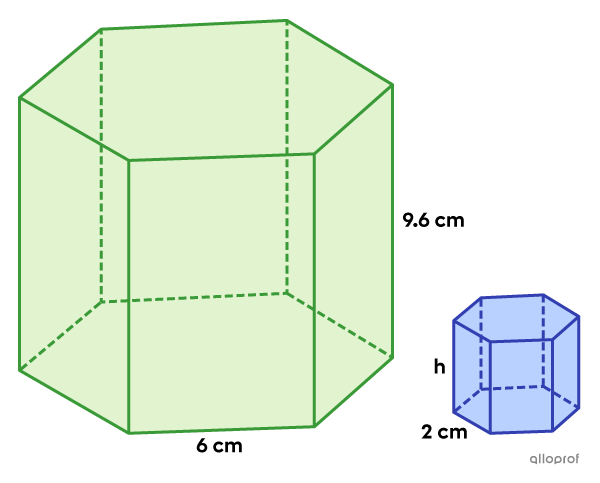
The blue prism can be defined as the image figure.
-
Calculate the scale factor |\boldsymbol{k}|
Since the measure of the edges of the base is known, the value of |k| is supplied by the following ratio. ||\begin{align}k&={\dfrac{\color{#333fb1}{\text{Image prism’s edge of base}}}{\color{#3a9a38}{\text{Initial prism’s edge of base}}}}\\k&=\dfrac{\color{#333fb1}{2\ \text{cm}}}{\color{#3a9a38}{6\ \text{cm}}}\\k&=\dfrac{1}{3}\end{align}||
-
Calculate the missing measure
The missing measure can be calculated using the method for balancing equations. ||\begin{align}k&={\dfrac{\color{#333fb1}{\text{Height of image figure}}}{\color{#3a9a38}{\text{Height of initial figure}}}}\\\dfrac{1}{3}&=\dfrac{\color{#333fb1}{h}}{\color{#3a9a38}{9.6}}\\\dfrac{1}{3}\color{#ec0000}{\times9.6}\ &=\dfrac{h}{9.6}\color{#ec0000}{\times 9.6}\\3.2\ \text{cm}&=h\end{align}||Answer: The measure of the height of the blue prism is |3.2\ \text{cm}.|
The ratio of areas |\boldsymbol{(k^2)}| is a ratio of the corresponding surfaces (areas of plane figures, bases of prisms, side faces of pyramids, etc.) of two similar figures.
||k^2=\dfrac{\text{Area of the image figure}}{\text{Area of the initial figure}}||or||k^2=\dfrac{\text{Face on the image solid}}{\text{Corresponding face on the initial solid}}||
Find the ratio of the areas |(k^2)| between the following similar trapezoids, if the blue trapezoid is the image figure and the green trapezoid the initial figure.
-
Calculate the areas
To calculate the ratio |k^2| between the 2 figures, first calculate the areas of the trapezoids.
Area of the Initial Figure||\begin{align}A_\text{initial}&=\dfrac{(B+b)\times h}{2}\\A_\text{initial}&=\dfrac{(4.8+1.6)\times2.4}{2}\\A_\text{initial}&=7.68\ \text{cm}^{2}\end{align}||
Area of the Image Figure||\begin{align}A_\text{image}&=\dfrac{(B+b)\times h}{2}\\A_\text{image}&=\dfrac{(12+4)\times6}{2}\\A_\text{image}&=48\ \text{cm}^{2}\end{align}||
-
Calculate the ratio of areas
||\begin{align}k^2&=\dfrac{\color{#333fb1}{\text{Area of the Image Trapezoid}}}{\color{#3a9a38}{\text{Area of the Initial Trapezoid}}}\\k^2&=\dfrac{\color{#333fb1}{48\ \text{cm}^2}}{\color{#3a9a38}{7.68\ \text{cm}^2}}\\k^2&=\dfrac{25}{4}\end{align}||Answer: The ratio of areas |(k^2)| is |\dfrac{25}{4}.|
Find the lateral area of the blue prism if it is similar to the green prism.
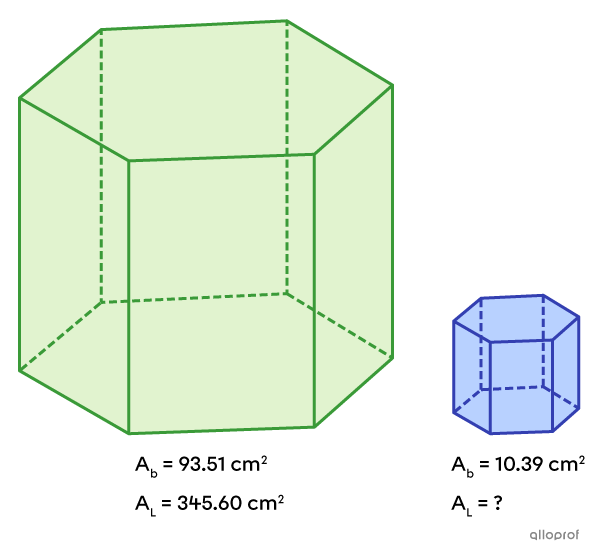
We can define the blue prism as the image figure.
-
Calculate the ratio |\boldsymbol{k^2}|
Since we know the measurements of the areas of the bases, the value of |k^2| can be calculated, as follows.||\begin{align}k^2&={\dfrac{\color{#333fb1}{\text{Area of the Base of the Image Prism}}}{\color{#3a9a38}{\text{Area of the Base of the Initial Prism}}}}\\k^2&=\dfrac{\color{#333fb1}{10.39\ \text{cm}^2}}{\color{#3a9a38}{93.51\ \text{cm}^2}}\\k^2&=\dfrac{1}{9}\end{align}||
-
Calculate the Missing Measure
||\begin{align}k^2&={\dfrac{\color{#333fb1}{\text{Lateral Area of the Image Prism}}}{\color{#3a9a38}{\text{Lateral Area of the Initial Prism}}}}\\\dfrac{1}{9}&=\dfrac{\color{#333fb1}{A_L}}{\color{#3a9a38}{345.60}}\\\dfrac{1}{9}\color{#ec0000}{\times345.60}&=\dfrac{A_L}{345.60}\color{#ec0000}{\times345.60}\\38.4\ \text{cm}^2&=A_L\end{align}||Answer: The lateral area of the blue prism is |38.4\ \text{cm}^2.|
The ratio of volumes |\boldsymbol{(k^3)}| is a ratio of the volumes of two similar solids.
||k^3=\dfrac{\text{Volume of the image solid}}{\text{Volume of the initial solid}}||
Find the ratio of volumes |(k^3)| between the following similar trapezoidal-based prisms, if the blue prism is the image solid and the green prism the initial solid.
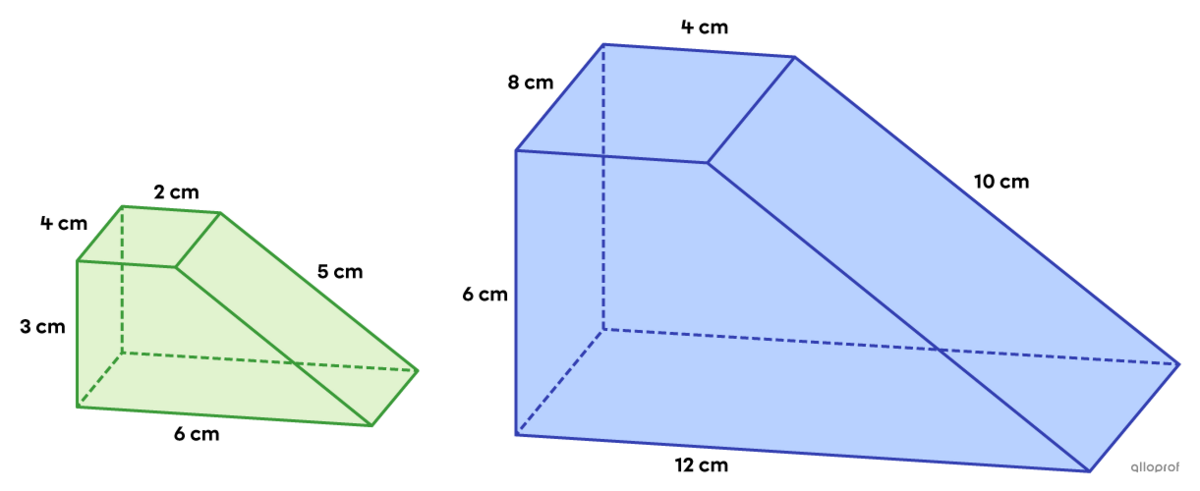
-
Calculate the volumes
To calculate the ratio |k^3| between the two solids, first calculate the volumes of the prisms.
Calculate the volume of the initial solid||\begin{align}V_\text{initial}&=A_b\times h_{\text{prism}}\\V_\text{initial}&=\dfrac{(B+b)\times h_{\text{trapezoid}}}{2}\times h_{\text{prism}}\\V_\text{initial}&=\dfrac{(6+2)\times 3}{2}\times 4\\V_\text{initial}&=48\ \text{cm}^3\end{align}||
Calculate the volume of the image solid||\begin{align}V_\text{image}&=A_b\times h_{\text{prism}}\\V_\text{image}&=\dfrac{(B+b)\times h_{\text{trapezoid}}}{2}\times h_{\text{prism}}\\V_\text{image}&=\dfrac{(12+4)\times 6}{2}\times 8\\V_\text{image}&=384\ \text{cm}^3\end{align}||
-
Calculate the ratio of volumes
||\begin{align}k^3&=\dfrac{\color{#333fb1}{\text{Volume of the Image Prism}}}{\color{#3a9a38}{\text{Volume of the Initial Prism}}}\\k^3&=\dfrac{\color{#333fb1}{384\ \text{cm}^3}}{\color{#3a9a38}{48\ \text{cm}^3}}\\k^3&=8\end{align}||Answer: The ratio of volumes |(k^3)| is |8.|
Find the volume of the blue prism if it is similar to the green prism by a ratio of |k^3=\dfrac{1}{27}.|

Since |k^3| is between |0| and |1,| it is a reduction ratio. Therefore, the image figure is the blue prism. The definition of the ratio of volumes |k^3,| results in the following.||\begin{align}k^3&=\dfrac{\color{#333fb1}{\text{Volume of the Image Prism}}}{\color{#3a9a38}{\text{Volume of the Initial Prism}}}\\\dfrac{1}{27}&=\dfrac{\color{#333fb1}{V}}{\color{#3a9a38}{899.1}}\\\dfrac{1}{27}\color{#ec0000}{\times899.1}&=\dfrac{V}{899.1}\color{#ec0000}{\times899.1}\\33.3\ \text{cm}^3&=V\end{align}||Answer: The volume of the blue prism is |33.3\ \text{cm}^3.|
The following interactive tool illustrates what happens to lengths, areas, and volumes when changing the value of |k.|
-
How many times does the green length fit into the blue length?
-
How many times does the green square fit into the blue square?
-
How many times does the green cube fit into the blue cube?
|\boldsymbol{k=2}|
-
The green length fits |2| times inside the blue length. In other words, the blue length is |2| times longer than the green length.
-
The green square fits |4| times inside the blue square. In other words, the area of the blue square is |4| times larger than the green square’s.
-
The green cube fits |8| times into the blue cube. In other words, the volume of the blue cube is |8| times larger than the green cube’s.
|\boldsymbol{k=3}|
-
The green length fits |3| times inside the blue length. In other words, the blue length is |3| times longer than the green length.
-
The green square fits |9| times into the blue square. In other words, the area of the blue square is |9| times larger than the green square’s.
-
The green cube fits |27| times into the blue cube. In other words, the volume of the blue cube is |27| times larger than the green cube’s.
When the value of one of the 3 ratios is known, it is possible to find the value of the other 2 using the properties of exponents and roots. The following diagram summarizes the operations necessary to change from one ratio to the other.
To correctly use the diagram, it is essential to follow the direction of the arrows. For example, to go from |k^3| to |k^2,| follow the path |k^3\rightarrow k\rightarrow k^2.|

Here is how to proceed when looking for missing measurements using |k,| |k^2| and |k^3.|
-
Identify the ratio required to find the missing measure
-
Calculate the ratio required to find the missing measure using the relationships between the ratios.
-
Calculate the missing measure.
Find the area of the base of the blue cone, knowing it is similar to the green cone.
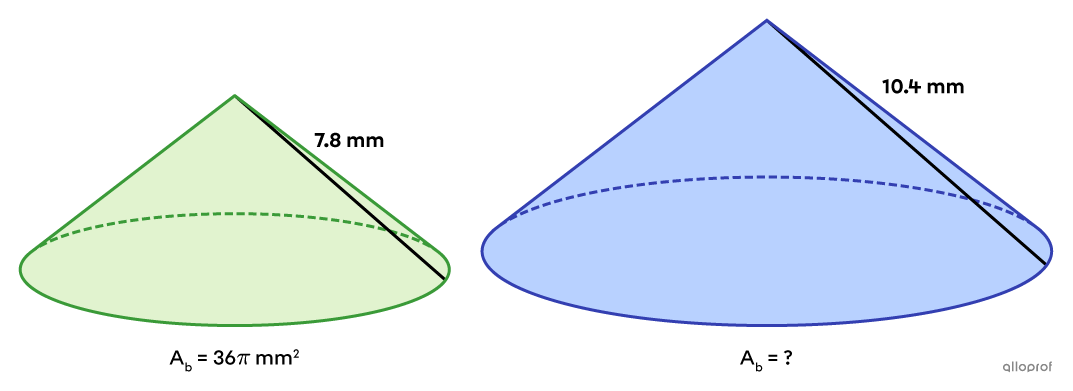
-
Identify the ratio needed to find the missing measure.
Since we are looking for the measure of the area of a base, we need to know the value of |k^2,| which is the ratio of the areas. For the moment, we can only find the value of |k,| because we know the measure of the apothems.
-
Calculate the ratio to find the missing measure using the relationship between the ratios.
We can define the image figure as the blue cone. So, the value of |k| is supplied by the following ratio.||\begin{align}k&={\dfrac{\color{#333fb1}{\text{Apothem of the Image
Cone}}}{\color{#3a9a38}{\text{Apothem of the Initial Cone}}}}\\k&=\dfrac{\color{#333fb1}{10.4\ \text{mm}}}{\color{#3a9a38}{7.8\ \text{mm}}}\\k&=\dfrac{4}{3}\end{align}||Next, calculate the value of |k^2.|||\begin{align}k^2&=\color{#EC0000}{(\color{black}{k})^2}\\k^2&=\left(\dfrac{4}{3}\right)^2\\k^2&=\dfrac{4^2}{3^2}\\k^2&=\dfrac{16}{9}\end{align}||
-
Calculate the missing measure.
||\begin{align}k^2&=\dfrac{\color{#333fb1}{\text{Area of the Base of the Image Cone}}}{\color{#3a9a38}{\text{Area of the Base of the Initial Cone}}}\\\dfrac{16}{9}&=\dfrac{\color{#333fb1}{A_b}}{\color{#3a9a38}{36\pi}}\\\dfrac{16}{9}\color{#ec0000}{\times36\pi}&=\dfrac{A_b}{36\pi}\color{#ec0000}{\times36\pi}\\64\pi\ \text{mm}^2&=A_b\end{align}||Answer: The area of the base of the blue cone is |64\pi\ \text{mm}^2.|
Find the volume of the blue cylinder knowing it is similar to the green cylinder.
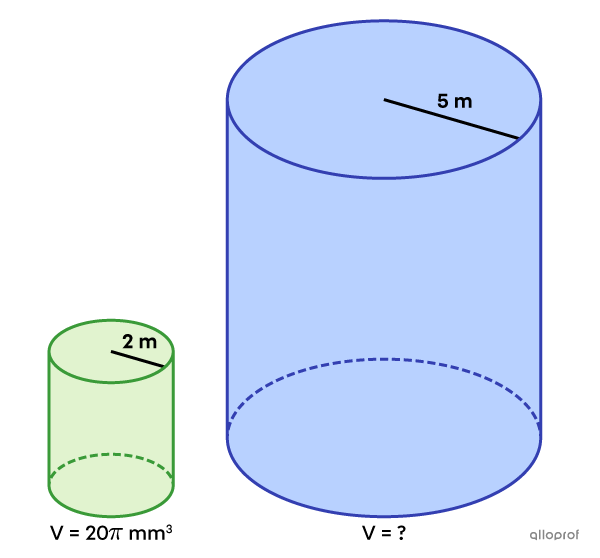
-
Identify the ratio needed to find the missing measure.
Since we are looking for the volume, we need to know the value of |k^3.| For now, we can only find the value of |k,| because we know the measurements of the radii.
-
Calculate the ratio needed to find the missing measure using the relationship between the ratios.
We can define the image figure as the blue cylinder. Therefore, the value of |k| is supplied by the following ratio.||\begin{align}k&={\dfrac{\color{#333fb1}{\text{Radius of the Image Cylinder}}}{\color{#3a9a38}{\text{Radius of the Initial Cylinder}}}}\\k&=\dfrac{\color{#333fb1}{5\ \text{m}}}{\color{#3a9a38}{2\ \text{m}}}\\k&=\dfrac{5}{2}\end{align}||Next, calculate the value of |k^3.|||\begin{align}k^3&=\color{#EC0000}{(\color{black}{k})^3}\\k^3&=\left(\dfrac{5}{2}\right)^3\\k^3&=\dfrac{5^3}{2^3}\\k^3&=\dfrac{125}{8}\end{align}||
-
Calculate the missing measure.
||\begin{align}k^3&=\dfrac{\color{#333fb1}{\text{Volume of the Image Cylinder}}}{\color{#3a9a38}{\text{Volume of the Initial Cylinder}}}\\\dfrac{125}{8}&=\dfrac{\color{#333fb1}{V}}{\color{#3a9a38}{20\pi}}\\\dfrac{125}{8}\color{#ec0000}{\times20\pi}&=\dfrac{V}{20\pi}\color{#ec0000}{\times20\pi}\\312.5\pi\ \text{m}^3&=V\end{align}||Answer: The volume of the blue cylinder is |312.5\pi\ \text{m}^3.|
Find the lateral area of the blue pyramid if it is similar to the green pyramid.
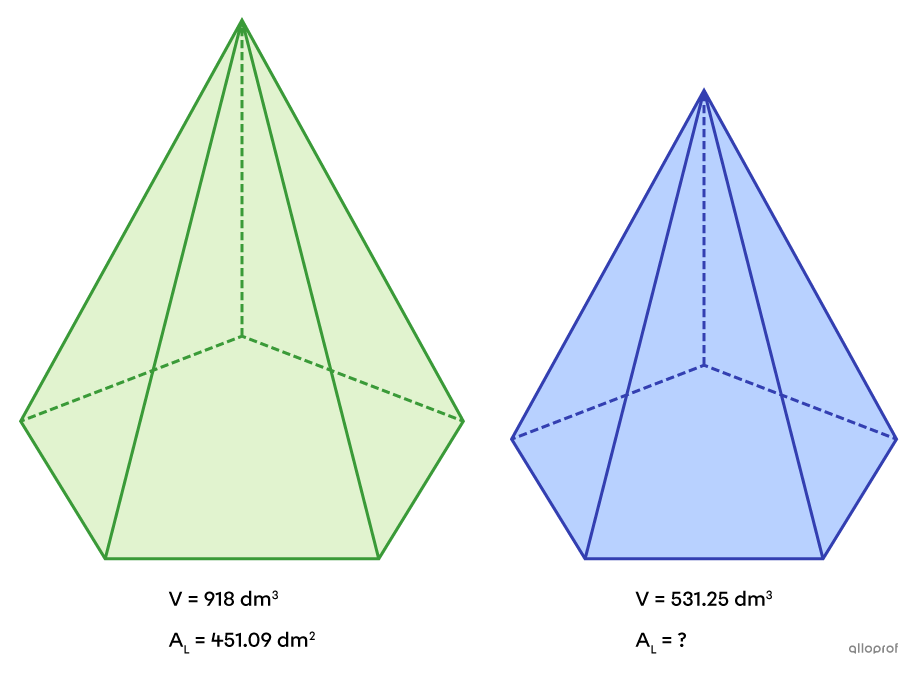
-
Identify the ratio needed to find the missing measure.
Since we are looking for an area, we need to know the value of |k^2.| For now, we can only find the value of |k^3,| because we know the volumes.
-
Calculate the ratio needed to find the missing measure using the relationship between the ratios.
We can define the blue figure as the image figure. Therefore, the value of |k^3| is supplied by the following ratio.||\begin{align}k^3&={\dfrac{\color{#333fb1}{\text{Volume of the Image Pyramid}}}{\color{#3a9a38}{\text{Volume of the Initial Pyramid}}}}\\k^3&=\dfrac{\color{#333fb1}{531.25\ \text{dm}^3}}{\color{#3a9a38}{918\ \text{dm}^3}}\\k^3&=\dfrac{125}{216}\end{align}||Next, we can calculate the value of |k^2| using the following.||k^3\rightarrow k\rightarrow k^2||
||\begin{align}k&=\color{#ec0000}{\sqrt[3]{\color{black}{k^3}}}\\k&=\sqrt[3]{\dfrac{125}{216}}\\k&=\dfrac{\sqrt[3]{125}}{\sqrt[3]{216}}\\k&=\dfrac{5}{6}\end{align}||
||\begin{align}k^2&=\color{#ec0000}{(\color{black}{k})^2}\\k^2&=\left(\dfrac{5}{6}\right)^2\\k^2&=\dfrac{5^2}{6^2}\\k^2&=\dfrac{25}{36}\end{align}||
-
Calculate the missing measure.
||\begin{align}k^2&=\dfrac{\color{#333fb1}{\text{Lateral Area of the Image Pyramid}}}{\color{#3a9a38}{\text{Lateral Area of the Initial Pyramid}}}\\\dfrac{25}{36}&=\dfrac{\color{#333fb1}{A_L}}{\color{#3a9a38}{451.09}}\\\dfrac{25}{36}\color{#ec0000}{\times451.09}&=\dfrac{A_L}{451.09}\color{#ec0000}{\times451.09}\\313.26\ \text{dm}^2&=A_L\end{align}||Answer: The lateral area of the blue pyramid is |313.26\ \text{dm}^2.|
The following similar solids are regular polyhedra called octahedra.
Find the measure of the edges and the volume of the orange octahedron and the light blue octahedron.
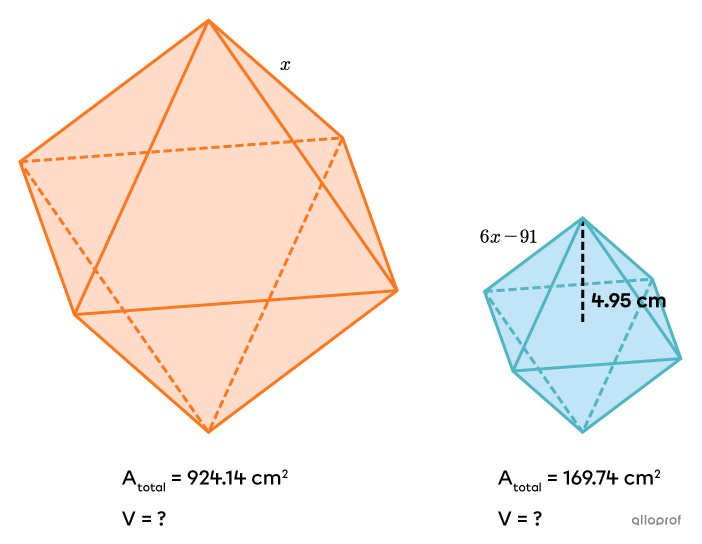
-
Identify the ratio needed to find the missing measure.
Since we are looking for the measure of the edges and the volume of the two octahedra, we need the values of |k| and |k^3.| For the moment, we can only find the value of |k^2,| because we know the total areas. -
Calculate the ratio |\boldsymbol{k}| using the relationship between the ratios.
We can define the image figure as one of the octahedra. We will choose the light blue octahedron as the image figure. Start by calculating the value of |k^2| which is supplied by the following ratio.
||\begin{align}k^2&=\dfrac{\color{#51b6c2}{\text{Total Area of the Image Octahedron}}}{\color{#fa7921}{\text{Total Area of the Initial Octahedron}}}\\k^2&=\dfrac{\color{#51b6c2}{169.74\ \text{cm}^2}}{\color{#fa7921}{924.14\ \text{cm}^2}}\\k^2&=\dfrac{9}{49}\end{align}||
Next, calculate the value of |k.|
||\begin{align}k&=\color{#ec0000}{\sqrt{\color{black}{k^2}}}\\k&=\sqrt{\dfrac{9}{49}}\\k&=\dfrac{\sqrt{9}}{\sqrt{49}}\\k&=\dfrac{3}{7}\end{align}||
The value of |k| is between |0| and |1.| It is perfectly normal because the image figure has been reduced. -
Calculate the measure of the edges
||\begin{align}k&=\dfrac{\color{#51b6c2}{\text{Edge of the Image Octahedron}}}{\color{#fa7921}{\text{Edge of the Initial Octahedron}}}\\\dfrac{3}{7}&=\dfrac{\color{#51b6c2}{6x-91}}{\color{#fa7921}{x}}\end{align}||
We use cross-multiplication to eliminate fractions, and then we isolate |x| by balancing the equation.
||\begin{align}3\color{#fa7921}x&=7(\color{#51b6c2}{6x-91})\\3x\color{#ec0000}{-42x}&=42x-637\color{#ec0000}{-42x}\\\color{#ec0000}{\dfrac{\color{black}{-39x}}{-39}}&=\color{#ec0000}{\dfrac{\color{black}{-637}}{-39}}\\x&=16.\overline{3}\ \text{cm}\end{align}||
Answer: The edges of the orange octahedron measure |16.\overline{3}\ \text{cm}.|
We can now calculate the measure of the edges of the pale blue octahedron by the substitution method.
||6\color{#fa7921}{x}-91=6(\color{#fa7921}{16.\overline{3}})-91=7\ \text{cm}||
Answer: Each edge of the pale blue octahedron measures |7\ \text{cm}.| -
Calculate the ratio |\boldsymbol{k^3}| using the relationship between the ratios
We already know the value of |k,| calculated in step 2. We can therefore directly calculate the value of |k^3.|
||\begin{align}k^3&=\color{#EC0000}{(\color{black}{k})^3}\\k^3&=\left(\dfrac{3}{7}\right)^3\\k^3&=\dfrac{3^3}{7^3}\\k^3&=\dfrac{27}{343}\end{align}|| -
Calculate the volumes
We know the measure of the edges and the half-height of the pale blue octahedron, suggesting we can calculate its volume. The octahedron is a decomposable solid formed by 2 congruent square pyramids. In other words, we can find the volume of an octahedron by calculating twice the volume of a pyramid.
||\begin{align}V&=2\times\dfrac{A_b\times h}{3}\\V&=2\times\dfrac{7^2\times4.95}{3}\\V&=161.7\ \text{cm}^3\end{align}||
Answer: The volume of the pale blue octahedron is |161.7\ \text{cm}^3.|
Lastly, we find the volume of the orange octahedron using the ratio |k^3| calculated in the previous step.
||\begin{align}k^3&=\dfrac{\color{#51b6c2}{\text{Volume of the Image Octahedron}}}{\color{#fa7921}{\text{Volume of the Initial Octahedron}}}\\\dfrac{27}{343}&=\dfrac{\color{#51b6c2}{161.7}}{\color{#fa7921}V}\\27\times V&=161.7\times 343\\\color{#ec0000}{\dfrac{\color{black}{27\times V}}{27}}&=\color{#ec0000}{\dfrac{\color{black}{161.7\times 343}}{27}}\\V&\approx2\ 054.19\ \text{cm}^3\end{align}||
Answer: The volume of the orange octahedron is |2\ 054.19\ \text{cm}^3.|
In the last example, the value of |k^3| used to calculate the volume of the orange octahedron is a reduction ratio |\left(0<\dfrac{27}{343}<1\right).| Since the orange octahedron is larger than the pale blue octahedron, we can also use the reciprocal of |\dfrac{27}{343}| to use an enlargement ratio. The approach would have been the following.
||\begin{align}\dfrac{1}{k^3}&=\dfrac{\color{#fa7921}{\text{Volume of the Initial Octahedron}}}{\color{#51b6c2}{\text{Volume of the Image Octahedron}}}\\\dfrac{343}{27}&=\dfrac{\color{#fa7921}V}{\color{#51b6c2}{161.7}}\\343\times161{,}7&=V\times27\\\color{#ec0000}{\dfrac{\color{black}{343\times161.7}}{27}}&=\color{#ec0000}{\dfrac{\color{black}{V\times27}}{27}}\\2\ 054.19\ \text{cm}^3&\approx V\end{align}||