The greatest common factor (GCF) of two or more numbers is the largest positive integer which simultaneously divides evenly into all the numbers.
When two or more numbers have a GCF equal to |1|, these numbers are said to be relatively prime or coprime.
There are several ways to determine the GCF of two or more numbers. This concept sheet will look at different methods to find the GCF as well as show the main kinds of problems that involve finding a GCF.
The methods presented below are used only to find the GCF. To learn how to find the LCM (least common multiple) and the GCF of two or more numbers at the same time, consult the following concept sheet.
To look for the greatest common factor, simply list the factors of the given numbers and identify the largest factor common to each. This method is good for smaller numbers.
-
List the factors of each number.
-
Identify the common factors.
-
Choose the largest factor.
Find the GCF of |30| and |45.|
-
List the factors of each number
They are:
|\begin{align}30&:\left\{1, 2, 3, 5, 6, 10, 15, 30\right\}\\
45&:\left\{1, 3, 5, 9, 15, 45\right\}\end{align}| -
Identify the common factors
|\begin{align}30&:\left\{\color{green}{1}, 2, \color{green}{3}, \color{green}{5}, 6, 10, \color{green}{15}, 30\right\}\\
45&:\left\{\color{green}{1}, \color{green}{3}, \color{green}{5}, 9, \color{green}{15}, 45\right\}\end{align}| -
Choose the largest factor
|\color{green}{15}| is the greatest common factor.
|GCF(30,45)=15|
Find the GCF of |15| and |26|.
-
List the factors of each number
They are:
|\begin{align}15&:\left\{1, 3, 5, 15\right\}\\
26&:\left\{1, 2, 13, 26\right\}\end{align}| -
Identify the common factors
|\begin{align}15&:\left\{\color{green}{1}, 3, 5, 15\right\}\\
26&:\left\{\color{green}{1}, 2, 13, 26\right\}\end{align}| -
Choose the largest factor
Note that |\color{green}{1}| is the greatest common factor.
|GCF(15,26)=1|
*Therefore, |15| and |26| are relatively prime or coprime.
Determine the GCF of |12|, |36|, and |60|.
-
List the factors of each number
They are:
|\begin{align}12&:\left\{1, 2, 3, 4, 6, 12\right\}\\
36&:\left\{1, 2, 3, 4, 6, 9, 12, 18, 36\right\}\\
60&:\left\{1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60\right\}\end{align}| -
Identify the common factors
|\begin{align}12&:\left\{\color{green}{1}, \color{green}{2}, \color{green}{3}, \color{green}{4}, \color{green}{6}, \color{green}{12}\right\}\\
36&:\left\{\color{green}{1}, \color{green}{2}, \color{green}{3}, \color{green}{4}, \color{green}{6}, 9, \color{green}{12}, 18, 36\right\}\\
60&:\left\{\color{green}{1}, \color{green}{2}, \color{green}{3}, \color{green}{4}, 5, \color{green}{6}, 10, \color{green}{12}, 15, 20, 30, 60\right\}\end{align}| -
Choose the largest factor>
|\color{green}{12}| is the greatest common factor.
|GCF(12,36,60)=12|
This method consists of simultaneously dividing the given numbers by prime factors. The GCF is obtained by multiplying these prime factors together at the end. This method is good for finding the GCF of two large numbers.
-
Draw a table, with the first column titled Prime Factors. The labels of the other columns are the numbers whose GCF must be found.
-
Simultaneously divide all the given numbers by the prime factors. Start with |2|, then |3|, |5|, |7|, and so on. Continue dividing until there are no more common factors.
-
Calculate the GCF by multiplying the prime factors listed in the first column.
Calculate the GCF of |36| and |90|.
-
Draw a table with the first column titled Prime factors. Label the other columns with the given numbers for which the GCF must be found.
-
Attempt to simultaneously divide all the given numbers by the prime factors. Continue dividing until there are no more common factors.
|
Prime Factors |
|36| |
|90| |
|---|---|---|
|
|\color{blue}{2}| |
|18| |
|45| |
|
|\color{blue}{3}| |
|6| |
|15| |
|
|\color{blue}{3}| |
|2| |
|5| |
-
Calculate the GCF by multiplying the prime factors listed in the first column.
|\begin{align}GCF(36,90)&=\color{blue}{2}\times \color{blue}{3}\times \color{blue}{3}\\ &=18\end{align}|
This versatile method consists of finding the prime factorization of all the numbers and then writing the GCF as the product of common factors.
-
Decompose each number into a product of its prime factors.
-
Identify the common factors.
-
Write the GCF as a product of these common factors.
The common factors must be common to all the numbers. For example, find the GCF of |60,| |84,| and |140.|
The prime factorization of these numbers is given below.
|\begin{align}60&=2\times 2\times 3\times 5\\
84&=2\times 2\times 3\times 7\\
140&=2\times 2\times 5\times 7\end{align}|
Here |3|, |5|, and |7| are not common factors since they only appear in two of the three prime factorizations of the numbers.
If a common factor occurs more than once, it must be included the same number of times in the GCF. Since the factor |2| is included in all numbers twice, it must be present twice in the GCF.
Therefore, |GCF(60,84,140)=2\times 2=4|.
Find the GCF of |24| and |84|.
-
Decompose each number into a product of its prime factors
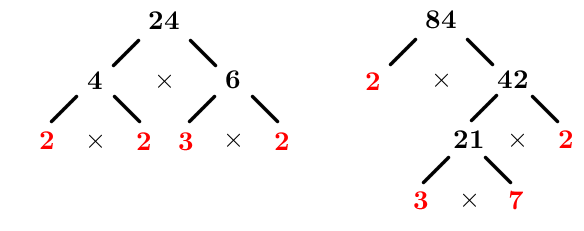
The factorizations are:
|\begin{align}24&=2\times 2\times 2\times 3 \\
84&=2\times 2\times 3\times 7 \end{align}|
-
Identify the common factors
|\begin{align}24&=\color{green}{2}\times \color{blue}{2}\times 2\times \color{purple}{3} \\
84&=\color{green}{2}\times \color{blue}{2}\times \color{purple}{3}\times 7 \end{align}|
-
Write the GCF as a product of these common factors
|\begin{align}GCF(24,84)&=\color{green}{2}\times\color{blue}{2}\times\color{purple}{3}\\ &=12\end{align}|
Determine the GCF of |40|, |60|, and |75|.
-
Decompose each number into a product of its prime factors
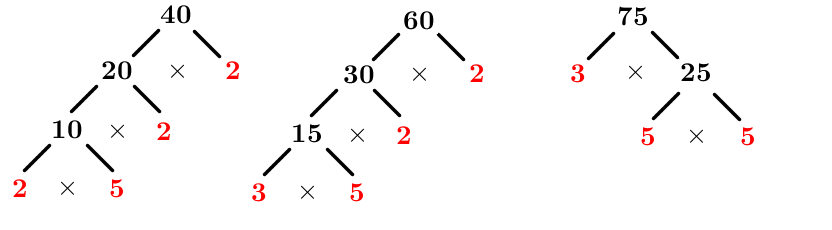
The factorizations are:
|\begin{align}40&=2\times 2\times 2\times 5 \\
60&=2\times 2\times 3\times 5\\
75&=3\times 5\times 5\end{align}|
-
Identify the common factors
|\begin{align}40&=2\times 2\times 2\times \color{green}{5} \\
60&=2\times 2\times 3\times \color{green}{5}\\
75&=3\times \color{green}{5}\times 5\end{align}|
-
Write the GCF as a product of these common factors
|GCF(40,60,75)=\color{green}{5}|
When solving word problems, finding the GCF may be necessary even if it has not been explicitly requested. Here are some situations where the GCF must be found in order to calculate the answer.
-
Find the largest number of equivalent groups that can be formed, given a certain number of elements.
-
Find the largest number of identical snacks that can be made, given different numbers of ingredients.
-
Find the largest number of individuals that can be placed into groups of equal size.
Here is how to solve these problems.
-
Read the problem carefully and decide if finding the GCF is necessary.
-
Identify the numbers whose GCF is required.
-
Calculate the GCF of these numbers.
-
Interpret the result.
There are two group reservations this evening in a restaurant: a group of |60| people and a group of |90| people. The plan is to seat as many individuals as possible at each table. Each table must seat groups of equal size. How many people should be seated at each table?
-
Read the problem carefully and decide if finding the GCF is necessary
The question asks to find the largest number of people that can be seated at each table, as long as the groups are the same size. This requires finding a GCF. -
Identify the numbers whose GCF is required
Find the greatest common factor of |60| and |90|. -
Calculate the GCF of these numbers
For this step, use any one of the methods above. Here is an example using the strategy that lists the factors one by one.
|\begin{align}60&:\left\{\color{green}{1}, \color{green}{2}, \color{green}{3}, 4, \color{green}{5}, \color{green}{6}, \color{green}{10}, 12, \color{green}{15}, 20, \underline{\color{green}{30}}, 60\right\}\\ 90&:\left\{\color{green}{1}, \color{green}{2}, \color{green}{3}, \color{green}{5}, \color{green}{6}, 9, \color{green}{10}, \color{green}{15}, 18, \underline{\color{green}{30}}, 45, 90\right\}\end{align}|
Therefore, the |GCF(60,90)=\color{green}{30}|. -
Interpret the result
Given a group of |60| and a group of |90|, the greatest number of people possible that can be seated at tables with an equal number of people is |30|.
For Halloween, Jocelyne bought |36| caramels, |48| lollipops, and |72| small chocolate bars. She wants to make as many bags of candy as possible, with each bag containing the same number of each type of candy.
a) How many bags will Jocelyne be able to make?
b) How many treats of each kind will there be in a bag?
-
Read the problem carefully and decide if finding the GCF is necessary
The goal is to make as many bags as possible with each bag having the same number of each type of candy. This requires finding the GCF. -
Identify the numbers whose GCF is required
Find the greatest common factor of the numbers |36|, |48|, and |72|. The GCF will be equal to the number of bags. -
Calculate the GCF of these numbers
For this step, use any of the methods above. Here is an example using the prime factor strategy.
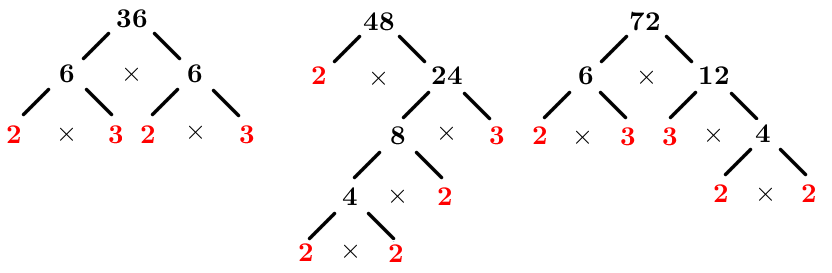
We get
|\begin{align}36&=\color{blue}{2}\times \color{green}{2}\times \color{purple}{3}\times 3\\
48&=\color{blue}{2}\times \color{green}{2}\times 2\times 2\times \color{purple}{3}\\
72&=\color{blue}{2}\times \color{green}{2}\times 2\times \color{purple}{3}\times 3\end{align}|
Therefore, the |GCF(36,48,72)=\color{blue}{2}\times \color{green}{2} \times \color{purple}{3}=12|.
-
Interpret the result
a) Jocelyne will be able to make |12| bags.
b) In each bag, there will be:
-
|36\div 12=3| caramels,
-
|48\div 12=4| lollipops,
-
|72\div 12=6| small chocolate bars.