Fractional notation is a way of writing out rational numbers. This notation includes two types of expressions: fractions and mixed numbers.
A fraction is a rational number expressing an uncompleted division between two whole numbers |a| and |b|, where | b\neq 0|. In other words,
||\left\{ \frac{a}{b} \in \mathbb{Q} \mid a,b \in \mathbb{Z} \ \text{and} \ b \neq 0\right\}||
Generally, fractions are represented like this: ||a/b\qquad \text{or}\qquad \frac{a}{b}||
In this example,
-
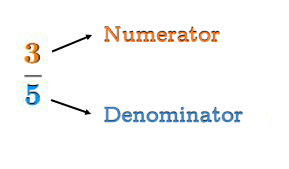
|a| is the numerator, the top number.
-
|b| is the denominator, the bottom number.
-
The line or fraction bar expresses that the numerator is divided by the denominator.
The denominator can never be equal to |0,| because dividing by |0| is undefined in mathematics. The numerator, on the other hand, can be any integer value, positive or negative.
In the following fraction, the numerator is |3| and the denominator is |5.|
A mixed number is a rational number that contains an integer (whole number) part and a fractional part.
Mixed numbers are one way of writing improper fractions.
In the following mixed number, the integer part is |6| and the fractional part is |\dfrac{1}{4}.|
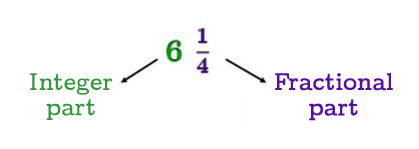
This number reads "|6| and a quarter”. It is one representation of the improper fraction |\dfrac{25}{4}|.
To fully understand fractional notation and be able to use it in context, it is important to understand the different meanings fractions represent.
Fractions can be seen as a part of a whole.
In this example, the denominator refers to the number of equal parts the whole has been divided into.
The numerator refers to the number of equal parts used up.
Keeping in mind the relationship between the numerator and the denominator, we can always construct a fraction from a whole.
Here are two examples of a fraction as a part of a whole.
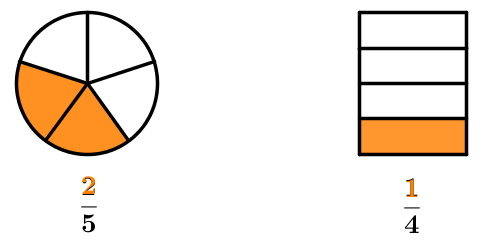
Note: In both examples, note that the number of equal parts in the figure corresponds to the denominator of the fraction, while the number of parts used corresponds to the numerator.
On the other hand, the same whole can be used more than once. For example, several identical cakes can be used at the same party.
The illustration below represents the fraction |\dfrac{7}{3}.|
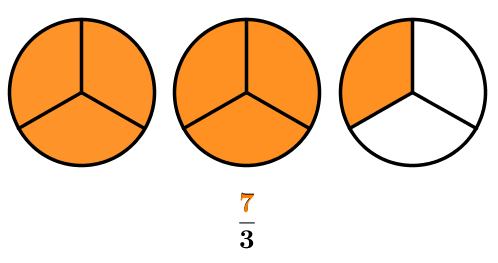
Since the numerator of the fraction is greater than the denominator, more than one whole must be used. However, as in the previous example, notice that the denominator always corresponds to the number of equal parts contained in a single whole, while the numerator corresponds to the number of parts used in total.
In this specific case, we can use a mixed number to write this fraction since the numerator has a greater value than the denominator.
Looking at the illustration, notice that the number |\dfrac{7}{3}| consists of two wholes plus one third of a whole. The mixed number form of this improper fraction is therefore:
||\frac{7}{3}=2 \frac{1}{3}||
Fractions can also be used to compare two quantities of the same kind.
In this example, we are interested in the ratio between the number of green marbles and the number of blue marbles contained in the bag below.
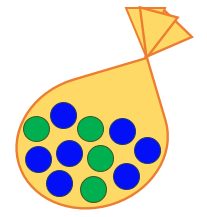
The fraction representing this ratio is: |\dfrac{\color{green}{4}}{\color{blue}{7}}|.
In this case, the fraction means that for every |4| green marbles, there are |7| blue marbles.
This example has a “part to part” relationship and not a “part of a whole” relationship as seen in the previous section.
See also
As mentioned in the definition above, a fraction expresses an unfinished division between two numbers: the numerator and the denominator.
Thus, a fraction can be seen as the simple division of a numerator by a denominator.
The result of this division is the same rational number represented by the fraction written in decimal notation.
Fraction
Dividing the fraction |\dfrac{3}{4}|, results in: ||\dfrac{3}{4}=3\div 4=0{.}75|| Thus, |0{.}75| is the decimal form of the rational number corresponding to |\dfrac{3}{4}.|
Mixed number
Take the fraction |\dfrac{12}{5}.| Dividing the two numbers results in: ||\dfrac{12}{5}=12\div 5=2{.}4|| Thus, |2{.}4| is the decimal form of the rational number corresponding to |\dfrac{12}{5}.|
Performing the division of a fraction results in a number that represents the same quantity, but that is written in a different notation.
Different forms of notation can be used to represent the same quantity. For example:
||\begin{align} {\small\frac{11}{5}} &= 2{\small\frac{1}{5}} && \text{Fraction and mixed number} \\
&= 2{.}2 && \text{Decimal notation} \\
&= 220\ \% && \text{Percentage} \end{align}||
Pour valider ta compréhension des fractions de façon interactive, consulte la MiniRécup suivante :
