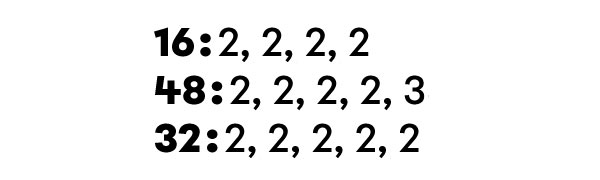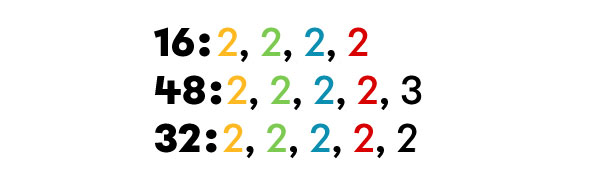The greatest common factor (GCF) is a factor which is shared by two or more numbers. Numbers can have more than one common factor, but the GCF designates the largest one.
To find the GCF using factors, I have to follow these steps:
-
I write the list of factors of each number.
-
I determine the common factors.
-
I identify the largest common factor.
What is the GCF of 16, 48, and 32?
-
I write the list of factors of each number.

-
I determine the common factors.

-
I identify the largest common factor.
I notice that 16 is the greatest common divisor.

The GCF of 16, 48, and 32 is 16.
To find the GCF using prime factorization, I have to follow these steps:
-
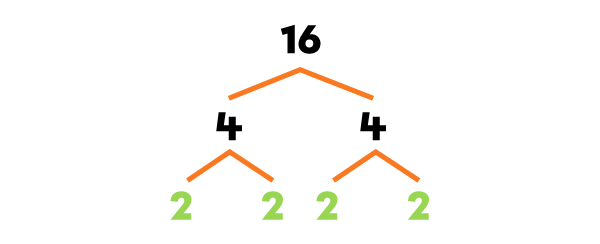
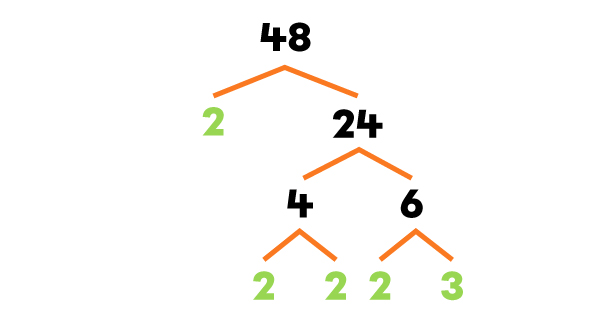
I make a factor tree for each number.
-
I write the prime factorization of each number.
-
I identify the prime factors shared by all the numbers.
-
I calculate the GCF by multiplying the common prime factors together.
What is the GCF of 16, 48, and 32?
|
 |
|
|
|
|
|
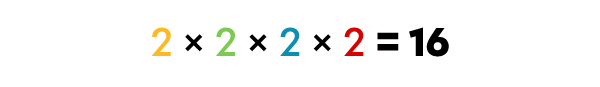
|
The GCF of 16, 48, and 32 is 16.
To find the GCF using a table of common factors, I have to follow these steps:
-
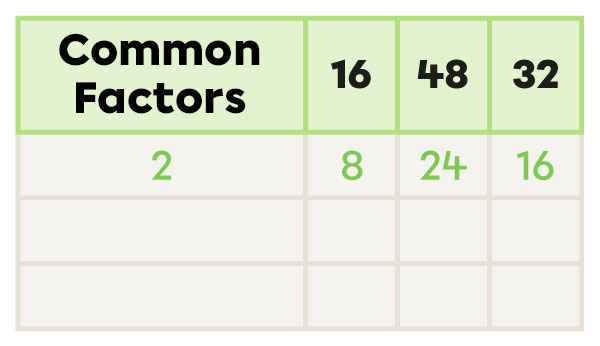
I draw a table with the first column titled Common Factors. The labels of the other columns will correspond to the numbers whose GCF I need to find.
-
I check if there is a common factor between all the numbers. I enter the factor in the Common Factors column and the result of the division under each number.
-
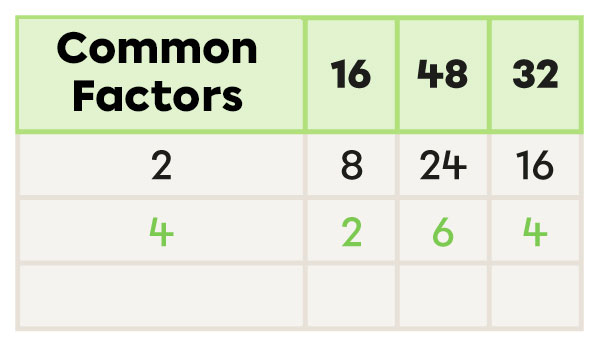
I repeat the process until there is no common factor other than 1.
-
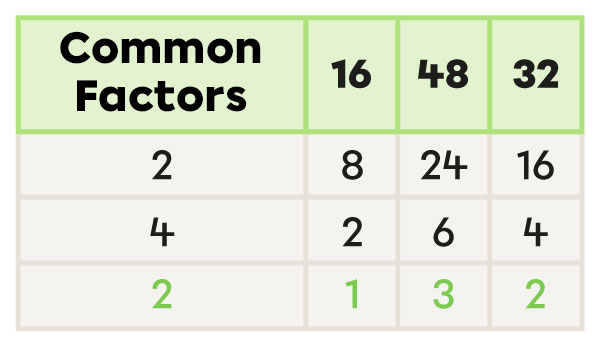
I calculate the GCF by multiplying the common factors in the first column.
What is the GCF of 16, 48, and 32?
|

|
|
|
|
  |
|
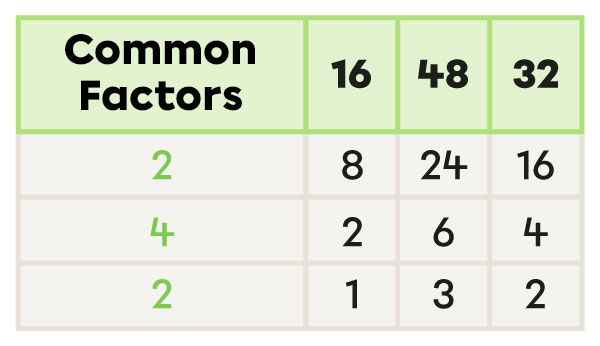
2 x 4 x 2 = 16 |
The GCF of 16, 48, and 32 is 16.