Le plus grand commun diviseur (PGCD) est un diviseur qui est commun à deux ou à plusieurs nombres. Des nombres peuvent avoir plus d’un diviseur commun, mais le PGCD ne désigne que le plus grand d’entre eux.
Pour trouver le PGCD à l’aide de la méthode des diviseurs, je dois suivre les étapes suivantes :
-
J’écris la liste des diviseurs de chacun des nombres.
-
Je repère les diviseurs communs.
-
J’identifie le plus grand parmi ces diviseurs.
Quel est le PGCD de 16, 48 et 32?
-
J’écris la liste des diviseurs de chacun des nombres.

-
Je repère les diviseurs communs.

-
J’identifie le plus grand parmi ces diviseurs.
Je remarque que 16 est le plus grand diviseur commun.

Le PGCD de 16, 48 et 32 est 16.
Pour trouver le PGCD à l’aide des facteurs premiers, je dois suivre les étapes suivantes :
-
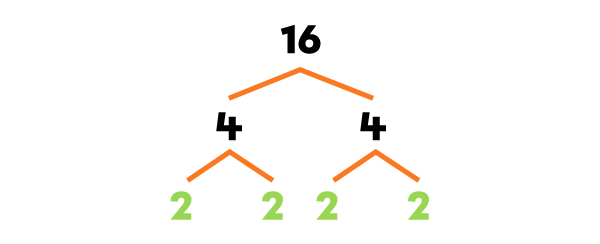
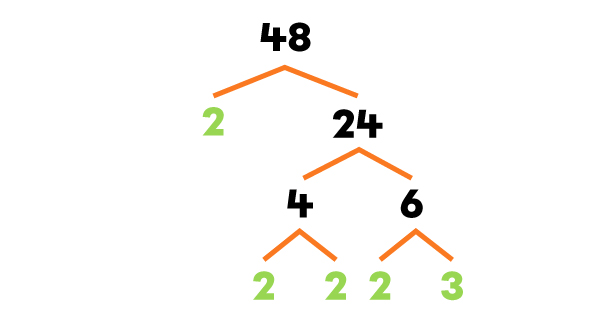
Je fais l’arbre des facteurs de chaque nombre.
-
J’écris les facteurs premiers de chaque nombre.
-
J’identifie les facteurs premiers communs entre tous les nombres.
-
Je calcule le PGCD en multipliant ensemble les facteurs premiers communs.
Quel est le PGCD de 16, 48 et 32?
|
 |
|

|
|
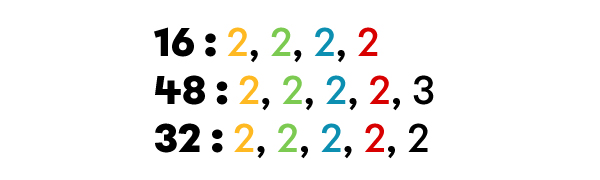
|
|
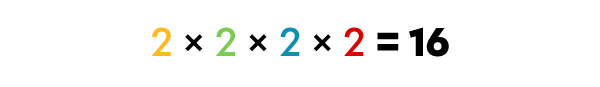
|
Le PGCD de 16, 48 et 32 est 16.
Pour trouver le PGCD à l’aide d’un tableau des diviseurs communs, je dois suivre les étapes suivantes :
-
Je trace un tableau dont le titre de la première colonne est Diviseurs communs. Le titre des autres colonnes correspond aux nombres dont on veut trouver le PGCD.
-
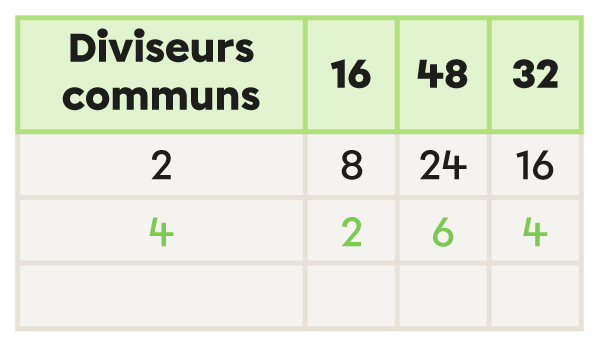
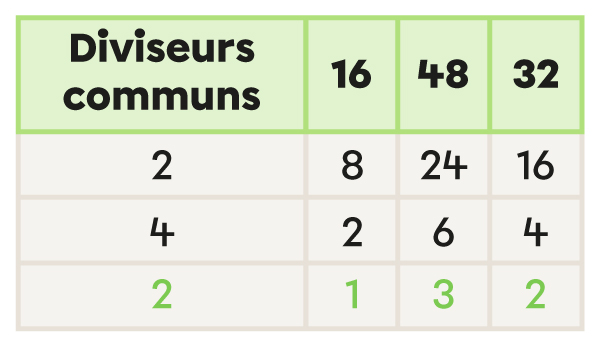
Je vérifie s’il existe un diviseur commun pour tous les nombres. J’inscris le diviseur dans la colonne Diviseurs communs et la réponse de la division sous chaque nombre.
-
Je recommence jusqu’à ce qu’il n’y ait plus de diviseur commun autre que 1.
-
Je calcule le PGCD en multipliant les diviseurs communs de la première colonne.
Quel est le PGCD de 16, 48 et 32?
|

|
|

|
|
 |
|
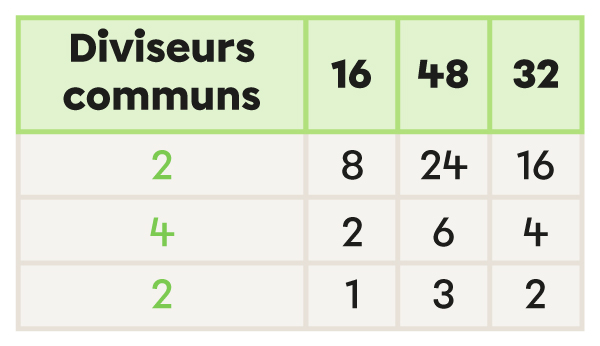
2 x 4 x 2 = 16 |
Le PGCD de 16, 48 et 32 est 16.