Le Plus Grand Commun Diviseur (PGCD) entre deux nombres ou plus est le plus grand entier naturel qui divise simultanément tous ces nombres.
Lorsque 2 nombres ou plus ont un PGCD égal à |1,| on dira de ces nombres qu'ils sont premiers entre eux ou copremiers.
Il existe plusieurs façons de déterminer le PGCD entre deux nombres ou plus. Cette fiche proposera des méthodes permettant d'y arriver en plus de présenter les principaux types de mises en situation impliquant la recherche d'un PGCD.
Les méthodes présentées ci-dessous ne concernent que le PGCD. Pour savoir comment trouver le PPCM et le PGCD de deux ou plusieurs nombres simultanément, visite la fiche suivante.
Comme nous cherchons le plus grand commun diviseur, on peut simplement dresser la liste des diviseurs des nombres étudiés et repérer le plus grand des diviseurs communs à ces nombres. Cette méthode simple convient surtout lorsqu'on a de petits nombres.
-
Dresser la liste des diviseurs de chacun des nombres.
-
Repérer les diviseurs communs.
-
Choisir le plus grand de ces diviseurs.
Détermine le PGCD de |30| et |45.|
-
Dresser la liste des diviseurs de chacun des nombres ||\begin{align}30&:\left\{1, 2, 3, 5, 6, 10, 15, 30\right\}\\45&:\left\{1, 3, 5, 9, 15, 45\right\}\end{align}||
-
Repérer les diviseurs communs ||\begin{align}30&:\left\{\color{#3a9a38}{1}, 2, \color{#3a9a38}{3}, \color{#3a9a38}{5}, 6, 10, \color{#3a9a38}{15}, 30\right\}\\45&:\left\{\color{#3a9a38}{1}, \color{#3a9a38}{3}, \color{#3a9a38}{5}, 9, \color{#3a9a38}{15}, 45\right\}\end{align}||
-
Choisir le plus grand de ces diviseurs
On remarque que |\color{#3a9a38}{15}| est le plus grand diviseur commun.
Réponse : |PGCD(30,45)=15|
Détermine le PGCD de |15| et |26.|
-
Dresser la liste des diviseurs de chacun des nombres ||\begin{align}15&:\left\{1, 3, 5, 15\right\}\\26&:\left\{1, 2, 13, 26\right\}\end{align}||
-
Repérer les diviseurs communs ||\begin{align}15&:\left\{\color{#3a9a38}{1}, 3, 5, 15\right\}\\26&:\left\{\color{#3a9a38}{1}, 2, 13, 26\right\}\end{align}||
-
Choisir le plus grand de ces diviseurs
On remarque que |\color{#3a9a38}{1}| est le plus grand diviseur commun.
Réponse : |PGCD(15,26)=1|
Remarque : On dit de |15| et de |26| qu'ils sont premiers entre eux ou copremiers.
Détermine le PGCD de |12,| |36| et |60.|
-
Dresser la liste des diviseurs de chacun des nombres ||\begin{align}12&:\left\{1, 2, 3, 4, 6, 12\right\}\\36&:\left\{1, 2, 3, 4, 6, 9, 12, 18, 36\right\}\\60&:\left\{1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 \right\}\end{align}||
-
Repérer les diviseurs communs ||\begin{align}12&:\left\{\color{#3a9a38}{1}, \color{#3a9a38}{2}, \color{#3a9a38}{3}, \color{#3a9a38}{4}, \color{#3a9a38}{6}, \color{#3a9a38}{12}\right\}\\36&:\left\{\color{#3a9a38}{1}, \color{#3a9a38}{2}, \color{#3a9a38}{3}, \color{#3a9a38}{4}, \color{#3a9a38}{6}, 9, \color{#3a9a38}{12}, 18, 36\right\}\\60&:\left\{\color{#3a9a38}{1}, \color{#3a9a38}{2}, \color{#3a9a38}{3}, \color{#3a9a38}{4}, 5, \color{#3a9a38}{6}, 10, \color{#3a9a38}{12}, 15, 20, 30, 60\right\}\end{align}||
-
Choisir le plus grand de ces diviseurs
On remarque que |\color{green}{12}| est le plus grand diviseur commun.
Réponse : |PGCD(12,36,60)=12|
Cette méthode consiste à diviser simultanément les nombres étudiés par des diviseurs premiers. Le PGCD sera alors le produit de ces diviseurs premiers. Cette méthode est plus rapide et efficace lorsque l'on cherche le PGCD entre deux grands nombres.
-
Tracer un tableau dont le titre de la première colonne sera Diviseurs premiers. Les titres des autres colonnes seront les nombres étudiés.
-
Tenter de diviser simultanément les nombres étudiés par des diviseurs premiers. On peut commencer par |2|, puis par |3|, |5|, |7| et ainsi de suite. On poursuit la division jusqu'à ce qu'il n'y ait plus de diviseurs communs.
-
Calculer le PGCD en multipliant les diviseurs premiers de la première colonne.
Calcule le PGCD de |36| et |90|.
-
Tracer un tableau dont le titre de la première colonne sera Diviseurs premiers. Les titres des autres colonnes seront les nombres étudiés.
-
Tenter de diviser simultanément les nombres étudiés par des diviseurs premiers. On poursuit la division jusqu'à ce qu'il n'y ait plus de diviseurs communs.
| Diviseurs communs |
|36| | |90| |
|---|---|---|
| |\color{#3b87cd}{2}| | |18| | |45| |
| |\color{#3b87cd}{3}| | |6| | |15| |
| |\color{#3b87cd}{3}| | |2| | |5| |
-
Calculer le PGCD en multipliant les diviseurs premiers de la première colonne. ||\begin{align}PGCD(36,90)&=\color{#3b87cd}{2}\times \color{#3b87cd}{3}\times \color{#3b87cd}{3}\\ &=18\end{align}||
Cette méthode consiste à faire la factorisation première de tous les nombres et d'écrire le PGCD sous la forme d'un produit des facteurs commun. Cette méthode est très polyvalente.
-
Décomposer chaque nombre en produit de facteurs premiers.
-
Repérer les facteurs communs.
-
Écrire le PGCD comme un produit de ces facteurs communs.
Les facteurs communs doivent être communs à tous les nombres dont on cherche le PGCD. Prenons, par exemple, la recherche du PGCD de |60,\ 84| et |140.|
La factorisation première de ces nombres est donnée ci-dessous.
|\begin{align}60&=2\times 2\times 3\times 5\\
84&=2\times 2\times 3\times 7\\
140&=2\times 2\times 5\times 7\end{align}|
Ici, le |3|, le |5| et le |7| ne sont pas des facteurs communs, car ils n'apparaissent que dans deux des trois nombres.
De plus, si un facteur commun revient plus d'une fois, on doit l'inclure le même nombre de fois dans le PGCD. Comme le facteur |2| est commun à tous les nombres deux fois, il doit être inclus deux fois dans le PGCD.
Nous aurons donc que |PGCD(60,84,140)=2\times 2=4|.
Détermine le PGCD de |24| et |84.|
-
Décomposer chaque nombre en produit de facteurs premiers
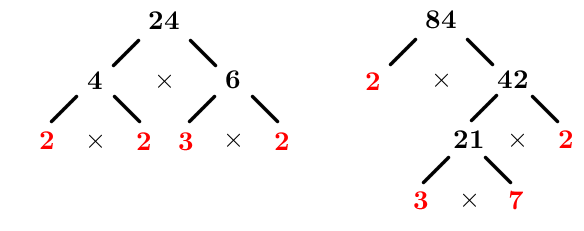
On obtient ceci. ||\begin{align}24&=2\times 2\times 2\times 3 \\84&=2\times 2\times 3\times 7 \end{align}||
-
Repérer les facteurs communs ||\begin{align}24&=\color{#3a9a38}{2}\times \color{#3b87cd}{2}\times 2\times \color{#560fa5}{3} \\84&=\color{#3a9a38}{2}\times \color{#3b87cd}{2}\times \color{#560fa5}{3}\times 7 \end{align}||
-
Écrire le PGCD comme un produit de ces facteurs communs ||\begin{align}PGCD(24,84)&=\color{#3a9a38}{2}\times\color{#3b87cd}{2}\times\color{#560fa5}{3}\\ &=12\end{align}||
Détermine le PGCD de |40,| |60| et |75.|
-
Décomposer chaque nombre en produit de facteurs premiers
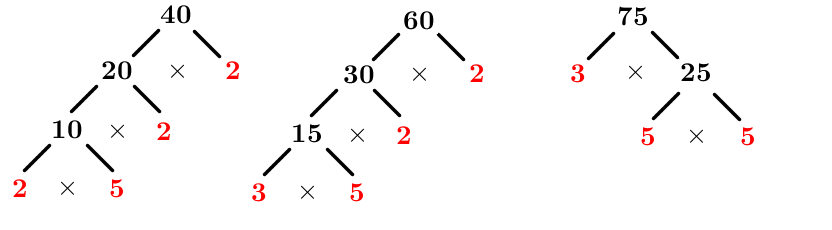
On obtient ceci. ||\begin{align}40&=2\times 2\times 2\times 5 \\60&=2\times 2\times 3\times 5\\75&=3\times 5\times 5\end{align}||
-
Repérer les facteurs communs ||\begin{align}40&=2\times 2\times 2\times \color{#3a9a38}{5} \\60&=2\times 2\times 3\times \color{#3a9a38}{5}\\75&=3\times \color{#3a9a38}{5}\times 5\end{align}||
-
Écrire le PGCD comme un produit de ces facteurs communs ||PGCD(40,60,75)=\color{#3a9a38}{5}||
Dans certaines situations, on devra utiliser le PGCD sans que ce soit demandé explicitement. Voici quelques types de situation où l'on doit chercher le PGCD pour trouver la réponse.
-
Trouver le plus grand nombre de groupes équivalents qu'il est possible de former à partir de différents nombres d'éléments.
-
Trouver le plus grand nombre de collations identiques qu'il est possible de former à partir de différents nombres d'ingrédients.
-
Trouver le plus grand nombre d'individus qu'il est possible de placer dans des groupes de même grandeur.
Pour résoudre ces situations avec succès, voici comment procéder.
-
Lire attentivement le problème et déceler si on doit utiliser la recherche d'un PGCD.
-
Repérer les différents nombres dont on cherche le PGCD.
-
Calculer le PGCD de ces nombres.
-
Interpréter le résultat.
Dans un restaurant, on a 2 réservations de groupes pour la soirée : un groupe de |60| personnes et un groupe de |90| personnes. On souhaite les répartir à des tables où pourront s’asseoir le plus de personnes possible ensemble, mais on veut qu’il y ait le même nombre de personnes à chaque table. Combien y aura-t-il de personnes assises à chaque table?
-
Lire attentivement le problème et déceler si on doit utiliser la recherche d'un PGCD
Comme nous pouvons le voir, on demande de trouver le plus grand nombre de personnes il est possible d'asseoir à des tables comprenant le même nombre de personne. On devra utiliser la recherche d'un PGCD. -
Repérer les différents nombres dont on cherche le PGCD
On devra trouver le plus grand commun diviseur entre |60| et |90.| -
Calculer le PGCD de ces nombres
Pour cette étape, on peut utiliser la méthode de son choix. Utilisons la méthode des diviseurs. ||\begin{align}60&:\left\{\color{#3a9a38}{1}, \color{#3a9a38}{2}, \color{#3a9a38}{3}, 4, \color{#3a9a38}{5}, \color{#3a9a38}{6}, \color{#3a9a38}{10}, 12, \color{#3a9a38}{15}, 20, \underline{\color{#3a9a38}{30}}, 60\right\}\\90&:\left\{\color{#3a9a38}{1}, \color{#3a9a38}{2}, \color{#3a9a38}{3}, \color{#3a9a38}{5}, \color{#3a9a38}{6}, 9, \color{#3a9a38}{10}, \color{#3a9a38}{15}, 18, \underline{\color{#3a9a38}{30}}, 45, 90\right\}\end{align}||On remarque que |PGCD(60,90)=\color{#3a9a38}{30}.| -
Interpréter le résultat
|30| est le plus grand nombre de personnes qu'il est possible d'asseoir à des tables ayant le même nombre de personnes si on a un groupe de |60| et un groupe de |90.|
Pour l'halloween, Jocelyne a acheté |36| caramels, |48| suçons et |72| petites barres de chocolat. Elle veut faire le plus de sacs de bonbons possibles tout en ayant le même nombre de friandises de chaque sorte dans les sacs.
a) Combien de sacs Jocelyne pourra-t-elle faire?
b) Combien de friandises de chaque sorte y aura-t-il dans un sac?
-
Lire attentivement le problème et déceler si on doit utiliser la recherche d'un PGCD
On veut créer le plus de sacs de bonbons possibles tout en ayant le même nombre de friandises de chaque sorte dans les sacs. On devra utiliser la recherche d'un PGCD. -
Repérer les différents nombres dont on cherche le PGCD
On devra trouver le plus grand commun diviseur entre |36,| |48| et |72.| Le PGCD représentera le nombre de sacs. -
Calculer le PGCD de ces nombres
Pour cette étape, on peut utiliser la méthode de son choix. Utilisons la méthode des facteurs premiers.
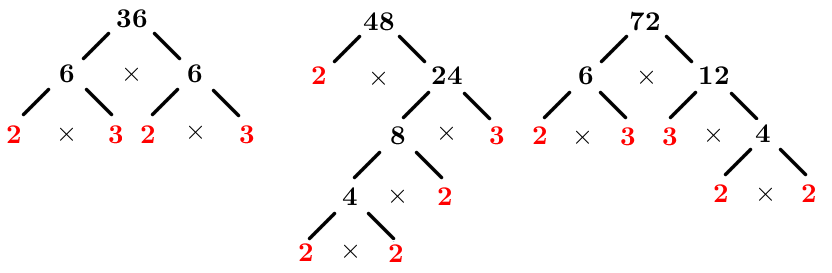
On obtient ceci. ||\begin{align}36&=\color{#3b87cd}{2}\times \color{#3a9a38}{2}\times \color{#560fa5}{3}\times 3\\ 48&=\color{#3b87cd}{2}\times \color{#3a9a38}{2}\times 2\times 2\times \color{#560fa5}{3}\\ 72&=\color{#3b87cd}{2}\times \color{#3a9a38}{2}\times 2\times \color{#560fa5}{3}\times 3\end{align}||On remarque que |PGCD(36,48,72)=\color{#3b87cd}{2}\times \color{#3a9a38}{2} \times \color{#560fa5}{3}=12.|
-
Interpréter le résultat
a) Jocelyne pourra faire |12| sacs.
b) Dans un sac, on retrouvera :
-
|36\div 12=3| caramels,
-
|48\div 12=4| suçons,
-
|72\div 12=6| petites barres de chocolat.