To multiply a fraction by a natural number, put the natural number over |1.| Multiply the two numerators together and then multiply the two denominators together.
Follow these steps to multiply a fraction by a natural number using multiplication:
-
I convert the natural number into a fraction by putting it over |1.|
-
I multiply the numerators together.
-
I multiply the denominators together.
Make sure to read the given instructions carefully. The answer may have to be written as a mixed number or as an irreducible fraction.
|4 × \dfrac{2}{12} = ?|
|
|\dfrac{2}{12} × \dfrac{4}{1} =\ ?| |
|
|\dfrac{\color{red}2}{12} × \dfrac{\color{red}4}{1} = \dfrac{\color{red}8}{?}| |
|
|\dfrac{2}{\color{red}1\color{red}2} × \dfrac{4}{\color{red}1} = \dfrac{8}{\color{red}1\color{red}2}| |
|4 × \dfrac{2}{12} = \dfrac{8}{12}|
Multiplying fractions is the same as adding the fractions together the number of times written in the multiplication. When fractions have the same denominator, add the numerators together to get the final result.
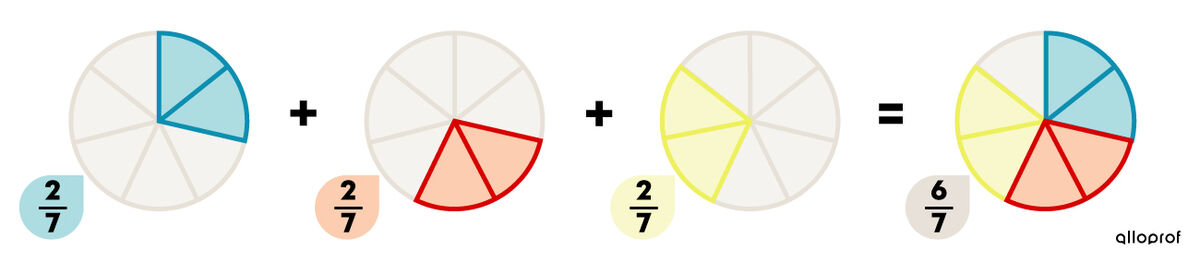
To do the multiplication |\dfrac{2}{7} × 3| or |3 × \dfrac{2}{7}|, the fraction |\dfrac{2}{7}| must be added together |3| times.
Follow these steps to multiply a fraction by a natural number using repeated addition:
-
I write a series of repeated additions using the fraction.
-
I add the numerators.
-
I write the denominator of the multiplied fraction as the denominator of the answer.
Make sure to read the instructions carefully. The answer may need to be written as a mixed number or as an irreducible fraction.
|\dfrac{2}{12} × 4 = ?|
|
|\dfrac{2}{12} + \dfrac{2}{12} + \dfrac{2}{12} + \dfrac{2}{12} =\ ?| |
|
|{\dfrac{\color{red}2}{12}} + {\dfrac{\color{red}2}{12}} + {\dfrac{\color{red}2}{12}} + {\dfrac{\color{red}2}{12}} = {\dfrac{\color{red}8}{?}}| |
|
|{\dfrac{2}{\color{red}1\color{red}2}} + {\dfrac{2}{\color{red}1\color{red}2}} + {\dfrac{2}{\color{red}1\color{red}2}} + {\dfrac{2}{\color{red}1\color{red}2}} = {\dfrac{8}{\color{red}1\color{red}2}}| |
|\dfrac{2}{12} × 4 = \dfrac{8}{12}|