A fraction is irreducible when the numerator and the denominator share only |1| as a common factor. Thus, the fraction has been “reduced” to its simplest form.
A fraction can be simplified or “reduced” by dividing the numerator and the denominator by the same number.

The fraction obtained can sometimes be further simplified.
For example, the fraction |\dfrac{12}{15}| can be simplified again.
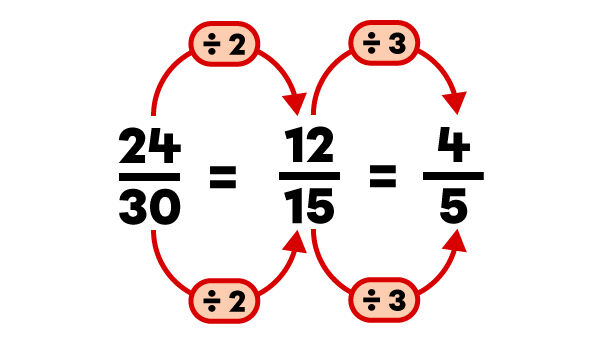
When the numerator and the denominator no longer share a common factor, the fraction is irreducible.
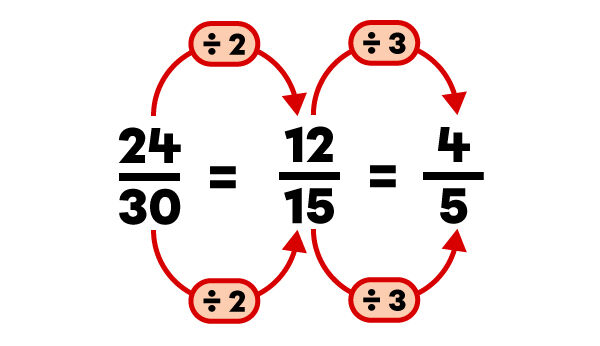
In this example, |4| and |5| only share |1| as a common factor. The irreducible fraction is |\dfrac{4}{5}| since |4| divided by |1| equals |4| and |5| divided by |1| equals |5|. Thus, the fraction has been reduced to its simplest form.
A simplified fraction must always be equivalent to the initial fraction.

-
I find a common factor for the numerator and the denominator.
-
I divide the numerator by the number.
-
I divide the denominator by the number.
-
I repeat steps |1|, |2| and |3| until no common factor exists other than |1.|
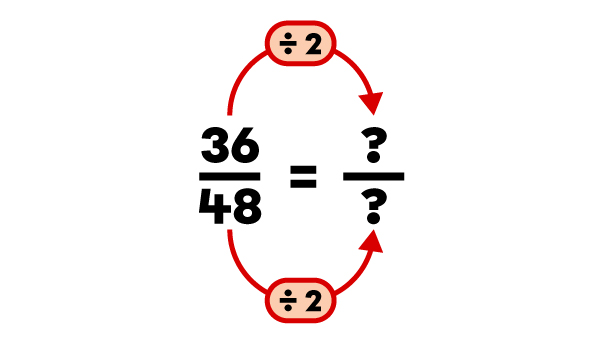
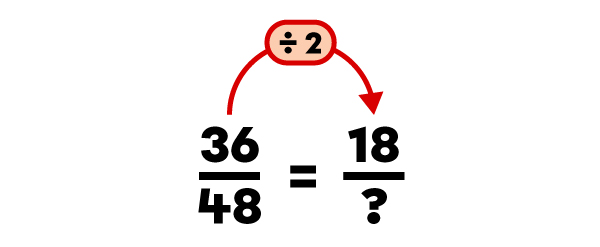
Reduce the fraction |\dfrac{36}{48}| to its lowest terms.
|
|
|
|
|
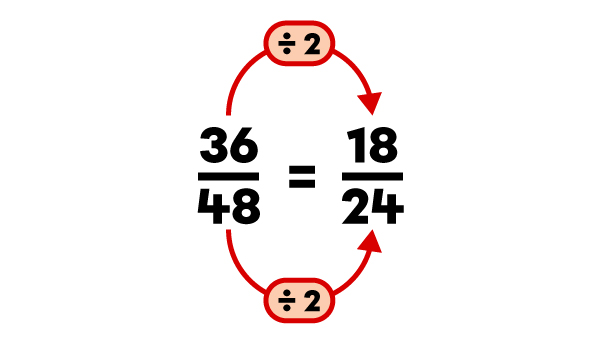
|
|
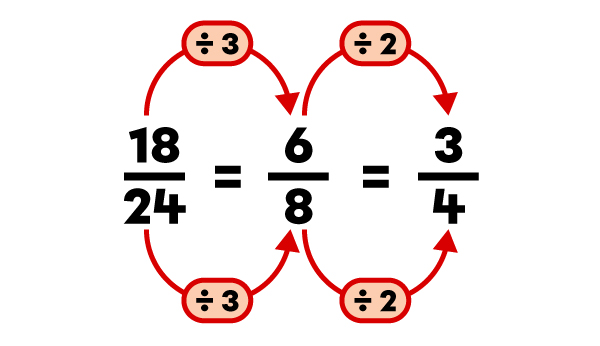
|
The fraction |\dfrac{3}{4}| is the irreducible equivalent of |\dfrac{36}{48}.|
-
I find the GCF of the numerator and the denominator.
-
I divide the numerator by the GCF.
-
I divide the denominator by the GCF.
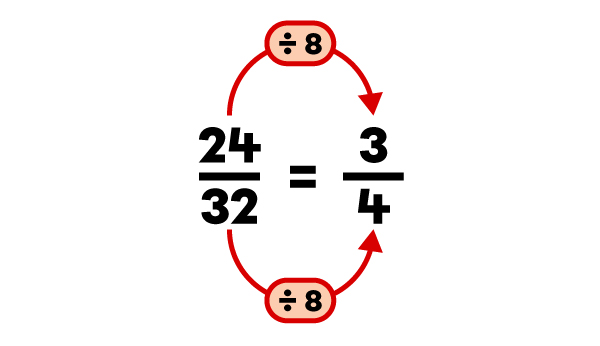
Reduce the fraction |\dfrac{24}{32}| to its lowest terms.
|
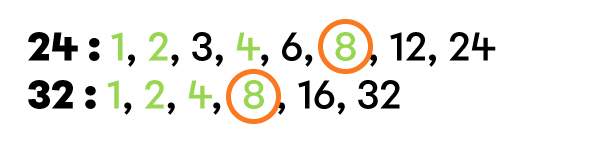
|
|
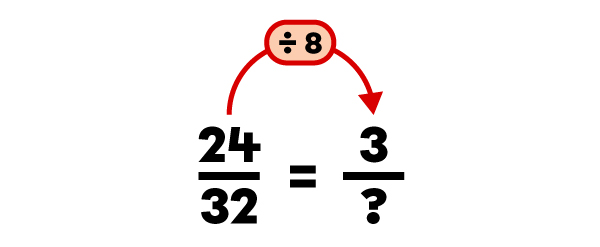
|
|
|
The fraction |\dfrac{3}{4}| is the irreducible equivalent of |\dfrac{24}{32}.|