Multiplication and division can be performed with positive numbers, but also with negative numbers. It's important to make sure you're comfortable with the set of integers. There is a close link between the multiplication and division of positive and negative numbers, since they are inverse operations. Both operations follow the sign rule.
The sign rule is used to determine the sign of the result of a multiplication or division.
-
If the 2 numbers being multiplied or divided have the same sign, the answer is positive.
-
If the 2 numbers being multiplied or divided have opposite signs, the answer is negative.
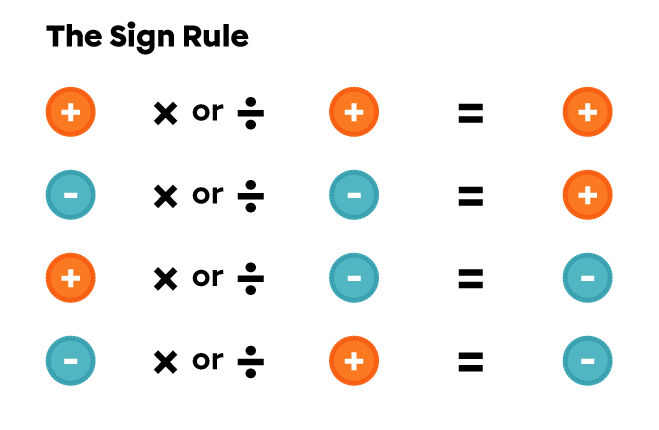
Note: The sign rule also applies when the 2 signs are placed together in a chain of operations.
Here's the reasoning behind the different outcomes produced by using the sign rule. The explanation is given for multiplication, but the same principle applies to division.
We start from the principle that |2| positive numbers multiplied together give an equally positive product. ||3 \times 2 = 6||
A Positive Number Multiplied by a Negative Number
We want to find the result of the operation |3 \times -2.| We start at |3 \times 2,| and gradually decrease the 2nd factor. We find that, each time the 2nd factor decreases by |\boldsymbol{\color{#ff55c3}1},| the product decreases by |\boldsymbol{\color{#3a9a38}3}.| We can therefore determine that when we multiply a positive number with a negative number, the product is negative.

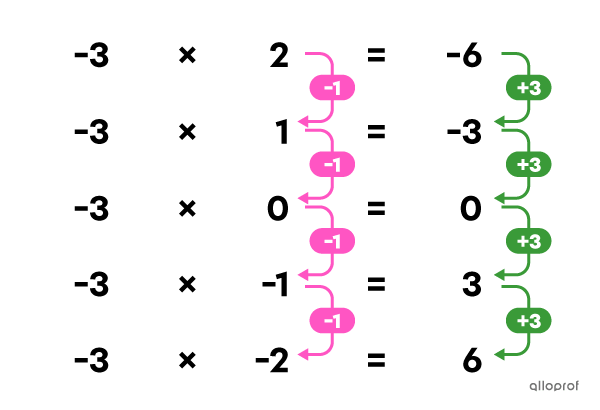
A Negative Number Multiplied by a Positive Number
We want to find the result of the operation |-3 \times 2.| We start at |3 \times 2,| and progressively decrease the 1st factor. We find that, each time the 1st factor decreases by |\boldsymbol{\color{#ff55c3}1},| the product decreases by |\boldsymbol{\color{#3a9a38}2}.| We can therefore determine that when we multiply a negative number with a positive number, the product is negative.

A Negative Number Multiplied by a Negative Number
We want to find the result of the operation |-3 \times -2.| We start at |-3 \times 2.| We have determined that the result of this calculation is negative. Gradually decrease the 2nd factor. We find that, each time the 2nd factor decreases by |\boldsymbol{\color{#ff55c3}1},| the product increases by |\boldsymbol{\color{#3a9a38}3}.| We can therefore determine that when we multiply a negative number with a negative number, the product is positive.
To multiply or divide positive and negative numbers, first perform the operation without taking the signs into account, then determine the sign of the answer using the sign rule. This technique applies equally to multiplying decimal numbers and fractions and to dividing decimal numbers and fractions.
Find the result of the multiplication |-15 \times 3.|
We start by finding the product, ignoring the signs.
||15 \times 3 = 45||
Since the 2 factors have opposite signs, the result is negative, according to the sign rule.
Answer: The result of the multiplication |-15 \times 3| is |-45.|
The sign rule also applies to fractions, since fractions represent divisions. By convention, we put the "-" sign in front of the fraction or in the numerator, but not in the denominator. ||\begin{align}\dfrac{-15}{-4}\ &\Rightarrow\ \dfrac{15}{4}\\[3pt] \dfrac{2}{-3}\ &\Rightarrow\ -\dfrac{2}{3}\end{align}||
If there is a chain of operations with several multiplications or divisions, and you want to determine the sign of the final result, count the number of "-" signs. If there is an even number, the result is positive. If there is an odd number, the result is negative.
Find the result of the chain of operations |-452 \div -16 \times 12 \times 2 \div -15.|
First, we perform the calculations, ignoring the signs.||\begin{align}&452 \div 16 \times 12 \times 2 \div 15\\=\ &28.25 \times 12 \times 2 \div 15\\=\ &339 \times 2 \div 15\\=\ &678 \div 15\\=\ &45.2 \end{align}||
Since there are 3 negative numbers in the chain of operations |(-452,| |-16| and |-15),| the result is negative.
Answer: The result of the chain of operations |-452 \div -16 \times 12 \times 2 \div -15| is |-45.2.|