A number system is a set of symbols (digits) that are assembled according to precise writing rules, making it possible to write, read and express numbers.
Throughout history, dozens of numeration systems have been invented to meet different needs. There are additive number systems, such as Roman numerals, and positional systems, such as decimal numeration (base 10), which are used in everyday life. Since the creation of electronic circuits and computers, binary (base 2) and hexadecimal (base 16) systems, which are also positional systems, have become essential. What exactly is a base?
A base, in a positional number system, is the number of symbols (digits) that are used to represent numbers.
A base |10| number system (decimal numeration) uses |10| digits from |0| to |9,| while a base |2| number system (binary numeration) uses only |2| digits, zero |(0)| and one |(1).|
Writing numbers as we know it uses Indo-Arabic digits, namely |0,| |1,| |2,| |3,| |4,| |5,| |6,| |7,| |8,| |9.| In theory, this form of writing only applies to writing numbers in base |10.|
However, to make things easier to understand, these same digits will be used throughout this concept sheet. To distinguish between the different bases used, we will use a subscript for reference purposes: ||576_\boldsymbol{\color{#333fb1}{12}}=576\ \text{base}\ \boldsymbol{\color{#333fb1}{12}}||
Since many different forms of number writing existed around |3500| BC, humans at that time had to use the means at their disposal to count. In this case, they used the fingers of their left hand (5) and the phalanges of their right hand (12). So, 1 finger of the left hand was equal to all 12 phalanges of the right hand.
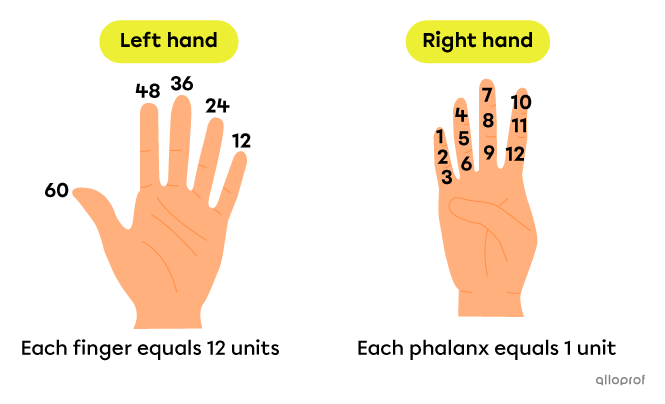
Source : Ifrah, G. (1994). Histoire universelle des chiffres. Éditions Robert Laffont.
For example, ||\begin{align}\text{left index raised}+{1^\text{st}\ \text{right index phalange}}&=4\times\underbrace{\boldsymbol{\color{#333FB1}{12}}^1}_{\text{place value}}+10\times\underbrace{\boldsymbol{\color{#333FB1}{12}}^0}_{\text{place value}}\\&=4\times\boldsymbol{\color{#333FB1}{12}}+10\times\boldsymbol{\color{#333FB1}{1}}\\&=48+10\\&=58\end{align}||
Just like with base |10| numeration, we can use the place value position system and the expanded form of the numbers to correctly interpret the value of a number in base |12.|
This quantification method using fingers and phalanges brought about the duodecimal system, in base |12.|
As well, this way of counting using fingers and phalanges is also related to the sexagesimal system, in base |60.|
Taking all |5| fingers of the left hand and all |12| phalanges of the right hand into consideration, there are a total of |60| possibilities: |(5 \times 12 =60).|
In today's society, this base is found in our units of time: seconds, minutes and hours.
How many seconds are there in 5 hours 17 minutes and 34 seconds? ||\begin{align}(5\ \text{h}\ 17\ \text{min} \ 34 \ \text{s})_{\boldsymbol{\color{#333FB1}{60}}}&=5\times\underbrace{\boldsymbol{\color{#333FB1}{60}}^2}_{\text{place value}}+17\times\underbrace{\boldsymbol{\color{#333FB1}{60}}^1}_{\text{place value}}+34\times\underbrace{\boldsymbol{\color{#333FB1}{60}}^0}_{\text{place value}}\\&=5\times\boldsymbol{\color{#333FB1}{60\times60}}+17\times\boldsymbol{\color{#333FB1}{60}}+34\times\boldsymbol{\color{#333FB1}{1}}\\&=18\ 000+1020+34\\&=19\ 054\ \text{s}\end{align}||
However, this method had one major drawback, namely the representation of numbers with very large values, such as |5\ 458\ 384.| To overcome this difficulty, further discoveries were made in later centuries.
When large quantities had to be represented, 10 fingers and 2 hands were not enough. So, between the 11th and 14th century BC, a new system emerged in China–the decimal system, or base 10.
Accustomed to counting with 10 fingers, it seemed natural to use 10. However, the introduction and the official use of the number 0 would not happen until the 5th century AD.
Along with the arrival of the value zero came the idea of grouping elements to better represent them. A group of 10 ones became a ten; a group of 10 tens became a hundred, and so on.
For more information, the concept sheets on place value positions and numbers in expanded form are available in the virtual library.
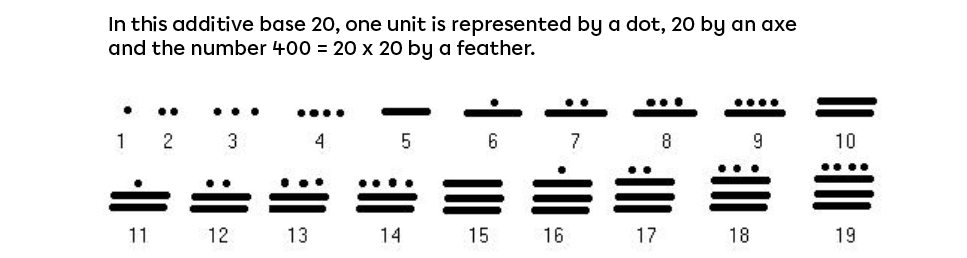
The Mayan people also established their calendar in the 5th century using base 20. Why? Not only did they use their 10 fingers, but also their 10 toes!
Since this is not a base 10 system, the symbols used to represent various quantities are not the digits as we know them.
Additionally, numbers in this system were not written from left to right, but from the bottom upwards.
Just like numeration in base 10, the place value positions system and the expanded form of numbers can be used to accurately interpret their respective values.
Using today’s digits, determine the number that corresponds to this image.
||\begin{align}\text{This number}_{\boldsymbol{\color{#333FB1}{20}}}&=11\times\underbrace{\boldsymbol{\color{#333FB1}{20}}^2}_{\text{place value}}+6\times\underbrace{\boldsymbol{\color{#333FB1}{20}}^1}_{\text{place value}}+16\times\underbrace{\boldsymbol{\color{#333FB1}{20}}^0}_{\text{place value}}\\&=11\times\boldsymbol{\color{#333FB1}{20\times20}}+6\times\boldsymbol{\color{#333FB1}{20}}+16\times\boldsymbol{\color{#333FB1}{1}}\\&=4400+120+16\\&=4536_{10}\ \text{is its decimal value}\end{align}||
Unlike the other bases, the base 2 binary system is quite recent. Though it was actually discovered in the late 17th century, it has really only been heavily used since the early 20th century.
This way of coding information is the only method understood by the various electronic components of a computer. Generally associated with bits (from the term “binary information digits”), this code has only two symbols: 0 and 1.
To standardize computer coding, these bits were combined into groups of 8 to form bytes. Each byte is associated with a digit, a letter, a punctuation symbol, etc. In other words, each byte is associated with a specific character in the Latin alphabet. Here is an overview of the table of characters used by the ISO/IEC 8859-1 code, namely the “computer alphabet” according to byte coding.
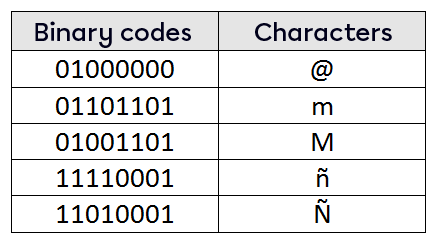
Just like numeration in base 10, the place value position system and the expanded form of numbers can be used to accurately interpret their respective values.
Since each character has its own unique byte, a decimal value can be derived. Moreover, this decimal value often corresponds to universal shortcut keys.
What is the decimal value of this character?
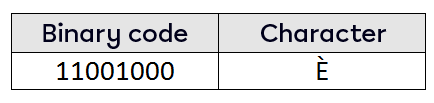
||\begin{align}11001000_{\boldsymbol{\color{#333FB1}{2}}}&=1\times\underbrace{\boldsymbol{\color{#333FB1}{2}}^7}_{\text{place value}}+1\times\underbrace{\boldsymbol{\color{#333FB1}{2}}^6}_{\text{place value}}+1\times\underbrace{\boldsymbol{\color{#333FB1}{2}}^3}_{\text{place value}}\\&=1\times\boldsymbol{\color{#333FB1}{2\times2\times2\times2\times2\times2\times2}}+1\times\boldsymbol{\color{#333FB1}{2\times2\times2\times2\times2\times2}}+1\times\boldsymbol{\color{#333FB1}{2\times2\times2}}\\&=128+64+8\\&=200_{10}\ \text{is its place value position}\end{align}||
It should be noted that the |0s| were deliberately eliminated from the calculations since the zero value does not affect the final answer.
However, with endless sequences of |0|s and |1|s, it is easy to make a mistake. If an error is made, the incorrect character is obtained and the entire string of code must be verified to find the problem. To overcome this difficulty, the base |16| system was introduced to computer languages.
By definition, all numbers from |0| to |15| inclusively can be used to form hexadecimal code. However, this could be a problem since there could only be one character per position. The following naming system was adopted.||\begin{align}0&=0&4&=4&8&=8&12&=C\\1&=1&5&=5&9&=9&13&=D\\2&=2&6&=6&10&=A&14&=E\\3&=3&7&=7&11&=B&15&=F\end{align}||What is the decimal value of this character?

||\begin{align}\text{CA}_{\boldsymbol{\color{#333FB1}{16}}}&=C\times\underbrace{\boldsymbol{\color{#333FB1}{16}}^1}_{\text{place value}}+A\times\underbrace{\boldsymbol{\color{#333FB1}{16}}^0}_{\text{place value}}\\&=12\times\underbrace{\boldsymbol{\color{#333FB1}{16}}^1}_{\text{place value}}+10\times\underbrace{\boldsymbol{\color{#333FB1}{16}}^0}_{\text{place value}}\\&=12\times\boldsymbol{\color{#333FB1}{16}}+10\times\boldsymbol{\color{#333FB1}{1}}\\&=192+10\\&=202_{10}\ \text{is its decimal value}\end{align}||
To better illustrate this conversion, here is the same character using binary and hexadecimal codes: ||\begin{align}&\text{Binary code}&&\text{Hexadecimal code}&&\text{Character}\\&11001010&&CA&&\text{É}\end{align}||As a result, the codes are easier to read and create.
Using the place value positions of each base, it is possible to write the same number in two different bases.
Since the decimal system is used universally, this system will be used as a reference.
From Base 10 to Another Base
How can we write 345 in base 12?
-
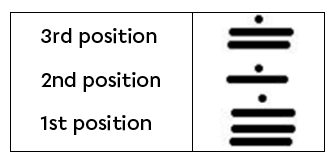
Determine the place value position of the identified base.
||\begin{align}1^\text{st}\ \text{position}_{\boldsymbol{\color{#333FB1}{12}}}&=12^0=1\\2^\text{nd}\ \text{position}_{\boldsymbol{\color{#333FB1}{12}}}&=12^1=12\\3^\text{rd}\ \text{position}_{\boldsymbol{\color{#333FB1}{12}}}&=12^2=144\\4^\text{th}\ \text{position}_{\boldsymbol{\color{#333FB1}{12}}}&=12^3=1728\end{align}||
-
Subtract, starting with the largest possible position.
||\begin{align}&345-(144+144)&&3^\text{rd}\ \text{place}\\ \Rightarrow\ &57-(12+12+12+12)&&2^\text{nd}\ \text{place}\\\Rightarrow\ &9-(1+1+1+1+1+1+1+1+1)&&1^\text{st}\ \text{place}\end{align}||
-
Match a quantity to each position.
||\begin{align}345_{10}&=\underbrace{144 + 144}_{3^\text{rd}\ \text{place}}+\underbrace{12+12+12+12}_{2^\text{nd}\ \text{place}}+\underbrace{1+1+1+1+1+1+1+1+1}_{1^\text{st}\ \text{place}}\\&=2\times\underbrace{144 }_{\text{place value}}+4\times\underbrace{12}_{\text{place value}}+9\times\underbrace{1}_{\text{place value}}\\&=2\times\underbrace{\boldsymbol{\color{#333FB1}{12}}^2}_{\text{place value}}+4\times\underbrace{\boldsymbol{\color{#333FB1}{12}}^1}_{\text{place value}}+9\times\underbrace{\boldsymbol{\color{#333FB1}{12}}^0}_{\text{place value}}\\&=249_{\boldsymbol{\color{#333FB1}{12}}}\end{align}||
The opposite method can also be used.
Converting From Any Base to Base 10
How can we write |{346_8}| in base 10?
-
Expand according to the value of each place.
||346_\boldsymbol{\color{#333FB1}{8}}=3\times\boldsymbol{\color{#333FB1}{8}}^2+4\times\boldsymbol{\color{#333FB1}{8}}^1+6\times\boldsymbol{\color{#333FB1}{8}}^0||
-
Calculate the total.
||\begin{alignat}{13}&=3\times64&&+4\times8&&+6\times1\\&=192&&+32&&+6\\&=230_{\boldsymbol{\color{#333FB1}{10}}}\end{alignat}||
Here are the symbols used to change from writing in base |10| to writing in base |12:|
|0,| |1,| |2,| |3,| |4,| |5,| |6,| |7,| |8,| |9,| |A| and |B.|
Here, |A| stands for “ten” and |B| for “eleven.”
For example, to write |22_{10}| in base |12,| |22_{10}| becomes |1A| in base |12.| ||\begin{align}22_{10}&=1\times12^1+10\times12^0\\&=1A_{12}\ \text{(1 dozen and 10 ones)}\end{align}||