Un système de numération est un ensemble de symboles (les chiffres) qui sont assemblés en suivant des règles d’écriture précises permettant d’écrire, de lire et d’énoncer les nombres.
Dans l’Histoire, des dizaines de systèmes de numération ont été inventés pour répondre à différents besoins. Il existe des systèmes de numération additive tels que les chiffres romains et des systèmes de position comme la numération décimale (base 10) qu’on utilise dans la vie de tous les jours. Depuis l’avènement des circuits électroniques et de l’informatique, les systèmes binaires (base 2) et hexadécimaux (base 16), qui sont également des systèmes de position, sont devenus indispensables. Mais, au juste, qu'est-ce qu'une base?
Une base, dans un système de numération positionnel, est le nombre de symboles (de chiffres) qui sont utilisés pour représenter les nombres.
En base |10| (la numération décimale), on utilise donc |10| chiffres, soit de |0| à |9|, tandis qu'en base |2| (la numération binaire), on n'utilise que |2| chiffres, c'est-à-dire le zéro |(0)| et le un |(1)|.
L'écriture des nombres comme on la connait utilise les chiffres indo-arabes, soit |0, \ 1, \ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9|. En théorie, cette écriture s'applique seulement à l'écriture en base |10| des nombres.
Or, pour faciliter la compréhension, ces mêmes chiffres seront utilisés tout au long de la fiche. Pour faire une différence au niveau de la base utilisée, on utilisera l'indice comme référence.
||576_{\color{blue}{12}} = 576 \ \small\text{en base} \ \color{blue}{12}||
Comme les formes d'écriture étaient très diversifiées vers |3500| av JC, les humains de cette époque devaient utiliser les moyens à leur disposition pour compter. Dans le cas présent, ils ont utilisé les doigts de la main gauche (5) et les phalanges de la main droite (12). Ainsi, 1 doigt de la main gauche était associé au groupe de 12 phalanges de la main droite.
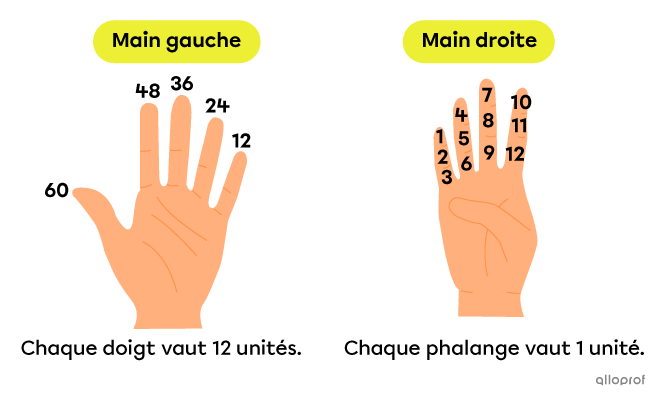
Source : Ifrah, G. (1994). Histoire universelle des chiffres. Éditions Robert Laffont.
Par exemple,
||\begin{align} \small\text{index gauche levé} + \small{1^{\small\text{re}} \ \text{phalange de l'index droit}}&= 4 \times \underbrace{\color{blue}{12}^1}_{\small\text{valeur de position}} + 10 \times\underbrace{\color{blue}{12}^0}_{\small\text{valeur de position}}\\
&=4 \times\color{blue}{12}+ 10 \times\color{blue}{1} \\
&= 48 + 10 \\
&= 58 \end{align}||Tout comme la numérotation en base |10|, on peut utiliser le système des valeurs des positions et la forme développée des nombres pour bien interpréter la valeur d'un nombre en base |12|.
Ainsi, cette façon de quantifier avec les doigts et les phalanges a fait apparaitre le système duodécimal, soit en base |12.|
Par ailleurs, cette façon de compter avec les doigts et les phalanges est également en lien avec le système sexagésimal, soit en base |60|.
En considérant les |5| doigts de la main gauche et les |12| phalanges de la main droite, on obtient un total de |60| possibilités. |\small{(5 \times 12 =60)}|
En ce qui concerne notre société contemporaine, cette base est présente dans nos unités de temps, soit les secondes, les minutes et les heures.
Combien y a-t-il de secondes dans 5 heures 17 minutes et 34 secondes?
||\begin{align} (\small 5\ \small\text{h}\ 17\ \small\text{min} \ 34 \ \small\text{sec})_{\color{blue}{60}} &= 5 \times\underbrace{\color{blue}{60}^2}_{\small\text{valeur de position}} + 17 \times\underbrace{\color{blue}{60}^1}_{\small\text{valeur de position}} + 34 \times\underbrace{\color{blue}{60}^0}_{\small\text{valeur de position}}\\
&=5 \times\color{blue}{60 \times60}+ 17 \times\color{blue}{60} + 34 \times\color{blue}{1} \\
&= 18 \ 000 + 1 \ 020 + 34 \\
&= 19 \ 054 \ \small\text{sec}\end{align}||
Par contre, cette méthode présentait un inconvénient de taille, soit la représentation des nombres avec une très grande valeur telle |5 \ 458 \ 384.| Pour pallier à cette difficulté, d'autres découvertes ont été faites dans les siècles suivants.
Lorsqu'est venu le temps de représenter de grandes quantités, l'utilisation de 10 doigts et de 2 mains ne suffisait plus. Ainsi, entre le XIV et XI siècle av JC, c'est en Chine qu'est apparu le système décimale, soit la base 10.
En fait, l'utilisation du 10 semblait évident pour eux puisqu'ils étaient habitués de dénombrer à l'aide de leurs 10 doigts. Par contre, l'apparition et l'utilisation officielle du 0 s'est fait attendre jusqu'au V siècle de notre ère.
Avec cette apparition de la valeur nulle est venue la notion de regrouper pour mieux représenter. Ainsi, un paquet de dix unités devenait une dizaine; un paquet de dix dizaines devenait une centaine et ainsi de suite.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Pour plus d'informations, les fiches sur <a href="/fr/eleves/bv/mathematiques/les-positions-et-les-valeurs-des-nombres-m1017">les valeurs de position</a> et <a href="/fr/eleves/bv/mathematiques/la-decomposition-des-nombres-m1018">la forme développée des nombres</a> sont disponibles sur la bibliothèque virtuelle.</p>
</body></html>
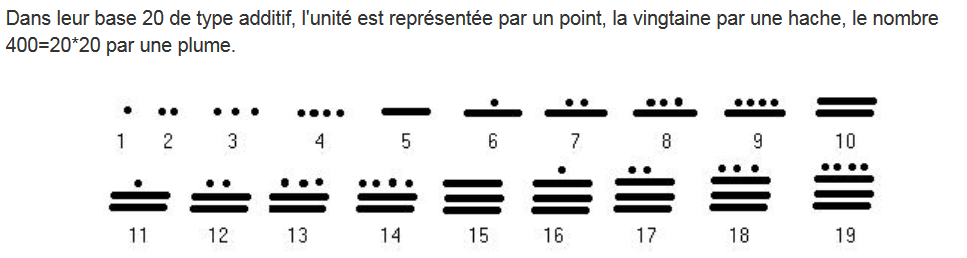
Toujours durant le V siècle, le peuple des Mayas a établi leur calendrier en utilisant une base 20. Pourquoi? Non seulement ils utilisaient leurs 10 doigts, mais également leurs 10 orteils!
Puisqu'il ne s'agit pas d'une base 10, les symboles utilisés pour représenter les différentes quantités ne sont pas les chiffres comme on les connait.
De plus, l'écriture des nombres par le biais de ce système ne se faisait pas de gauche à droite, mais du bas vers le haut.
Tout comme la numérotation en base 10, on peut utiliser le système des valeurs de position et la forme développée des nombres pour bien interpréter leur valeur respective.
En utilisant les chiffres tels qu'on les connait, détermine le nombre associé à cette illustration.
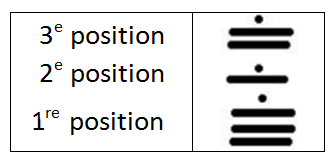
||\begin{align}\text{Ce nombre}_{\color{blue}{20}} &= 11 \times\underbrace{\color{blue}{20^2}}_{\small\text{valeur de position}} + 6 \times\underbrace{\color{blue}{20}^1}_{\small\text{valeur de position}} + 16 \times\underbrace{\color{blue}{20}^0}_{\small\text{valeur de position}}\\
&=11 \times\color{blue}{20\times20}+ 6 \times\color{blue}{20} + 16 \times\color{blue}{1} \\
&= 4 \ 400 + 120 + 16\\
&= 4 \ 536_{10} \ \text{est sa valeur décimale} \end{align}||
Contrairement aux autres bases, le système binaire, soit en base 2, est assez récent. Même si sa découverte a été réalisée vers la fin du XVII siècle, c'est surtout depuis le début du XX siècle qu'il est pleinement exploité.
En fait, cette manière de coder les informations est la seule qui peut être comprise par les diverses composantes électroniques d'un ordinateur. Généralement associé aux bits (de l'anglais binary digit), ce code n'est composé que de deux symboles: 0 et 1.
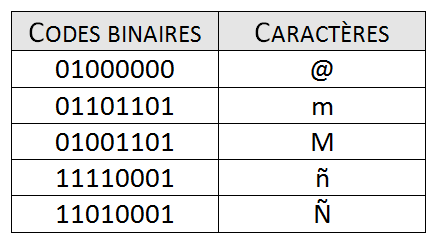
Pour standardiser le codage informatique, ces bits ont été regroupés par 8 pour former des octets. Ainsi, chaque octet est associé à un chiffre, une lettre, une ponctuation, un accent, etc. Bref, chaque octet est associé à un caractère précis de l'alphabet latin. Voici un aperçu de la table des caractères utilisés par le code ISO/CEI 8859-1, soit "l'alphabet informatique" selon le codage par octet.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Tout comme la numérotation en base 10, on peut utiliser le système <a href="/fr/eleves/bv/mathematiques/les-positions-et-les-valeurs-des-nombres-m1017">des valeurs de position</a> et <a href="/fr/eleves/bv/mathematiques/la-decomposition-des-nombres-m1018">la forme développée des nombres</a> pour bien interpréter leur valeur respective. </p>
</body></html>
Puisque chaque caractère possède un octet qui lui est unique, on peut en déduire une valeur décimale. Par ailleurs, cette valeur décimale est souvent associée à des touches raccourcies universelles.
Quelle est la valeur décimale de ce caractère?
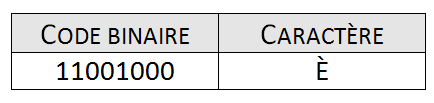
||\begin{align} 11001000_{\color{blue}{2}} &= 1 \times\underbrace{\color{blue}{2^7}}_{\small\text{valeur de position}} + 1 \times\underbrace{\color{blue}{2}^6}_{\small\text{valeur de position}} + 1 \times\underbrace{\color{blue}{2}^3}_{\small\text{valeur de position}}\\
&=1 \times\color{blue}{2\times2 \times2 \times2 \times2 \times2 \times2}+ 1 \times\color{blue}{2 \times2 \times2 \times2 \times2 \times2} + 1 \times\color{blue}{2 \times2 \times2} \\
&= 128 + 64+ 8\\
&= 200_{10} \ \text{est sa valeur décimale}\end{align}||
Fait à noter, les |0| ont volontairement été éliminés des calculs puisque leur valeur nulle n'affecte en rien la réponse finale.
Par contre, avec ces interminables suites de |0| et de |1|, il peut être facile de se tromper. Dans ce cas, on n'obtient pas le caractère que l'on désire et on doit vérifier le code en entier pour trouver son erreur. Pour pallier à cette difficulté, la base |16| a été introduite au langage informatique.
Par définition, tous les nombres de |0| à |15| inclusivement pouvaient être utilisés pour former le code hexadécimal. Par ailleurs, cela présentait un problème puisqu'il ne pouvait y avoir qu'un caractère par position. Ainsi, la nomenclature suivante a été adoptée.||\begin{align} 0 &= 0 &4 &= 4 & 8 &= 8 & 12 &=C\\1&=1 &5 &=5 & 9 &= 9 & 13&=D \\2&=2 &6 &=6 &10 &= A & 14 &= E \\ 3 &= 3 & 7 &=7 & 11&= B & 15&= F \end{align}||Alors, quelle est la valeur décimale de ce caractère?

||\begin{align}\text{CA}_{\color{blue}{16}} &= C\times\underbrace{\color{blue}{16^1}}_{\small\text{valeur de position}} + A \times\underbrace{\color{blue}{16}^0}_{\small\text{valeur de position}}\\ &= 12 \times\underbrace{\color{blue}{16^1}}_{\small\text{valeur de position}} + 10 \times\underbrace{\color{blue}{16}^0}_{\small\text{valeur de position}}\\
&=12 \times\color{blue}{16}+ 10 \times\color{blue}{1} \\
&= 192 + 10\\
&= 202_{10} \ \text{est sa valeur décimale}\end{align}||
Pour avoir une meilleure représentation d'un tel changement, voici le même caractère avec les codes binaire et hexadécimal:
||\begin{align} &\small\text{code binaire} && \small\text{code hexadécimal} && \small\text{caractère} \\
&11001010 && CA && \text{É} \end{align}||
Ainsi, les codes deviennent plus légers et donc plus faciles à lire et à créer.
Grâce aux valeurs de position qui sont présentes dans chacune des bases, il est possible d'écrire un même nombre sous deux bases différentes.
Puisque le système décimale est utilisé de manière universelle, c'est ce système qui sera utilisé comme référence.
De la base 10 vers une autre base
Comment écrit-on 345 en base 12?
- Déterminer la valeur des positions de la base identifiée ||\begin{align} 1^\text{re} \ \text{position}_{\color{blue}{12}} &= 12^0 = 1 \\2^\text{e} \ \text{position}_{\color{blue}{12}} &= 12^1 = 12 \\3^\text{e} \ \text{position}_{\color{blue}{12}} &= 12^2 = 144 \\4^\text{e} \ \text{position}_{\color{blue}{12}} &= 12^3 = 1 \ 728 \\\end{align}||
- Procéder par soustraction en commençant par la plus grande position possible ||\begin{align} &345 - (144 + 144) && 3^e \ \text{position}\\ \Rightarrow &57 - (12 + 12 + 12 + 12) && 2^e \ \text{position}\\ \Rightarrow &9 - (1+1+1+1+1+1+1+1+1) && 1^{ère} \ \text{position}\end{align}||
- Associer une quantité à chaque position ||\begin{align} 345_{10}&=\underbrace{144 + 144}_{3^\text{e} \ \text{position}} + \underbrace{12+12+12+12}_{2^\text{e} \ \text{position}} + \underbrace{1+1+1+1+1+1+1+1+1}_{1^\text{re} \ \text{position}} \\ &=2 \times \underbrace{144 }_{\text{valeur de position}} + 4 \times \underbrace{12}_{\text{valeur de position}} + 9 \times \underbrace{1}_{\text{valeur de position}} \\ &=2 \times \underbrace{\color{blue}{12}^2}_{\text{valeur de position}} + 4 \times \underbrace{\color{blue}{12}^1}_{\text{valeur de position}} +9 \times \underbrace{\color{blue}{12}^0}_{\text{valeur de position}} \\ &=249_{\color{blue}{12}} \end{align}||
On peut également faire le chemin inverse.
Passage d'une base quelconque vers la base 10
Comment écrit-on |{346_8}| en base 10?
-
Développer selon la valeur de chacune des positions ||346_\color{blue}{8}=3\times \color{blue}{8}^2+4\times \color{blue}{8}^1+6\times \color{blue}{8}^0||
-
Calculer le total ||\begin{align}\phantom{346-\color{blue}{8}} &= 3 \times 64 &+ &4 \times 8 &+ &6 \times 1 \\ &= 192 &+ &32 &+ &6 \\ &= 230_{\color{blue}{10}} \end{align}||
Voici les symboles utilisés pour le passage de l'écriture de la base |10| vers l'écriture de la base |12:|
|0,| |1,| |2,| |3,| |4,| |5,| |6,| |7,| |8,| |9,| |A| et |B|
Ici, on écrit |A| pour désigner « dix » et |B| pour désigner « onze ».
Par exemple, si on veut écrire |22_{10}| en base |12|, alors |22_{10}| deviendrait |1A| en base |12.| ||\begin{align} 22_{10} &= 1 \times12^1 + 10 \times12^0\\
&= 1A_{12} \ \text{(une douzaine et 10 unités)} \end{align}||