To meet different needs, it is possible that one solid is not enough. In this case, it may be necessary to combine several solids or to alter one.
A decomposable solid is a solid that can be separated into several simpler solids.
As the definition states, it is simply a matter of recognizing the various solids used in its construction.
In summary, a decomposable solid must have the following characteristics:
-
It must be formed using at least two solids.
-
The solids used must have a common face or a common section of a face.
-
It can be made of both polyhedra and curved surfaces.
With these characteristics, the possible combinations when building a decomposable solid are unlimited.
It becomes easier to calculate area and volume by recognizing the different solids used. New solids can be created not only by adding solids but also by removing sections of them.
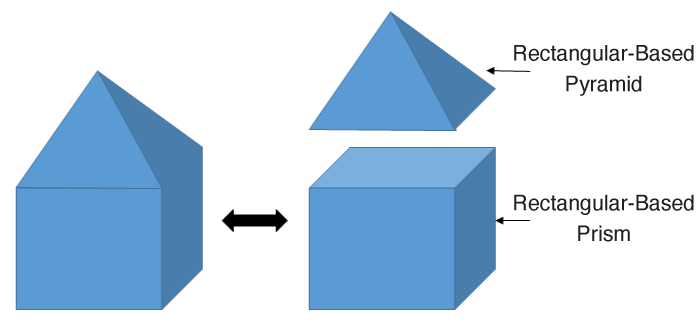
A stack of wooden blocks (left) corresponds to a decomposable solid. The solid on the right is formed by the combination of a pyramid and a prism.
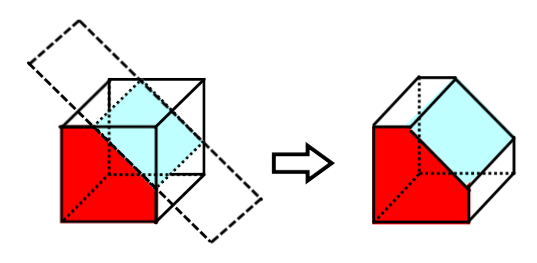
A truncated solid is a solid that has been cut by a plane and has only a portion of the separated sections remaining.
In this case, the expression "a picture is worth a thousand words" takes on its full meaning. Instead of listing the different construction characteristics of these solids, here are some examples.
Polyhedron Truncated by a Single Plane
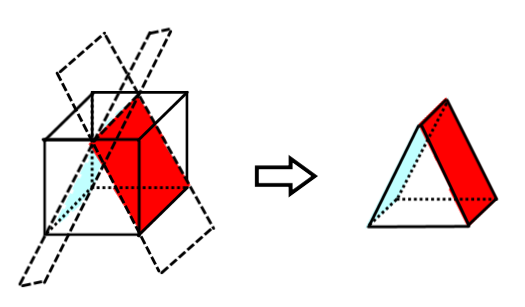
Polyhedron Truncated by Several Planes
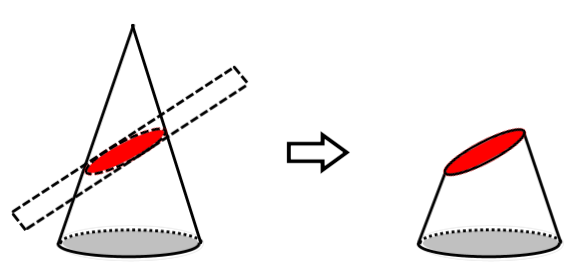
Curved Surface Truncated by a Plane
Curved Surface Truncated by Several Planes
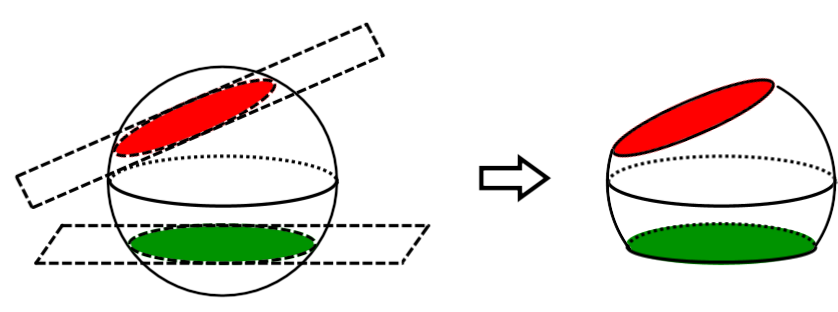
Some truncated solids have specific names and characteristics, such as the triangular prism (second drawing). For others, addition and subtraction can be used to combine different formulas to calculate their area and volume.
Be careful not to confuse a truncated solid with a non-convex solid. There is a difference between cutting a solid by a plane and removing a portion of a solid from its interior.
