It is possible to draw or recognize geometric figures according to their characteristics. Some polygons, like the line, are one-dimensional. Others, like the rectangle, are defined in two-dimensional space (with a width and a length). Finally, solids, like the cube or sphere, are three-dimensional geometric figures. They have length, width, and depth (height). In all these cases, geometric figures refer to a set of points in the space of dimensions which are given and defined.
Note that the point is a geometric figure without dimension since it has neither length, width, nor depth. It is also the only geometric figure to belong to dimension |0.|
Two-dimensional geometric figures are also called plane figures.
A plane figure, formed with straight or curved lines, is a two-dimensional geometric figure whose points are all located on the same plane.
Among plane figures, it is important to distinguish between polygons and non-polygons.
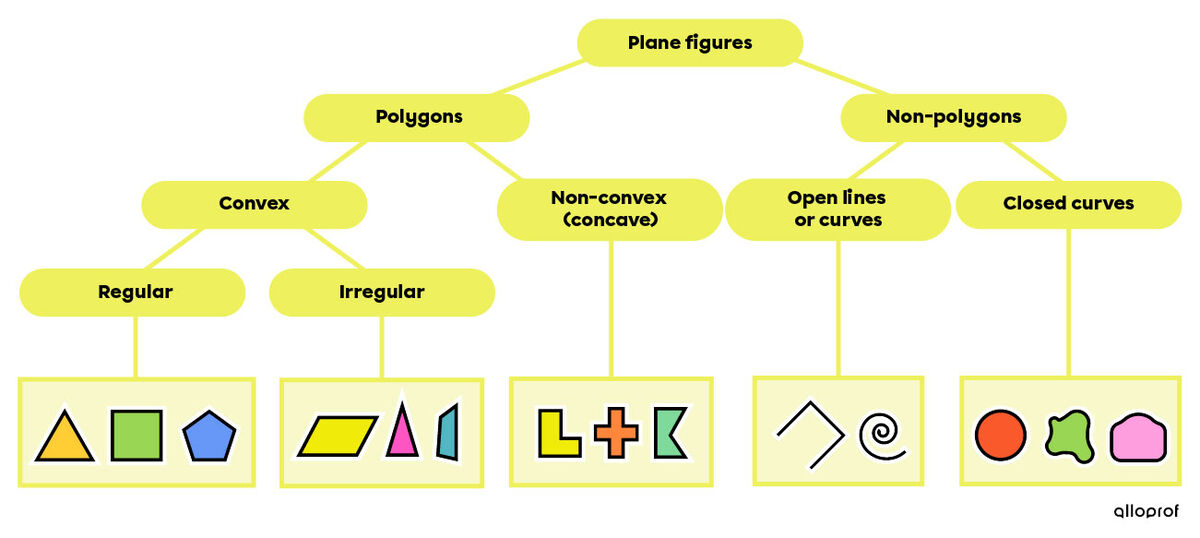
A polygon is a closed plane figure that is formed by line segments joined end-to-end.
Non-polygons define the set of plane figures which have curved lines or which include unclosed lines.
The prefix poly- comes from the Greek -polus, which means many, and the suffix -gone comes from the Greek -gônia, which means angle. So, polygons have several angles, and they must not contain curved lines. To understand the terminology associated with polygons, a vertex, a side, and a surface must be defined clearly.
|
Concept |
Definition |
Example |
|---|---|---|
|
Vertex |
The vertex is the point at which two lines meet. The vertices are named by uppercase letters which are assigned to them arbitrarily. |
This rhombus has four vertices: |A|, |B|, |C| and |D|. |
|
Side |
The side of a polygon is a line segment that forms one of its borders. A side is named by the two letters of the vertices it connects (e.g.: |\overline{AB}|). |
Sides |\overline{AB}, \overline{BC}| and |\overline {AC}| form the triangle below. |
|
Surface |
A plane surface is the flat surface of the polygon bounded by its sides. |
Sides |\overline{AB}, \overline{BC}| and |\overline {AC}| form the plane occupied by triangle ABC.
|