Expressing the perimeter and area of polygons using variables involves representing the perimeter or area using an algebraic expression.
The algebraic method is used to express the perimeter or a figure’s area when numerical values are missing from the measurements. Thus, if a numeric value cannot be used, a variable will replace the unknown values.
Using algebraic expressions and variables makes it possible to generalize about the desired measurement. In the case of a perimeter, the algebraic expression makes it possible to evaluate the perimeter by substituting a variable with a precise value. This avoids having to redo the calculations each time.
If the rectangle’s length is three times its width,
a) What is the algebraic expression associated with its perimeter?
b) What is its perimeter if the width is 10 cm?
c) What is its perimeter if the width is 4.7 cm?
-
Make a drawing and write the variables/algebraic expressions
|\begin{align*}
x &= \text{Width of rectangle}\\
3x &= \text{Length of rectangle}\end{align*}|
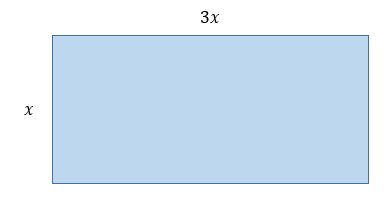
-
Find the algebraic expression associated with the perimeter (question a))
|\begin{align*}
P_\text{rectangle} &= 2\times \text{width} + 2\times \text{length} \\
&= 2 (x) + 2 (3x) \\
&= 2x + 6x \\
&= 8x
\end{align*}| -
Evaluate the algebraic expression according to the given value
b) If the width is 10 cm:|\begin{align*}
P_\text{rectangle} &= 8x \\
&= 8 (10) \\
&= 80\ \text{cm}
\end{align*}|c) If the width is 4.7 cm:
|\begin{align*}
P_\text{rectangle} &= 8x \\
&= 8 (4.7) \\
&= 37.6\ \text{cm}
\end{align*}|
To learn more about algebraic representation of a regular polygon’s perimeter, see the concept sheet: The Perimeter of a Regular Polygon Expressed Using Variables.
A plane figure can be assigned an algebraic expression as it's value. The representation is used when the numerical values are unknown. Thus, they are replaced by algebraic expressions.
If a triangle’s height is half of its base,
a) What is the algebraic expression associated with its area?
b) What is its area if its base measures 12.5 cm?
-
Make a drawing and write the variables/algebraic expressions
|\begin{align*}
x &= \text{measurement of the triangle’s base} \\ \\
\frac{x}{2} &= \text{measurement of the triangle’s height}
\end{align*}|
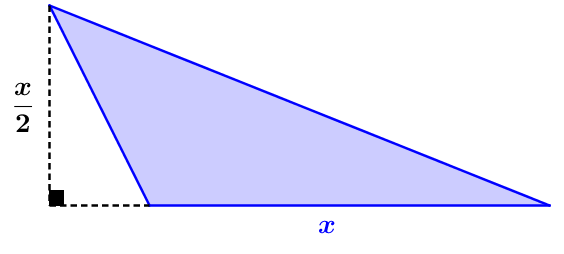
-
Find the algebraic expression associated with the area (question a))
|\begin{align*}
A_\text{triangle} &= \frac{\text{base} \times \text{height}}{2} \\ \\
&=\dfrac{x \left(\frac{x}{2}\right)}{2} \\ \\
&= \frac{\frac{x^2}{2}}{2} \\ \\
&= \frac{x^2}{4}
\end{align*}| -
Evaluate the algebraic expression according to the given value
b) If the base is 12.5 cm?
|\begin{align*}
A_\text{triangle} &= \frac{x^2}{4} \\ \\
&= \frac{12.5^2}{4} \\ \\
&\approx 39.06 \ \text{cm}^2
\end{align*}|
To learn more about using algebraic expressions and a regular polygon’s area, consult the concept sheet: The Area of a Regular Polygon Expressed Using a Variable.