As its name suggests, a reflection is the result of an initial figure whose reflection is constructed by a mirror.
A Reflection, or symmetry, is a geometric transformation that produces a “mirror” image of the initial figure with respect to a line called the axis of reflection.
The axis of reflection, generally denoted |s,| is the perpendicular bisector of the segments that connects corresponding vertices. In other words, the axis of reflection has the following properties:
-
The corresponding points of the initial figure and the image figure are equidistant from the axis of reflection.
-
The segments that connect corresponding vertices are perpendicular to the axis of reflection.
The image figure |A'B'C'D'E'| is a reflection of the initial figure |ABCDE| with respect to the axis of reflection.
Reflection is a geometric transformation that generates isometric figures and is therefore considered a type of isometry, just like rotation and translation.
To distinguish between the corresponding points in the initial figure and the image figure, we use the ‘’ ' ‘’ symbol (called prime). Vertex A in the initial figure becomes vertex A' in the image figure.
Due to their properties, it is important not to confuse the “axis of reflection” and the “axis of symmetry.”
An axis of symmetry, or line of symmetry, is a line that divides a figure into two congruent parts.
Here is an illustration of the difference between axes of symmetry and reflection:

The axis of symmetry separates triangle ABC into 2 equal parts. The axis of reflection produces an exact copy of triangle ABC.
The properties of reflections can be used to verify if an image has been generated from a rotation, or to demonstrate the construction of a reflected image.
| Properties of a reflection | Example |
|---|---|
|
The corresponding sides of an initial figure and its image are not necessarily parallel. |
|\overline{AB} \not\parallel \overline{A'B'}, \overline{BC} \not\parallel \overline{B'C'}, \overline{CD} \not\parallel \overline{C'D'} \text{ and } \overline{AD} \not\parallel \overline{A'D'}|
|
|
The orientation of the corresponding vertices are placed in reverse order. |
|
|
The line segments drawn to connect the corresponding vertices are parallel, but they are not necessarily isometric. |
|\overline{AA'} \parallel \overline{BB'} \parallel \overline{CC'} \parallel \overline{DD'}| |m\overline{AA'} \neq m\overline{BB'} \neq m\overline{CC'} \neq m\overline{DD'}|
|
The image of a reflected figure can be constructed by following these steps:
-
Using a ruler and a set square, draw lines that are perpendicular to the axis of reflection |s| through each of the vertices of the figure.
-
Use a ruler or open a compass to the length between one vertex and the axis of reflection |s.|
-
Use a ruler or place the needle point of the compass on the point where the axis of reflection meets the perpendicular line coming from the vertex. Mark the compass measurement on the perpendicular line on the opposite side of the axis of reflection by drawing a small arc.
-
Repeat steps 2 and 3 for each vertex on the figure.
-
Using a ruler, connect the points obtained to draw the image of the initial figure while labelling the resulting image points using the prime symbol (').
To construct the image figure of the polygon below using a reflection, follow these steps:
|
1. Using a ruler and a set square, draw lines that are perpendicular to the axis of reflection |s| through each of the vertices of the figure.
|
2. Use a ruler or open the compass to the length between one vertex and the axis of reflection |s.|
|
|
3. Use a ruler or place the needle point of the compass on the point where the axis of reflection meets the perpendicular line coming from the vertex. Mark the compass measurement on the perpendicular line on the opposite side of the axis of reflection by drawing a small arc.
|
4. Repeat steps 2 and 3 for each vertex on the figure.
|
|
5. Using a ruler, connect the points obtained to draw the image of the initial figure while labelling the resulting image points using the prime symbol (').
|
|
Sometimes, the axis of reflection may be located inside the initial figure itself. Despite this, the steps to follow are the same.
|
Step 1
|
Step 2
|
|
Step 3
|
Step 4
|
|
Step 5
|
|
1) Identify the image figure and the initial figure.
The image figure is the one whose vertices are identified with the prime symbol ('). Here, the image figure is the green triangle and the initial figure is the purple triangle.
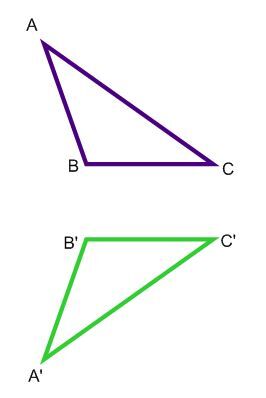
2) Use segments to connect each pair of corresponding vertices.
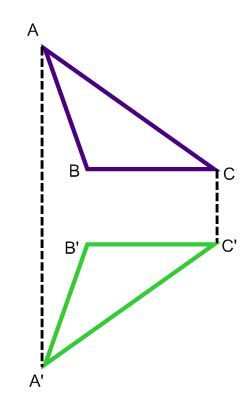
3) Mark the midpoint of each segment drawn in Step 2.
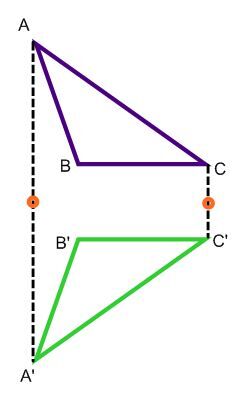
4) Draw the line that passes through the midpoints found in Step 3.
