A rotation is a geometric transformation that turns a figure about a fixed point, called the centre of rotation, according to an angle. In other words, a rotation |r| is defined by its centre |O| and its angle |\theta.| A rotation is denoted as: |r_{(O, \theta)}.|
Some specific rotations can be defined by the following rules when they are centred at the origin |O=(0,0)|:
|r_{(O,90°)}| or |r_{(O,-270°)}: (x, y) \mapsto (-y, x)| for a rotation of |90°| or |-270°.|
|r_{(O,180°)}| or |r_{(O,-180°)}: (x, y) \mapsto (-x, -y)| for a rotation of |180°| or |-180°.|
|r_{(O,270°)}| or |r_{(O,-90°)}: (x, y) \mapsto (y, -x)| for a rotation of |270°| or |-90°.|
|x| and |y| are the coordinates of the point being rotated.
Rotations of |180°| and |-180°| are equivalent. They both move the initial figure one half of a full revolution about the origin. This is why they have the same rotation rule.
A rotation’s positive direction follows the opposite direction of the hands of a clock (counterclockwise).
A rotation of |90°| means a rotation of |90°| counterclockwise (from noon to 9 o’clock, for example).
On the other hand, a rotation of |-90°| means a rotation of |90°| clockwise (from noon to 3 o’clock, for example).
Why do we turn counterclockwise when we rotate in a positive direction?
The positive and negative directions are related to the numbering of the quadrants. The quadrants are numbered in a counterclockwise direction as well. Rotating in the same direction as the quadrant numbering implies rotating in a positive direction.
Rotate clockwise by |90°,| centred at the origin in a clockwise direction.
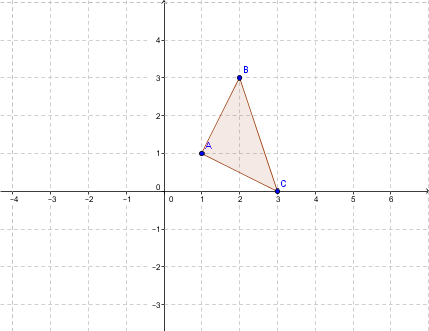
Step 1: Properly identify the rotation information.
Centre: |(0, 0)|
Magnitude: |90°|
Direction: clockwise
This is a rotation of |-90°| (the negative sign means clockwise direction). The rule corresponding to this rotation is the following: |r_{(O, -90°)}:(x,y)\mapsto (y,-x).|
Step 2: Identify the vertices of the initial figure.
|A (1, 1)|
|B (2, 3)|
|C (3, 0)|
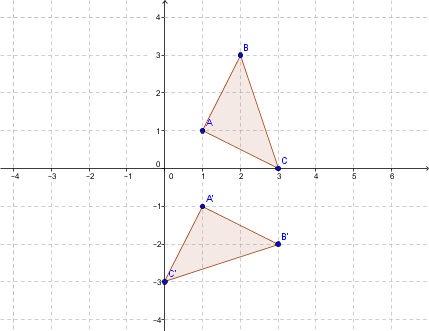
Step 3: Using the rotation rule, find the coordinates of the vertices of the image figure.
The rule states that the y-coordinate of the initial figure becomes the x-coordinate of the image figure (final figure). Next, the x-coordinate of the initial figure must switch signs and become the y-coordinate of the image figure.
|A (1, 1) \mapsto (1, -1) = A’|
|B (2, 3) \mapsto (3, -2) = B’|
|C (3, 0) \mapsto (0, -3) = C’|
Step 4: The new coordinates are the vertices of the image of the initial figure after rotating by |-90°.|
Graph the image triangle.
The following image illustrates the |90°| clockwise displacement of each point about the centre:
If the centre of rotation is not at the origin:
The figure must be first translated to bring the centre of rotation to the origin of the Cartesian plane. The translation applies to all of the vertices of the initial figure.
It is then rotated according to the rule.
Lastly, the inverse translation is performed. If translation |t_{(a,b)}| is performed first, then translation |t_{(-a,-b)}| must be performed last.
Rotate triangle |ABC| by a counterclockwise angle of |90°| about point |(-1,2).|
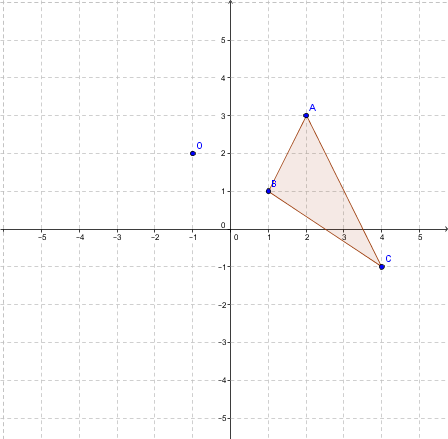
The vertices of the initial figure are:
|A(2,3)|
|B(1,1)|
|C(4,-1)|
Each of these points must be translated to bring the centre of rotation to |(0,0).| The rule |t_{(1,-2)}:(x,y) \mapsto (x+1,y-2)| is obtained.
The new points are:
|A(2,3) \mapsto (3,1)=A'|
|B(1,1) \mapsto (2,-1)=B'|
|C(4,-1) \mapsto (5,-3)=C'|
The red figure is obtained.
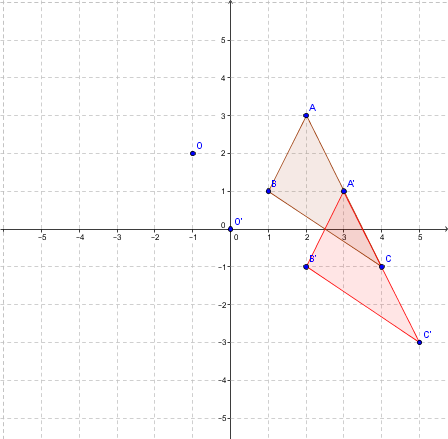
Rotate the triangle by a counterclockwise angle of |90°| about centre |O’.|
Use the rule |r_{(O,90°)}:(x,y) \mapsto (-y,x).|
This gives the points:
|A'(3,1) \mapsto (-1,3)=A''|
|B'(2,-1) \mapsto (1,2)=B''|
|C'(5,-3) \mapsto (3,5)=C''|
The blue figure is obtained.
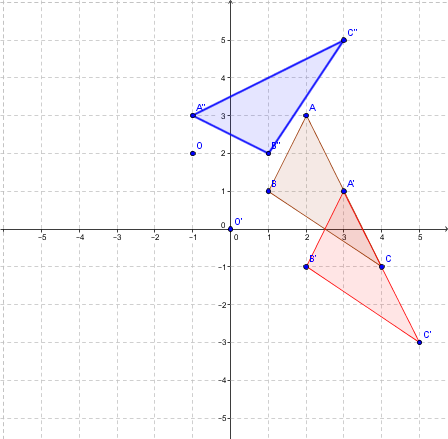
The last step is to perform the inverse translation, specifically |t_{(-1,2)}:(x,y) \mapsto (x-1,y+2).|
This gives the points:
|A''(-1,3) \mapsto (-2,5)=A'''|
|B''(1,2) \mapsto (0,4)=B'''|
|C''(3,5) \mapsto (2,7)=C'''|
The final outcome is the pink triangle.
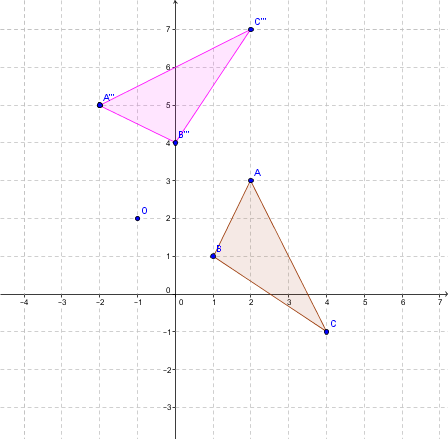
Example of a Rotation
The pink triangle is the initial figure.

Compare the coordinates of the corresponding vertices:
|A| and |A’|: |(2, 3)| and |(-3, 2)|
|B| and |B’|: |(3, 2)| and |(-2, 3)|
|C| and |C’|: |(1, 1)| and |( -1, 1)|
Notice that the order of the coordinates was reversed and that the original y-coordinate changed signs: |(x, y) \mapsto (-y, x).|
These changes correspond to those of a rotation of |90°| or |-270°.|
BE CAREFUL: Looking at the diagram, it ressembles a reflection with respect to the y-axis, but this is not the case. It is very important to correctly identify the corresponding vertices.